Outcome Variation in the Social Security Disability Insurance Program: The Role of Primary Diagnoses
Social Security Bulletin, Vol. 73, No. 2, 2013
Based on the adjudicative process, the author classifies claimant-level data over an 8-year period (1997–2004) into four mutually exclusive categories: (1) initial allowances, (2) initial denials not appealed, (3) final allowances, and (4) final denials. The ability to predict those outcomes is explored within a multilevel modeling framework, with applicants clustered by state and primary diagnosis code. Variance decomposition suggests that medical diagnoses play a substantial role in explaining individual-level variation in initial allowances. Moreover, there is statistically significant high positive correlation between the predictions of an initial allowance and a final allowance across the diagnoses. This finding suggests that the ordinal ranking of impairments between these two adjudicative outcomes is widely preserved. In other words, impairments with a higher expectation of an initial allowance also tend to have a higher expectation of a final allowance.
Javier Meseguer is an economist with the Office of Economic Analysis and Comparative Studies, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Introduction
| ALJ | administrative law judge |
| DDS | Disability Determination Service |
| DI | Disability Insurance |
| DIC | deviance information criterion |
| DRF | Disability Research File |
| RFC | residual functional capacity |
| SGA | substantial gainful activity |
| SSA | Social Security Administration |
| SSI | Supplemental Security Income |
The purpose of the Disability Insurance (DI) program is to replace part of a worker's earnings in the eventuality of a physical or mental impairment preventing the individual from working. The disability portion of the Old-Age, Survivors, and Disability Insurance (OASDI) program, administered by the Social Security Administration (SSA), protects workers and their eligible dependents against such risk. SSA administers a second program, Supplemental Security Income (SSI), which has no employment or contribution requirements, but imposes strict income and asset limits. It is designed to be a program of last resort, assisting aged, blind, or disabled individuals who have very limited resources.
The goal of this study is to explore the extent to which medical diagnoses and state of origin may explain observed heterogeneity in disability decisions. One instance of heterogeneity is manifest at the state level. The DI program is federally administered and is operated in collaboration with the states. When a local Social Security field office establishes that an applicant meets all of his or her nonmedical requirements, the case is forwarded to the state Disability Determination Service (DDS) for a decision. The DDS follows a sequential process to evaluate the medical evidence and decide if the applicant meets the definition of disability. In doing so, a DDS examiner considers the severity of the impairment(s), along with vocational factors that take into account age, education, and work experience. SSA guidelines to determine disability are uniform across all 50 states. In practice, however, there can be wide variation in state allowance rates.
A second instance of variation in DI outcomes occurs through the adjudicative process. If a disability claim is denied, the applicant has a number of opportunities to appeal the decision. There are three stages of appeal within SSA: (1) a reconsideration by the state DDS, (2) a hearing before an administrative law judge (ALJ), and (3) a review by the Appeals Council. If those stages are exhausted, the claimant can always seek legal redress in a federal district court. While few initial denials are reversed at the reconsideration level, a substantial portion of claimants who appeal at the hearing level or above are eventually allowed.
The two referenced sources of variation in disability outcomes (by state and adjudicative level) have been a cause of concern to SSA and Congress regarding the practical implementation of the disability programs. My hunch is that the collection of impairments in particular might shed some light in explaining a portion of the observed variation. Thus, I investigate heterogeneity in disability outcomes along three dimensions: state of origin, medical diagnosis, and adjudicative stage. That objective is pursued by working with a random sample of the Disability Research File (DRF). The DRF follows a cohort of applicants through the various stages of the determination process, identifying decisions made at different adjudicative levels. The disability determinations in the file are separated into four mutually exclusive categories: (1) initial allowances, (2) initial denials not appealed, (3) final allowances, and (4) final denials. This classification of the data implicitly reduces the adjudicative process to two stages (initial and final).
The data is fitted to various Bayesian hierarchical multinomial logit specifications, with two different groups or clusters nesting the claimant-level observations. One group is the 50 states. The other group comprises 181 medical impairments, which represent the unique administrative four-digit primary diagnosis codes. This modeling approach offers several advantages. First, the framework is multivariate, meaning that instead of estimating a separate model for each stage, the adjudicative outcomes are estimated jointly. Second, the multilevel or hierarchical nature of the models enables the distinction to be made between claimant-level effects on one hand and state or diagnosis-level effects on the other hand. In other words, I can decompose heterogeneity in the adjudicative outcomes by source into "between-group" and "within-group" variance. For instance, at one end of the spectrum, it is possible that claimants within a state are rather uniform in their characteristics, so that most of the variance in initial allowances is due to unique differences between the states. Alternatively, a large portion of the total variance could be attributed to claimant-level heterogeneity within the states (that is, the states are not that different from one another, but the population within a given state varies greatly in its characteristics). Finally, a third advantage in this modeling approach is the ability to estimate correlation patterns that may exist between the disability adjudicative outcomes.
The next section in this article provides background information about the Social Security disability programs, including the disability determination and appeals processes. I then briefly review some of the literature regarding the modeling of allowance rates. The data and modeling approach are discussed next, emphasizing the observed variation in adjudicative outcomes by such factors as age, diagnosis group, state of origin, and mortality. The inferential results are presented in the following section, where the "goodness-of-fit" of the various models and the "average effect" of various explanatory variables are evaluated and discussed. Two other important issues addressed in this section involve variance decomposition and correlation, where I describe the interpretation and implications of my estimates. The last section concludes with a summary of the main findings.
Social Security Disability Programs
SSA operates two different programs that offer cash benefits to the disabled: the Disability Insurance program, which was enacted in 1956, and the Supplemental Security Income program, which began in 1972. The two programs share the same disability determination process, but have different objectives. DI is funded through payroll tax contributions and is designed to protect workers contributing to the program from earnings losses that are due to impairment. SSI, on the other hand, is not contributory. General revenues fund it, and the main goal of the program is to guarantee a minimal level of income to the poorest of the aged, blind, or disabled population.
The DI program provides benefits to disabled workers who are younger than their respective full retirement ages and to their spouses, surviving disabled spouses, and disabled children, although workers account for the largest share of beneficiaries (typically, over 80 percent of the DI rolls). At the end of 2010, about 8.8 million workers and their dependents were receiving DI benefits and 4.7 million individuals were receiving SSI payments. Under both programs, the definition of disability is one of long-term work disability. It involves the inability to engage in substantial gainful activity (SGA) because of a medically determinable physical or mental impairment that is expected to last at least 12 months or result in death.
Eligibility for DI benefits requires a worker to be insured, younger than his or her full retirement age, and to meet the definition of disability. The applicant must have worked long enough in employment covered by Social Security (approximately 10 years) and recently enough (about 5 of the past 10 years). Those requirements are relaxed for younger applicants who have shorter employment histories. An applicant who is employed must also have monthly earnings below the SGA threshold ($1,640 for a blind person and $1,000 for a nonblind individual in 2010). However, there are no restrictions on nonwage income. Upon approval, benefits are received after a 5-month waiting period from the onset of disability. In addition, the beneficiary is entitled to Medicare coverage after receiving benefits for 2 years.
Disability benefits continue for as long as the beneficiary remains disabled or reaches full retirement age, in which case there is a conversion to retirement benefits. Upon death of a worker, some dependent benefits may convert into survivor benefits. SSA conducts periodic continuing disability reviews (CDRs) to determine if an individual remains disabled. Review frequency depends on the severity and likelihood of improvement of the disability and can range from 6 months from the initial finding to as long as 7 years. A finding that a beneficiary is engaging in SGA will result in termination.1
From 1970 through 2009, the number of beneficiaries in the DI program more than tripled, while DI expenditures increased by almost seven times in inflation-adjusted figures (Congressional Budget Office 2010). According to the Social Security Advisory Board (2012a), that expansion can be traced to several factors in addition to an increase in the general population. One factor has been an increase in the share of lower mortality impairments with earlier onset (such as musculoskeletal and mental disorders). Applicants with those types of impairments tend to enter the program at younger ages and remain as beneficiaries for longer periods of time. Another factor has been an increase in female labor force participation. The rapid pace at which women have joined the ranks among workers has considerably expanded the pool of applicants. Indeed, the gender composition of beneficiaries today is much closer to that of the population at large. A third factor has been an increase in earnings replacement rates. Rising income inequality coupled with the average wage indexing of benefits has increased the portion of potential earnings replaced by DI benefits. Younger low-skilled workers in particular have experienced the highest increase in the value of DI benefits at a time of reduced demand for their labor. Exacerbating the gap between potential earnings and disability benefits is a reduction in private health insurance coverage. Eventual access to Medicare after 2 years on the DI rolls may provide an additional enticement to apply.
The Sequential Disability Determination Process
A claimant typically files an application for DI or SSI in a Social Security field office. The field office gathers a variety of information from the applicant regarding entitlement status, impairment(s), and medical records. The disability determination follows a five-step sequential evaluation process that considers employment, medical, and vocational factors, in that order.
- Step 1: If the applicant is employed and earning more than the SGA amount, an SSA employee denies the claim. Otherwise, the field office sends the claim to the DDS.
- Step 2: If a medical impairment (or combination of impairments) is not severe enough to interfere with basic work-related activities for at least 1 year, a DDS examiner denies the claim. Otherwise, the evaluation proceeds to the next step.
- Step 3: Impairments that meet the criteria in SSA's medical listings or are found to be of equal severity result in an allowance determination. Otherwise, the claim is referred to the next step.
- Step 4: An applicant found with the capacity to engage in relevant employment performed in the past is denied. If not, the evaluation proceeds to the next step.
- Step 5: Based on the applicant's residual functional capacity (RFC), age, education, and work experience, the DDS determines if the applicant could engage in other types of employment. If so, the claim is denied. Otherwise, the claim results in a disability finding.
Motivating the sequential disability determination process is a screening strategy designed to deal first with cases that can be easily decided on the basis of fairly objective medical tests. If the claimant does not meet or equal the severity requirements in the listings of impairments, the vocational grid is used to determine whether he or she is disabled. The grid incorporates a combination of the following factors: age, RFC, education, and the skill level involved in past work as well as the degree to which those skills can be transferred to another job. Age is divided along four thresholds (younger than age 50, aged 50–54, aged 55–59, and aged 60 or older). RFC is graded into five different categories that assess the exertional limitations of the filer for work-related activities (sedentary, light, medium, heavy, and very heavy work). For the purpose of the vocational grid, SSA divides educational level into four categories (illiterate or unable to communicate in English, limited education or less, high school graduate or more, and recent education that trained the applicant for a skilled job). Assessment of previous relevant work experience leads to the categories of unskilled, semiskilled, and skilled. Finally, the determination process takes into account whether the skills the applicant learned from a past job can be transferred to a new, similar position.
Lahiri, Vaughan, and Wixon (1995) and Hu and others (2001) used household survey data matched to Social Security's administrative records to model the sequential disability determination process. Their findings indicate that the predictive ability of particular variables is linked to their relevance within the stage of determination. For instance, information on activity limitations and medical variables are significant to steps 2 and 3, while the explanatory power of age, past work, and education are manifest in steps 4 and 5.
The Appeals Process
Within 60 days from the notice of denial, the applicant has a number of sequential chances to appeal the decision. There are four stages of appeal. The first stage is a reconsideration by the state DDS, where the case is reviewed by a different examiner and the applicant has the opportunity to submit additional evidence. The second stage involves the Office of Disability Adjudication and Review (ODAR), where the claimant can request a hearing before an ALJ.2 The ALJ considers any documentary evidence introduced, evaluates the testimony of the applicant, and witnesses that testimony under oath. The third stage in the appeals process is to request a review by the Appeals Council, which is comprised of a panel of ALJs. The Council may choose to grant, deny, or dismiss the request. Upon review, the Council can uphold, reverse, or modify the decision. It can also send the case back to the ALJ for a new hearing. Finally, if the applicant is dissatisfied with the outcome, the fourth stage available is to appeal the case outside of SSA in a federal district court.
Table 1 presents allowance, denial, and appeal rates for disability determinations made at various adjudicative stages by year of application. The table reflects 100 percent of the determinations for workers applying to the DI program only, excluding concurrent applicants to DI and SSI. Results are shown for the combined 8-year period spanning the random data sample in my modeling effort (applications from 1997 through 2004), as well as separately for 2 individual years (the first (1997) and last (2004)).3 The initial disability allowance rate within the 8-year period considered stands at about 45 percent. Roughly, 63 percent of initial denials are appealed at the reconsideration stage, which results in a fairly small portion of reversals by the DDS (about 14 percent). However, 85 percent of the reconsideration denials are appealed. Once the third and fourth stages in the appeals process are reached (at the hearing level or in a federal court), denials are reversed at a rate of 78 percent. As a result, after the appeals process takes its course, the 45 percent initial disability allowance rate increases to an overall allowance rate of 70 percent.
| Count and rate of disability determination | 1997 | 2004 | 1997–2004 |
|---|---|---|---|
| Initial level | |||
| Number | |||
| Determinations | 551,909 | 736,987 | 5,151,351 |
| Allowances | 228,793 | 329,523 | 2,319,171 |
| Denials | 323,116 | 407,464 | 2,832,180 |
| Appeals | 206,148 | 248,232 | 1,778,805 |
| Percent | |||
| Allowance rate | 41.45 | 44.71 | 45.02 |
| Denial rate | 58.55 | 55.29 | 54.98 |
| Appeal rate | 63.80 | 60.92 | 62.81 |
| Reconsideration level | |||
| Number | |||
| Determinations | 206,148 | 248,232 | 1,778,805 |
| Allowances | 33,373 | 28,707 | 255,201 |
| Denials | 172,775 | 219,525 | 1,523,604 |
| Appeals | 141,021 | 185,672 | 1,288,257 |
| Percent | |||
| Allowance rate | 16.19 | 11.56 | 14.35 |
| Denial rate | 83.81 | 88.44 | 85.65 |
| Appeal rate | 81.62 | 84.58 | 84.55 |
| Hearing level or above | |||
| Number | |||
| Determinations | 141,021 | 185,672 | 1,288,257 |
| Allowances | 107,539 | 151,122 | 1,009,799 |
| Denials | 33,482 | 34,550 | 278,458 |
| Percent | |||
| Allowance rate | 76.26 | 81.39 | 78.38 |
| Denial rate | 23.74 | 18.61 | 21.62 |
| SOURCE: Author's tabulations based on the Annual Statistical Report on the Social Security Disability Insurance Program, 2008. | |||
Multiple factors can contribute to the high reversal rate of initial denials. The most obvious explanation is that many impairments can worsen over time, particularly disorders that are of a degenerative nature. One feature of the DI program is that at every stage of the appeals process the claimant has an opportunity to introduce additional medical evidence. Therefore, it is possible that ALJs are making decisions based on a more extensive information set that was simply not available to state DDS examiners. Moreover, unlike with the DDS appeals procedure, applicants at the hearing level or above are much more likely to retain legal counsel. Claimant representation benefits from detailed knowledge of the rules and process. This can be helpful in developing medical evidence that may include additional symptoms and impairments not claimed at the DDS level. In this context, the Social Security Advisory Board (2001) has made a number of recommendations addressing some of the procedural differences between the adjudicative levels (such as the fact that most claimants lack any face-to-face interaction with an adjudicator until they get to an ALJ hearing). Finally, by its very nature, the appeals process could be inducing a selection bias effect, where only the applicants with the strongest evidence appeal a denial. In fact, one possible route to selection bias is the use of legal counsel. After all, attorneys are likely to prescreen potential clients in order to represent those with the highest probability of an allowance.4
Previous Literature
SSA's statutory definition of disability in terms of "ability to work" is inevitably open to subjective judgment on the part of decision makers. In a minority of cases, proof of a specific impairment will qualify the filer for expedited case processing under the Compassionate Allowance (CAL) initiative, based on minimal, but sufficient objective medical information. Roughly, about a third of allowances are decided on the medical evidence alone (step 3), but even physicians may disagree over the interpretation of diagnostic tests. Most claimants are unlikely to neatly fit precisely defined eligibility criteria, and program guidelines can be subject to interpretation. In some instances, federal courts have issued decisions that at least for a while resulted in different disability policies for different parts of the country.5 Moreover, individuals vary in their ability to withstand pain and in their response to treatment, so that one person facing a specific set of limitations may be able to work, while another may not. Once vocational considerations such as RFC, relevant past work experience, and transferable skills are criteria in the determination process, the decision becomes increasingly complex. For these reasons alone, one would expect some degree of heterogeneity in disability outcomes.
The literature evaluating factors that affect allowance rates in Social Security's disability programs is extremely sparse. More effort has been devoted to investigating the determinants of application rates. Rupp and Stapleton (1995) summarized earlier contributions, while Rupp (2012) discussed more recent work. A growing body of evidence using different methodology and various sources of data suggests that application rates increase with labor market shocks. Higher unemployment reduces the opportunity cost of applying for marginally qualifying individuals, who must weigh their current earnings and future labor opportunities against the present value of benefits. Thus, application rates are expected to rise in response to a labor market shock. Additionally, the increase in marginally qualified applicants is anticipated to produce a decline in allowance rates, as those filers have a harder time qualifying through the determination process.
For over a decade, the Social Security Advisory Board (2001, 2006, 2012a) has been tracking the two main sources of variation in allowance rates referenced in this article (by state and adjudicative stage), calling for a major overhaul to the disability programs. Among its suggestions, the Board advocates strengthening the federal/state arrangement to decrease the large disparities that exist between different states regarding staff salaries, educational requirements, training, and attrition rates. The Board also recommends reforming the hearing process by establishing uniform procedures for claimant representatives; having the government represented at the ALJ hearing level or above; and closing the record after the ALJ decision, so that cases do not change substantially at each level of appeal.
Using a combination of aggregate time-series and cross-sectional methodology, Rupp and Stapleton (1995) found a positive relationship between the state unemployment rate and both initial applications and awards. Their modeling of allowance rates suggested the presence of lagged effects. Specifically, the authors estimated that a 1 percentage point increase in the unemployment rate was associated with a 1 percent decline in the initial allowance rate in the first and second years following the year in which the unemployment rate changed.
State allowance rates depend on the economic, demographic, and health characteristics of the applicants, which vary among the states. For instance, states with older populations are anticipated to have higher disability allowance rates on average. Older applicants are more likely to qualify because of the higher prevalence of age-related disabilities and the fact that they face less stringent program standards than do younger individuals. Using state-level data over a 3-year period (1997–1999), Strand (2002) estimated that as much as half of the variation in initial allowance rates may have been attributable to state differences in economic and demographic factors. The author found a negative association between filing rates and allowance rates and a statistically significant negative impact of unemployment on allowance rates. Institutional considerations can also play a role in explaining observed heterogeneity in disability outcomes. For instance, Coe and others (2011) found that states with mandated health insurance and longer duration for Unemployment Insurance benefits were associated with lower application rates.
In a recent article, Rupp (2012) used individual-level data over the 1993–2008 period to investigate three factors affecting initial allowance rates: (1) the demographic characteristics of applicants, (2) the diagnostic mix of applicants, and (3) local labor market conditions. The modeling approach involved a binary logit process with fixed-effects for state of origin and year of determination. Explanatory variables included the state unemployment rate and indicators for sex, age group, impairment type,6 and the presence of a secondary diagnosis code in the data. The author found these three sets of variables statistically significant. All else equal, male and older adult applicants had a higher likelihood of an initial allowance. Likewise, an increase in the state unemployment rate was associated with a decline in the probability of an initial allowance, with the size of the effect changing substantially by body system. The size of the state fixed-effects suggested that a substantial portion of the variation in state initial allowance rates could be attributed to permanent differences among the states.
Keiser (2010) explored the variation in self-reported (as opposed to actual) allowance rates among DDS examiners in three undisclosed states. The study approached the subject of outcome variation in disability decision making from the perspective of the theory of bounded rationality. The surveys mailed to DDS examiners considered a number of factors, including: (1) ideological identification; (2) adherence to conflicting goals (aiding disabled individuals, while protecting US tax payers from fraud); (3) perception about applicants' honesty in representing their limitations; and (4) the expectations of examiners' immediate supervisors (a focus on allowances, denials, or both equally). The model was able to account for only 12 percent of the variation in self-reported allowance rates. One aspect of the study relevant to the objectives here relates to the evidence of a possible policy feedback mechanism. In particular, knowledge of the extent to which ALJs reverse initial denials was found to be a factor in explaining higher reported allowance rates among examiners.
Data and Methodology
The Disability Research File (DRF) is a data file designed to longitudinally track a cohort of filers through 10 years of the disability decision and appeal process. Prompted by concern from Congress regarding the size of the disability rolls, the file—originally built in 1993—is updated once a year, with the 3 most recent years of claims data completely built from scratch. Because of differences in the structure of DI and SSI records (Title II and Title XVI, respectively, under the Social Security Act), two separate files are compiled that draw from multiple administrative data sources in a process that usually takes several months to complete. The file is unique in its ability to provide information about the status of a claim in its progression throughout the adjudicative stages, as well as activity about claimants who file multiple disability applications.
For this study, I work with a 10 percent random sample of an abbreviated version of the DRF, tracking 10 years of longitudinal disability claims (1997–2006). The analysis is restricted to medical determinations involving workers aged 18–65 who applied to the DI program during the 8-year period from 1997 through 2004. The latter is the most recent year in the file for which the percentage of pending applications is negligible. Moreover, the focus is on DI medical claims only. In particular, technical denials are excluded because they generally lack the evaluation of any medical evidence.7 Concurrent applicants to the DI and SSI programs are also excluded, as they represent a unique population that has enough work experience to qualify under DI, but that is poor enough to meet SSI's criteria. A look at the Annual Statistical Report on the Social Security Disability Insurance Program (SSA 2009, Tables 60 and 62) validates this decision. Nonconcurrent DI workers systematically experience higher allowance rates at the initial and hearing levels than concurrent workers. Furthermore, Rupp (2012, Table 1) illustrates how the age structure and diagnostic mix of both populations can differ substantially. Concurrent filers tend to be younger and have a much larger share of mental diagnoses. Thus, it seems appropriate to treat DI-only, concurrent, and SSI-only claimants as separate populations.
Formally, the adjudicative-level process can be thought of as a sequential interaction between two parties (Social Security and the applicant). Conditional on a claimant applying to the disability program, Social Security makes a decision to allow or deny. Likewise, conditional on a denial, the applicant decides whether or not to appeal. The sequence continues, with the process ending upon an allowance, a decision not to appeal, or exhaustion of all appeals opportunities. While the appeals decision is always made by the same individual (the applicant), the decision to allow or deny can be made by a field office representative, an examiner at the DDS, an ALJ, or even a federal judge. Complicating matters further is the Prototype program, which breaks the order of the sequence by allowing several states to skip the reconsideration adjudicative level.
This article focuses on the prediction of outcomes as a purely statistical classification problem. I do not model the sequential structure of the decision-making process. For purposes of this study, the disability determinations in the file are separated into four mutually exclusive categories: (1) initial allowances, (2) initial denials not appealed, (3) final allowances, and (4) final denials. This classification of the data implicitly reduces the adjudicative process to two stages. Specifically, the first two categories (initial allowances and initial denials not appealed) represent outcomes at the initial DDS level. The last two categories (final allowances and final denials) result once the applicant decides to stop appealing or exhausts the appeals process. This can occur at the reconsideration DDS level, at the hearing level, or in a federal court. In other words, what triggers the difference between the two adjudicative stages is a decision to appeal an initial denial. However, because of the low allowance rate and high appeal rate at the reconsideration stage (see Table 1), the large majority of decisions falling into the final allowance and final denial categories occur at the hearing level or above.
Table 2 breaks down the count and proportion of sample observations by adjudicative disability outcome. In the top panel of the table, out of a random sample comprising 462,578 observations, 46.2 percent of applicants receive an initial allowance, while 19.4 percent decide not to appeal an initial denial. The percentages of claimants that end up in the final allowance and final denial categories are 24.9 percent and 9.5 percent, respectively. For comparison, the bottom panel of the table displays equivalent quantities corresponding to the full data set. The outcome proportions in the 10 percent random sample suggest an adequate approximation to the population of DI claimants over the 8-year period.8
| Count and proportion | Initial | Final | Total | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| 10 percent random sample | |||||
| Number | 213,851 | 89,796 | 115,112 | 43,819 | 462,578 |
| Percent | 46.23 | 19.41 | 24.88 | 9.47 | 99.99 |
| 100 percent data file | |||||
| Number | 2,319,171 | 1,053,375 | 1,265,000 | 513,805 | 5,151,351 |
| Percent | 45.02 | 20.45 | 24.56 | 9.97 | 100.00 |
| SOURCE: Author's calculations based on a 10 percent sample of the DRF and Table 1. | |||||
| NOTE: Values may not sum to 100 because of rounding. | |||||
Summary statistics of the explanatory variables used in my modeling effort appear in Table 3. Age at filing is the only continuous predictor. As illustrated in a later section of this article, the age profiles associated with the disability outcomes are highly nonlinear. In the models, I include both age and its square as a means to capture the nonlinearity. The mean age of all filers in the sample is about 50, but on average, claimants receiving an initial allowance tend to be 2 years older, while those in the final denials category have a mean age of less than 47. All else equal, it is expected that an increase in age would be positively associated with the likelihood of an initial allowance.
| Variable | Initial | Final | Total (variable category) | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| Male | 56.29 | 49.21 | 49.20 | 48.15 | 52.38 |
| Reapplicant | 11.82 | 18.62 | 22.09 | 23.41 | 16.79 |
| Unemployed | 15.13 | 24.21 | 20.72 | 27.63 | 19.47 |
| Earnings | |||||
| Marginal | 22.47 | 36.91 | 23.63 | 37.45 | 26.98 |
| Low | 25.50 | 29.46 | 29.96 | 28.88 | 27.70 |
| Average | 26.34 | 19.63 | 25.34 | 19.59 | 24.15 |
| High | 18.44 | 10.77 | 15.88 | 10.86 | 15.60 |
| Very high | 7.25 | 3.23 | 5.19 | 3.22 | 5.58 |
| Age | |||||
| Mean | 52.15 | 47.39 | 49.58 | 46.76 | 50.08 |
| Standard deviation | 10.10 | 10.80 | 8.52 | 9.31 | 10.03 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | |||||
The models include binary indicators for sex (1 if male), for reapplication (1 if the claimant has applied to the DI program before), and for having zero earnings in the year before application (1 for zero earnings). Males comprise 52 percent of all filers in the sample, but make up 56 percent of claimants receiving an initial allowance. All else equal, it is expected that males would have a higher probability of an initial allowance. The two remaining indicator variables (reapplicants and claimants with zero earnings in the year before filing) are included because of their potential to serve as proxies for marginally qualified applicants, however imperfectly.
Following the DRF documentation, I use a 10-year window to classify an individual as having previously applied. That is, a new claimant is a person who is actually a first-time applicant or whose previous DI application dates back at least 10 years. About 17 percent of filers in the sample are reapplicants, compared with only 12 percent of those receiving an initial allowance. Notice how outcomes in the final adjudicative stages tend to have a higher share of claimants with a prior application history. Thus, it is expected that new applicants would have a higher likelihood of an initial allowance. Finally, the focus turns to a claimant's lack of earnings in the year before filing to identify those with the highest immediate financial incentive to apply. Throughout this study, such applicants are referred to as unemployed (Table 3). About 19.5 percent of claimants in the sample had zero earnings in the year before applying, compared with 24 percent and 28 percent of those in the initial denials not appealed and final denials categories, respectively. All else equal, it is anticipated that applicants with nonzero earnings in the year before filing would have a higher probability of an initial allowance.
The last explanatory variable used here is a derived field in the DRF, representing a discrete earnings index. The earnings index is constructed using the Department of Labor's official minimum wage and Social Security's Office of the Chief Actuary's national income averages. An applicant's individual earnings are compared with the minimum wage and the national income average in order to assign a numerical value (from 1–5) that indicates whether the claimant's earnings are below or above the national average. Among allowed claims, the index encompasses the 2nd through 6th years of earnings prior to the established date of disability onset. Among the denied claims, the earnings index comprises the 2nd through 6th years of earnings before the filing date. The rationale in choosing this time frame is based on a desire to avoid potential bias that is due to a sharp decline in earnings in the most recent years because of the gradual onset of disability. The earnings index categories are as follows:
- Marginal earnings.
- Low earnings—mean earnings exceed marginal earnings, up to 75 percent of the national average.
- Average earnings—mean earnings fall between 75 percent and 125 percent of the national average.
- High earnings—mean earnings fall between 125 percent and 200 percent of the national average.
- Very high earnings—mean earnings above 200 percent of the national average.
While zero earnings in the year before filing (defined here as unemployed) reflects a claimant's immediate incentive to apply, the earnings index encompasses the future earnings potential that the applicant must renounce in order to receive DI benefits. Roughly, 27 percent of filers have marginal earnings, which tend to distribute more heavily among the denial categories (36.9 percent of initial denials not appealed and 37.5 percent of final denials). That trend reverses for average, high, and very high earners. For instance, 15.6 percent of claimants in the sample are high earners. However, among applicants receiving an initial or a final allowance, their shares are 18.4 percent and 15.9 percent, respectively. Meanwhile, the proportion of high-income filers in each of the initial denials not appealed and final denials categories is less than 11 percent. All else equal, it is anticipated that higher earnings would be associated with a higher probability of an initial allowance.
The Models
The Bayesian approach to inference embodies the idea of learning from experience, through which new evidence is integrated with existing knowledge. Given observed data, a researcher (classical or Bayesian) makes probabilistic assumptions about how that data were generated (the data distribution or data model). The model contains a number of unknown parameters and the goal is typically to reach statistical conclusions about their values. Bayesian statisticians include a second element to the model (the prior distribution), which reflects prior uncertainty about the parameter values. Those two elements are combined through a mechanism known as Bayes's theorem to derive the so-called posterior distribution. The posterior probability distribution results from conditioning on the observed sample and reflects how the information in the data modifies prior knowledge. Once available, it can be used to report point estimates of the parameters, construct credible intervals and regions of the parameter space associated with some posterior probability, and estimate the posterior predictive density associated with future observations.
The prior probability distribution (often called the prior) provides a formal mechanism to explicitly incorporate available nonsample information. The prior might be specified to accommodate the empirical evidence of previous studies or for purely economic or statistical theory considerations. It may also aim at simply reflecting the views of the researcher. These are examples of informative priors. On the other hand, diffuse or noninformative priors aim at representing a lack of prior knowledge, by minimizing the influence of the prior on the resulting posterior distribution. At any rate, when a large sample of observations is involved, the data density usually dominates the prior, so that the choice of prior is inconsequential in terms of the derived posterior inference.9
The Bayesian models estimated in this analysis closely follow the description and algorithmic implementation in Rossi, Allenby and McCulloch (2005). I estimate separate hierarchical multinomial logit models that cluster the claimant-level data into states and into diagnoses. Appendix Tables A-1 and A-2 present sample counts by disability outcome for the 181 primary impairments and 50 states, respectively. Following Congdon (2005), a hierarchical multinomial logit model is often defined by the nature of the individual-level explanatory variables entertained. In this application, all of the available predictors are invariant with respect to the adjudicative disability outcome. As a result, the specification becomes a pure multinomial logit model with category-specific parameters. The parameters for a baseline outcome are typically set to zero to avoid model indeterminacy. In all cases, final denials represent the baseline. Thus, for a particular cluster (a specific state or diagnosis) and a particular outcome (an initial allowance, an initial denial not appealed, or a final allowance), there is a distinct set of parameters associated with the following explanatory variables:
- An intercept.
- A binary variable taking the value of 1 if the individual has applied to the DI program before.
- A binary variable taking the value of 1 if male.
- A discrete earnings index taking values of 1 through 5.
- A binary variable taking the value of 1 if the individual had zero earnings in the year before applying.
- The applicant's age at filing.
- The square of the applicant's age at filing.
One way to think of a hierarchical model is as a compromise between two extreme solutions. On the one hand, I could disregard the state of origin and the primary diagnosis codes and estimate a multinomial logit model that pools all the claimants together. For comparison, estimates from such a model are provided. Alternatively, I could estimate a separate model for every state and every impairment. That approach would be problematic for those groups with few observations, which is the case for many of the individual impairments. Instead, the hierarchical version of the model can be seen as a set of multinomial logit processes that are linked together through a common distributional assumption. That is, the individual parameters are assumed to derive from a multivariate normal distribution (often referred to as the heterogeneity distribution), with unknown mean and covariance matrix. Estimates of the covariance matrix can be used to decompose outcome variation into its within-group and between-group components (see for instance, Raudenbush and Bryk (2002)). Moreover, unlike the nonhierarchical version of the multinomial logit model, my approach can accommodate the possibility of correlation between the groups, although not within the groups. Finally, one virtue of hierarchical models lies in their ability to diminish the influence of outlying observations. That property (often referred to as shrinkage) is desirable in circumstances where many of the clusters contain few observations. The result is usually more reasonable parameter estimates that are not skewed by the scarcity of data or the influence of outliers in specific groups.
Once posterior estimates of the parameters are available, the models can be used to generate probability predictions.10 Given specific values of the explanatory variables, three separate equations generate linear predictions for an initial allowance, an initial denial not appealed, and a final allowance (by default, the linear prediction for a final denial takes a 0 value). These linear predictions can be transformed into probabilities using standard formulae associated with the logit model. It is important to keep in mind the distinction between a linear prediction and a probability. For a given outcome (say an initial allowance), the linear predictions allow comparison of how all the clusters (the states or diagnoses) rank within that outcome. On the other hand, the probability that the i-th applicant in the j-th group falls into say the initial allowance category is computed using the linear predictions for all four adjudicative disability outcomes combined. Thus, within a given cluster, the estimated probabilities of an initial allowance, an initial denial not appealed, a final allowance, and a final denial add to 100 percent, as they track the observed proportions in the data sample.
State Variation
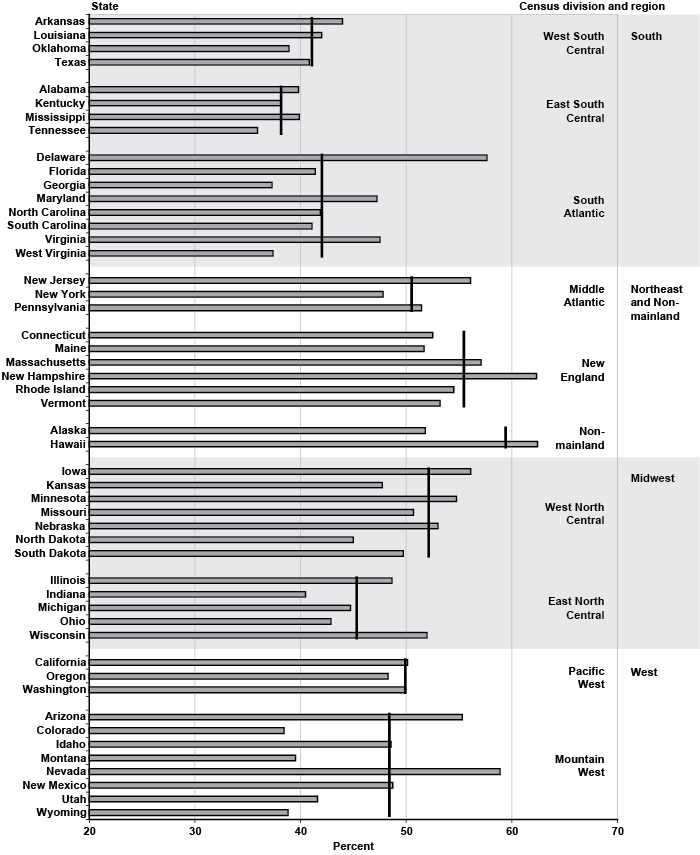
The disability outcomes in the sample for all 50 states are listed in Appendix Table A-2. In terms of sample size, California contributes 10.1 percent of total applicants, followed by New York, Florida, and Texas. These four states combined account for more than a quarter of all claimants. At the other end of the spectrum, Alaska comprises a mere 0.12 percent of the total observations (552), followed by Wyoming, North Dakota, and South Dakota. The graphs in Chart 1 display initial allowance rates by state, grouped according to the Census Bureau regions and divisions. The black vertical lines denote the overall initial allowance rate for a particular division, with the horizontal bars corresponding to each individual state. For geographical reasons, I place Alaska and Hawaii in the Nonmainland category, although technically, those two states are counted as part of the Pacific-West division.
Percentage of initial allowances, by state and Census division and region
| Location | Percent |
|---|---|
| South | |
| West South Central | 41.10 |
| Arkansas | 43.97 |
| Louisiana | 41.99 |
| Oklahoma | 38.93 |
| Texas | 40.82 |
| East South Central | 38.18 |
| Alabama | 39.83 |
| Kentucky | 38.12 |
| Mississippi | 39.87 |
| Tennessee | 35.93 |
| South Atlantic | 42.03 |
| Delaware | 57.66 |
| Florida | 41.39 |
| Georgia | 37.30 |
| Maryland | 47.24 |
| North Carolina | 41.89 |
| South Carolina | 41.07 |
| Virginia | 47.54 |
| West Virginia | 37.40 |
| Northeast and Nonmainland | |
| Middle Atlantic | 50.51 |
| New Jersey | 56.11 |
| New York | 47.81 |
| Pennsylvania | 51.47 |
| New England | 55.48 |
| Connecticut | 52.51 |
| Maine | 51.69 |
| Massachusetts | 57.09 |
| New Hampshire | 62.34 |
| Rhode Island | 54.51 |
| Vermont | 53.20 |
| Non-mainland | 59.45 |
| Alaska | 51.81 |
| Hawaii | 62.46 |
| Midwest | |
| West North Central | 52.12 |
| Iowa | 56.13 |
| Kansas | 47.74 |
| Minnesota | 54.78 |
| Missouri | 50.69 |
| Nebraska | 53.03 |
| North Dakota | 44.99 |
| South Dakota | 49.73 |
| East North Central | 45.31 |
| Illinois | 48.68 |
| Indiana | 40.49 |
| Michigan | 44.75 |
| Ohio | 42.91 |
| Wisconsin | 51.97 |
| West | |
| Pacific West | 49.93 |
| California | 50.14 |
| Oregon | 48.28 |
| Washington | 49.94 |
| Mountain West | 48.41 |
| Arizona | 55.30 |
| Colorado | 38.46 |
| Idaho | 48.57 |
| Montana | 39.54 |
| Nevada | 58.88 |
| New Mexico | 48.73 |
| Utah | 41.61 |
| Wyoming | 38.84 |
In terms of initial allowance rates, the four states with the lowest values are southern states: Tennessee (35.9 percent), Georgia (37.3 percent), West Virginia (37.4 percent), and Kentucky (38.1 percent). On the other hand, Hawaii leads with the highest initial allowance rate at 62.5 percent, followed by New Hampshire (62.3 percent), Nevada (58.9 percent), and Delaware (57.7 percent). Thus, the range of state variation in initial allowances (the difference between Hawaii with the highest initial allowance rate and Tennessee with the lowest rate) is roughly 25 percentage points. Chart 1 does not appear to reveal any clear-cut geographical patterns other than perhaps the contrast between the South and New England. Specifically, the three divisions with the lowest initial allowance rates are the southern ones (West South Central, East South Central, and South Atlantic). Clearly, Delaware and to a lesser extent Maryland and Virginia appear to be outliers in the South Atlantic division and more at home in the Middle Atlantic division. Overall, however, it is fair to say that southern states tend to have low initial allowance rates. New England, on the other hand, is the Census division with the highest allowance rate.
Diagnosis Variation
SSA maintains a classification of impairments that identify the medical conditions on which disability-related claims are based. Since 1985, the coding of primary and secondary diagnoses has approximately followed the International Classification of Diseases: 9th Revision (ICD-9) taxonomy. Appendix Table A-1 summarizes the disability outcomes for 181 medical impairments, which are grouped into 14 body systems.11 Notice that I employ the body system for descriptive purposes only, as a means of grouping individual diagnoses. To this end, each impairment is uniquely matched to a single body group, following the description in the SSA Program Data User's Manual (Panis and others 2000).
The primary diagnosis field in the data is generally based on the latest Form SSA-831 at the DDS level, but will be assigned based on an alternative source if that field is incomplete. There is evidence that on appeal, some claimants will be evaluated on the basis of a different primary diagnosis. That may occur for a number of reasons. Typically an adjudicator designates the primary impairment at the time of the decision, based on the medical evidence. However, many disability claims allege multiple impairments. Moreover, impairments may worsen and new diagnoses develop over time. As a result, additional medical evidence introduced on appeal can lead an adjudicator to change the primary impairment. Unfortunately, the DRF does not identify changes in the primary diagnosis throughout the adjudicative process. Such events are not accommodated in this analysis. An audit report from Social Security's Office of the Inspector General (SSA 2010) found that a switch in the primary diagnosis was common for three of the four impairments most likely to be denied at the initial level and allowed at the hearing level in the 2004–2006 period. These three impairments (diabetes mellitus; osteoarthrosis and allied disorders; and muscle, ligament, and fascia disorders) are prone to worsen over time and affect other body systems.12
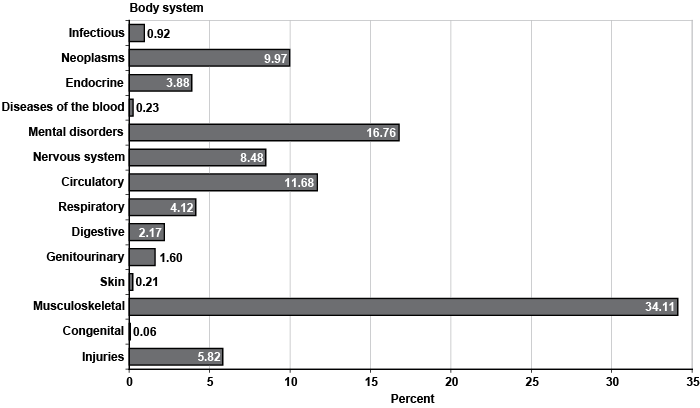
Chart 2 displays the percentage of claimants in each body system for the entire sample. Musculoskeletal impairments account for 34 percent of the diagnoses, followed by mental disorders with 17 percent. Those two body systems combined make up slightly over half of all observations. Circulatory diseases and neoplasms represent 12 percent and 10 percent of all outcomes, respectively. The nervous system and sense organs category comprises 8 percent of the impairments, while injuries make up 6 percent. Both the respiratory and the endocrine, nutritional, and metabolic body systems account for about 4 percent of claimants each. Likewise, each of the digestive and genitourinary body systems represents 2 percent of all diagnoses. Infectious and parasitic diseases contribute almost 1 percent of the observations. Finally, the remaining body groups (congenital anomalies and both diseases of the skin and subcutaneous tissue and blood and blood forming organs) represent well below 1 percent of cases combined.
Percentage of claimants, by body system
| Body system | Percent |
|---|---|
| Infectious | 0.92 |
| Neoplasms | 9.97 |
| Endocrine | 3.88 |
| Diseases of the blood | 0.23 |
| Mental disorders | 16.76 |
| Nervous system | 8.48 |
| Circulatory | 11.68 |
| Respiratory | 4.12 |
| Digestive | 2.17 |
| Genitourinary | 1.60 |
| Skin | 0.21 |
| Musculoskeletal | 34.11 |
| Congenital | 0.06 |
| Injuries | 5.82 |
A cursory look at Appendix Table A-1 reveals that one or a few primary diagnoses codes may sometimes account for the bulk of diagnoses within a body system. The tabulation below highlights selected cases. For example, disorders of the back and osteoarthrosis represent 56 percent and 21 percent of all musculoskeletal impairments, respectively, while affective and mood disorders make up more than half of the mental diagnoses. Diabetes and obesity respectively contribute 63 percent and 31 percent of claimants to the endocrine, nutritional, and metabolic body system. Four types of cancers (lung, breast, colon, and genital organs) comprise over 50 percent of the neoplasms.13 Similarly, symptomatic HIV infections are more than half of all infectious and parasitic disorders. Chronic liver disease and cirrhosis accounts for 56 percent of digestive impairments, while about 67 percent of respiratory ailments involve chronic pulmonary insufficiency. Finally, 85 percent of the genitourinary impairments are chronic renal failure, which explains the high initial allowance rate of this body system.
| Impairment | Percent |
|---|---|
| Musculoskeletal | |
| Disorders of the back—discogenic and degenerative | 55.7 |
| Osteoarthrosis and allied disorders | 20.8 |
| Mental | |
| Affective/mood disorders | 55.7 |
| Neoplastic | |
| Malignant cancers of the— | |
| Trachea, bronchus, or lung | 19.0 |
| Breast | 15.5 |
| Colon, rectum, or anus | 10.0 |
| Genital organs | 9.2 |
| Respiratory | |
| Chronic pulmonary insufficiency | 66.7 |
| Endocrine, nutritional, and metabolic | |
| Diabetes | 62.6 |
| Obesity and other hyperalimentation disorders | 30.7 |
| Digestive | |
| Chronic liver disease and cirrhosis | 55.7 |
| Genitourinary | |
| Chronic renal failure | 84.9 |
| Infectious and parasitic | |
| Symptomatic HIV infections | 52.8 |
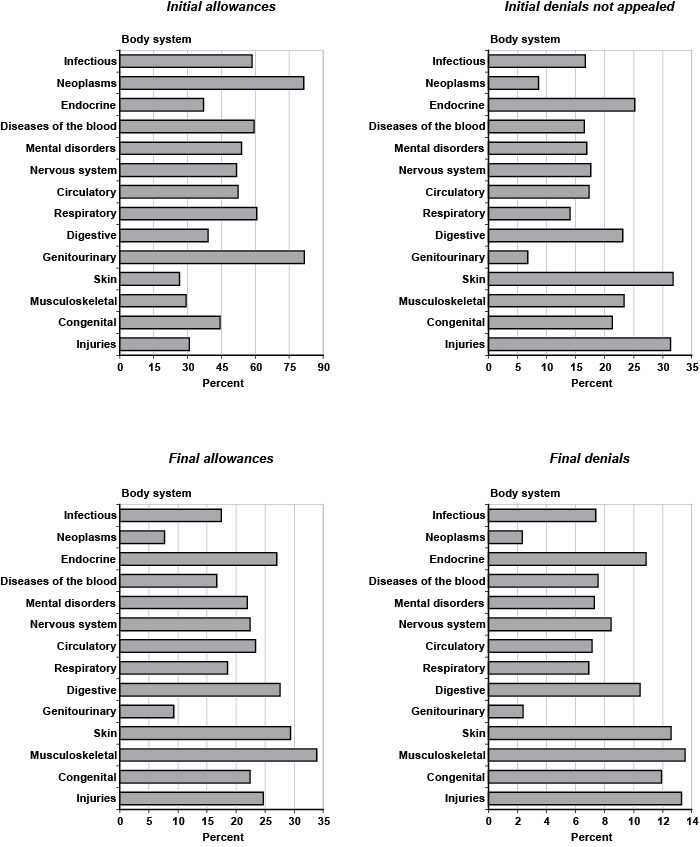
There is huge variation in disability outcomes by primary diagnosis. Chart 3 illustrates the proportion of decisions that correspond to each body system. The overall proportion of initial allowances in the sample is 46.2 percent (Table 2). However, over 80 percent of genitourinary and neoplastic impairments receive an initial allowance, while the share drops to 26.3 percent for skin disorders and to about 30 percent for musculoskeletal diagnoses. Thus, the range of variation in initial allowances among the body systems is roughly 55 percentage points. In general, the genitourinary and neoplastic body systems have the highest initial rates of allowance, exceeding any other group by at least 20 percentage points. As a result, those two groups also have the lowest proportions of initial denials not appealed, final allowances, and final denials. Applicants with injuries and skin impairments appear most likely not to appeal an initial denial, with about 31 percent of the outcomes. Musculoskeletal diagnoses have the highest proportion of final allowances, with about 34 percent of the outcomes, followed by skin disorders. In addition to injuries, however, musculoskeletal and skin impairments also exhibit the highest rates of final denials.
Percentage of adjudicative disability categories, by body system
| Body system | Initial allowances | Initial denials not appealed | Final allowances | Final denials |
|---|---|---|---|---|
| Infectious | 58.50 | 16.67 | 17.45 | 7.39 |
| Neoplasms | 81.41 | 8.61 | 7.66 | 2.32 |
| Endocrine | 36.98 | 25.18 | 26.99 | 10.85 |
| Diseases of the blood | 59.33 | 16.48 | 16.67 | 7.52 |
| Mental disorders | 53.87 | 16.92 | 21.93 | 7.28 |
| Nervous system | 51.61 | 17.57 | 22.37 | 8.45 |
| Circulatory | 52.29 | 17.28 | 23.30 | 7.13 |
| Respiratory | 60.57 | 14.02 | 18.52 | 6.89 |
| Digestive | 38.94 | 23.08 | 27.55 | 10.43 |
| Genitourinary | 81.61 | 6.75 | 9.26 | 2.38 |
| Skin | 26.29 | 31.75 | 29.38 | 12.58 |
| Musculoskeletal | 29.26 | 23.32 | 33.90 | 13.52 |
| Congenital | 44.40 | 21.30 | 22.38 | 11.91 |
| Injuries | 30.75 | 31.32 | 24.63 | 13.30 |
Mortality Variation
One source of concern regarding the categorization of outcomes in this analysis is a potential biasing effect that is due to death. Specifically, claimants with an initial denial could die before having a chance to appeal. Our DRF sample identifies an applicant's date of death over the 11-year period from 1997 through 2007. It is of course impossible to determine from the data which deaths occurred as a direct result of the underlying disability impairment. Nevertheless, this information is used to compute raw death rates (adjusted neither by age or sex) over the period in question. For the different body systems, Table 4 shows the proportion of applicants in every adjudicative outcome that passed away. About 17 percent of all claimants died during this period. However, while 28.4 percent of the applicants in the initial allowance category died, only about 7 percent of claimants who did not appeal an initial denial did not survive to 2007. Among those, two-thirds passed away at least 3 years after their application. Consequently, the potential fraction of applicants who died before having the chance to appeal would be too marginal to affect this analysis in any material way.
| Body system | Initial | Final | Total (claimant deaths in the period) | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| All | 28.37 | 6.94 | 8.75 | 5.62 | 17.17 |
| Infectious | 30.55 | 10.06 | 14.88 | 7.03 | 22.66 |
| Neoplasms | 82.27 | 21.88 | 38.78 | 16.54 | 72.21 |
| Endocrine | 23.84 | 11.82 | 14.54 | 10.48 | 16.86 |
| Diseases of the blood | 43.50 | 9.83 | 18.86 | 8.86 | 31.24 |
| Mental disorders | 8.49 | 5.41 | 6.74 | 5.25 | 7.35 |
| Nervous system | 16.03 | 5.40 | 7.59 | 5.58 | 11.39 |
| Circulatory | 25.30 | 12.49 | 14.31 | 10.05 | 19.44 |
| Respiratory | 37.83 | 11.42 | 15.08 | 9.29 | 27.95 |
| Digestive | 47.50 | 11.67 | 18.36 | 10.77 | 27.37 |
| Genitourinary | 39.20 | 9.80 | 20.26 | 10.80 | 34.79 |
| Skin | 15.69 | 5.19 | 8.42 | 4.10 | 8.76 |
| Musculoskeletal | 7.72 | 4.01 | 4.97 | 3.68 | 5.37 |
| Congenital | 18.70 | 8.47 | 9.68 | 3.03 | 12.64 |
| Injuries | 12.33 | 4.39 | 5.61 | 3.91 | 7.07 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | |||||
Deaths occurred more frequently among the most medically serious diagnoses. In terms of all outcomes, the body system with the lowest rate of mortality during the 11-year period is musculoskeletal, which is followed by injuries, mental disorders, and skin impairments. The diagnostic groups with the highest proportion of deceased claimants are neoplasms, followed by genitourinary impairments, diseases of the blood and blood forming organs, respiratory diagnoses, and digestive disorders. Given the DI program's goal to serve claimants in greater need more expeditiously, it is reassuring to see that the proportion of deceased claimants in every single body system is highest among those initially allowed and second highest for filers in the final allowance category.
It is also worth recalling that disability in the DI program is defined on the basis of long-term inability to work. As a result, death proportions and initial allowance rates are not expected to always go hand in hand. For instance, 82 percent of claimants with a neoplasm disorder who receive an initial allowance die within the 11-year period under consideration. For corresponding applicants with a genitourinary disorder (85 percent of whom have a diagnosis of chronic renal failure), mortality is lower (39 percent). Nevertheless, both body systems have similar initial allowance rates of roughly 81 percent. Standard treatments for those two impairments (such as chemotherapy and dialysis) likely pose equally severe barriers to work, even if one kind of diagnosis is much more deadly in the short run.
Age Variation
Another relevant factor of variation in disability adjudicative outcomes is age. Three important characteristics are identified in the data:
- The proportion of outcomes by single year of age is both highly nonlinear and pretty regular from one year to the next.
- There are distinct patterns at ages 50 and 55, which represent threshold points in the vocational grid.
- There is an age-62 effect that results from an influx of early retirement applicants. As pointed out by Leonesio, Vaughan, and Wixon (2003), it is a common procedure at SSA field offices to compare the potential benefits to which an applicant is entitled under more than one program. What this means in practice is that early retirees with health problems often apply concurrently for retirement and disability benefits.
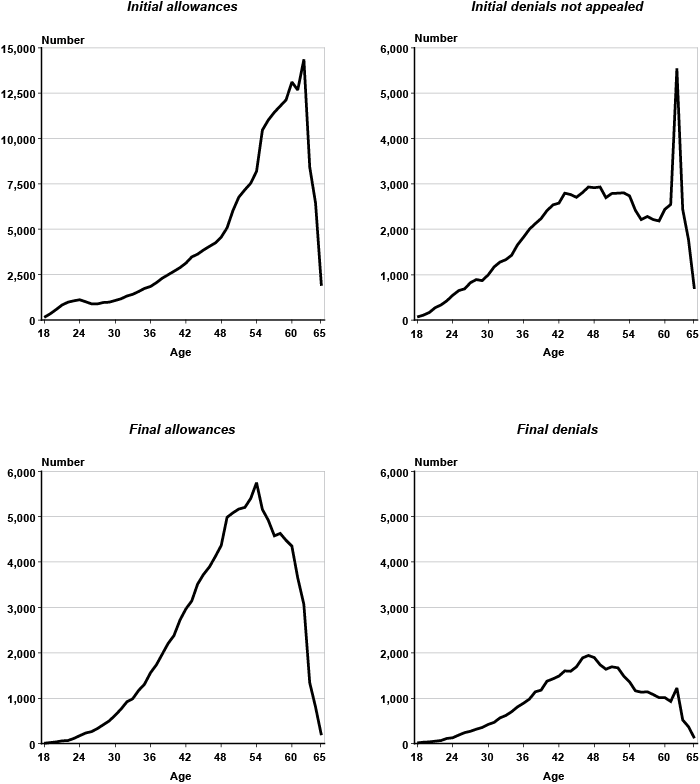
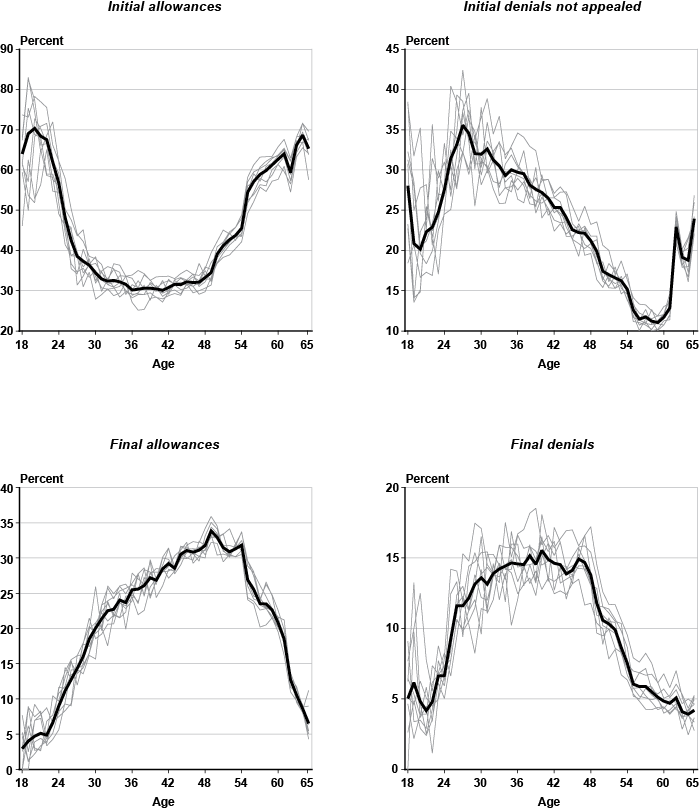
Chart 4 displays the number of claimants for each adjudicative disability outcome by single year of age (18–65). Because the focus here is on workers covered by the DI program, the total number of applicants at the youngest ages represents a tiny fraction of the sample (239 claimants at age 18 out of more than 462,000 observations). At ages 30–49, the rate at which applicants join the initial allowance category is fairly constant, but increases sharply by age 50 (top graph on the left). There are also noticeable spikes at ages 55 and 62, the latter representing a peak with over 14,000 observations. On the other hand, the number of claimants initially denied who decide not to appeal rises at a fairly constant rate up until about age 42, but levels off subsequently. The most remarkable feature in the top right graph of Chart 4 is the huge spike at age 62. The number of applicants at age 62 in this category totals more than twice that of filers at ages 61 or 63. This suggests that a substantial portion of concurrent early retirement and DI applicants receive an initial denial and decide against filing an appeal. The graph on final allowances (bottom left) shows visible spikes at ages 50 and 55, while final denials experience a jump at age 62 (bottom right).
Number of claimants, by adjudicative disability category and single year of age
| Age | Initial allowances | Initial denials not appealed | Final allowances | Final denials |
|---|---|---|---|---|
| 18 | 153 | 67 | 7 | 12 |
| 19 | 347 | 105 | 20 | 31 |
| 20 | 583 | 167 | 39 | 40 |
| 21 | 839 | 274 | 63 | 51 |
| 22 | 986 | 334 | 71 | 70 |
| 23 | 1,054 | 421 | 113 | 113 |
| 24 | 1,118 | 542 | 177 | 131 |
| 25 | 999 | 652 | 231 | 192 |
| 26 | 883 | 689 | 265 | 241 |
| 27 | 897 | 827 | 333 | 270 |
| 28 | 966 | 895 | 415 | 315 |
| 29 | 988 | 870 | 502 | 357 |
| 30 | 1,075 | 999 | 627 | 425 |
| 31 | 1,179 | 1,168 | 765 | 471 |
| 32 | 1,322 | 1,277 | 920 | 568 |
| 33 | 1,421 | 1,330 | 990 | 621 |
| 34 | 1,569 | 1,426 | 1,170 | 703 |
| 35 | 1,741 | 1,654 | 1,305 | 807 |
| 36 | 1,855 | 1,825 | 1,566 | 895 |
| 37 | 2,054 | 2,001 | 1,735 | 984 |
| 38 | 2,312 | 2,124 | 1,971 | 1,144 |
| 39 | 2,485 | 2,236 | 2,205 | 1,179 |
| 40 | 2,690 | 2,408 | 2,377 | 1,375 |
| 41 | 2,881 | 2,535 | 2,724 | 1,427 |
| 42 | 3,133 | 2,576 | 2,971 | 1,489 |
| 43 | 3,479 | 2,794 | 3,144 | 1,599 |
| 44 | 3,626 | 2,767 | 3,512 | 1,595 |
| 45 | 3,856 | 2,705 | 3,721 | 1,693 |
| 46 | 4,060 | 2,813 | 3,901 | 1,892 |
| 47 | 4,253 | 2,932 | 4,127 | 1,944 |
| 48 | 4,572 | 2,913 | 4,366 | 1,895 |
| 49 | 5,078 | 2,930 | 4,985 | 1,739 |
| 50 | 6,027 | 2,694 | 5,086 | 1,636 |
| 51 | 6,757 | 2,789 | 5,165 | 1,693 |
| 52 | 7,183 | 2,792 | 5,201 | 1,666 |
| 53 | 7,542 | 2,799 | 5,404 | 1,490 |
| 54 | 8,202 | 2,736 | 5,747 | 1,358 |
| 55 | 10,453 | 2,416 | 5,161 | 1,161 |
| 56 | 11,016 | 2,216 | 4,921 | 1,132 |
| 57 | 11,451 | 2,282 | 4,577 | 1,142 |
| 58 | 11,788 | 2,210 | 4,629 | 1,083 |
| 59 | 12,120 | 2,183 | 4,482 | 1,011 |
| 60 | 13,098 | 2,441 | 4,353 | 1,013 |
| 61 | 12,662 | 2,542 | 3,658 | 928 |
| 62 | 14,343 | 5,546 | 3,069 | 1,227 |
| 63 | 8,426 | 2,439 | 1,344 | 522 |
| 64 | 6,442 | 1,764 | 808 | 368 |
| 65 | 1,887 | 691 | 189 | 121 |
The proportion of outcomes (rates) by single year of age is shown in Chart 5. The thin discontinued lines in the chart denote the age profiles for each individual year from 1997 through 2004, while the continuous thick line corresponds to the full 8 years of data combined. The proportion of initial allowances by age displays a distinct convex "u-shape," while initial denials not appealed, final allowances, and final denials roughly follow a concave profile in the form of an "inverted-u." These patterns exhibit a great deal of regularity from one year to the next.
Percentage of adjudicative disability categories, by single year of age
| Age | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | All |
|---|---|---|---|---|---|---|---|---|---|
| Initial allowances | |||||||||
| 18 | 61.90 | 46.15 | 68.18 | 61.54 | 73.68 | 67.44 | 61.29 | 59.38 | 64.02 |
| 19 | 53.66 | 62.50 | 83.05 | 75.38 | 73.17 | 82.61 | 57.14 | 50.00 | 68.99 |
| 20 | 51.85 | 52.78 | 74.42 | 68.75 | 78.26 | 77.34 | 72.73 | 68.22 | 70.33 |
| 21 | 65.17 | 56.31 | 64.49 | 68.12 | 76.92 | 66.18 | 70.37 | 70.89 | 68.38 |
| 22 | 58.62 | 65.08 | 68.54 | 58.97 | 75.56 | 66.54 | 66.50 | 71.56 | 67.49 |
| 23 | 58.21 | 54.74 | 71.95 | 59.00 | 66.21 | 62.28 | 57.53 | 63.09 | 61.96 |
| 24 | 49.09 | 54.35 | 62.07 | 54.46 | 62.26 | 59.19 | 56.13 | 51.88 | 56.81 |
| 25 | 46.02 | 46.39 | 50.22 | 49.53 | 57.89 | 47.92 | 44.41 | 41.46 | 48.17 |
| 26 | 38.64 | 45.73 | 47.58 | 35.47 | 50.32 | 45.03 | 36.67 | 38.77 | 42.49 |
| 27 | 38.68 | 31.45 | 43.68 | 34.20 | 44.09 | 39.55 | 34.63 | 39.51 | 38.55 |
| 28 | 30.93 | 33.65 | 45.16 | 40.34 | 42.27 | 35.86 | 35.58 | 34.44 | 37.28 |
| 29 | 34.62 | 36.71 | 36.51 | 36.31 | 38.54 | 37.96 | 33.33 | 36.47 | 36.36 |
| 30 | 27.92 | 32.59 | 38.46 | 36.79 | 37.92 | 31.81 | 35.08 | 33.50 | 34.39 |
| 31 | 28.99 | 34.76 | 32.62 | 34.41 | 36.55 | 34.93 | 29.86 | 30.67 | 32.91 |
| 32 | 30.47 | 31.51 | 31.55 | 32.91 | 32.12 | 36.01 | 32.85 | 30.34 | 32.35 |
| 33 | 28.79 | 30.84 | 32.04 | 35.27 | 36.69 | 35.50 | 31.00 | 30.64 | 32.58 |
| 34 | 29.38 | 28.42 | 33.67 | 34.61 | 36.33 | 32.33 | 32.06 | 31.07 | 32.23 |
| 35 | 31.93 | 29.71 | 33.64 | 29.00 | 33.60 | 31.32 | 30.06 | 33.59 | 31.61 |
| 36 | 27.09 | 29.14 | 33.10 | 31.50 | 33.85 | 30.11 | 28.21 | 28.90 | 30.21 |
| 37 | 25.12 | 29.20 | 30.66 | 30.67 | 35.02 | 32.44 | 29.00 | 29.49 | 30.32 |
| 38 | 25.31 | 29.04 | 30.58 | 33.99 | 34.21 | 30.44 | 29.06 | 31.34 | 30.62 |
| 39 | 28.10 | 32.04 | 30.71 | 32.66 | 32.58 | 31.63 | 29.48 | 27.61 | 30.66 |
| 40 | 28.41 | 30.91 | 29.84 | 30.63 | 33.42 | 30.07 | 28.32 | 31.32 | 30.40 |
| 41 | 27.21 | 28.60 | 32.53 | 31.95 | 33.49 | 29.40 | 27.96 | 29.51 | 30.11 |
| 42 | 29.74 | 29.62 | 29.10 | 32.49 | 33.59 | 30.10 | 28.76 | 32.80 | 30.81 |
| 43 | 30.18 | 32.69 | 31.78 | 31.70 | 32.97 | 32.58 | 29.26 | 31.44 | 31.58 |
| 44 | 29.21 | 33.25 | 32.11 | 33.10 | 34.23 | 31.36 | 28.86 | 30.28 | 31.53 |
| 45 | 31.63 | 32.67 | 31.31 | 32.21 | 35.08 | 32.32 | 31.67 | 30.60 | 32.20 |
| 46 | 31.10 | 34.18 | 32.16 | 33.44 | 34.04 | 31.05 | 29.49 | 31.73 | 32.05 |
| 47 | 29.11 | 31.08 | 36.82 | 32.44 | 33.79 | 32.16 | 30.02 | 31.48 | 32.08 |
| 48 | 29.73 | 32.18 | 33.61 | 35.86 | 35.45 | 35.00 | 30.66 | 32.94 | 33.26 |
| 49 | 33.31 | 34.85 | 37.03 | 35.30 | 39.41 | 32.28 | 31.39 | 32.81 | 34.47 |
| 50 | 36.82 | 36.92 | 38.91 | 40.93 | 42.26 | 38.93 | 38.17 | 38.98 | 39.03 |
| 51 | 38.27 | 39.35 | 40.65 | 42.07 | 45.02 | 41.85 | 40.00 | 41.58 | 41.19 |
| 52 | 38.87 | 41.33 | 42.03 | 44.60 | 44.10 | 42.67 | 42.06 | 44.27 | 42.65 |
| 53 | 40.52 | 42.67 | 44.16 | 45.72 | 45.80 | 44.00 | 43.63 | 42.51 | 43.76 |
| 54 | 42.14 | 44.28 | 43.61 | 47.98 | 48.85 | 45.82 | 43.50 | 46.34 | 45.46 |
| 55 | 49.23 | 52.48 | 51.84 | 57.05 | 58.15 | 55.96 | 54.55 | 54.50 | 54.47 |
| 56 | 52.07 | 53.87 | 54.35 | 59.51 | 61.28 | 57.23 | 59.10 | 57.63 | 57.12 |
| 57 | 55.75 | 56.35 | 57.94 | 60.35 | 63.17 | 60.76 | 57.24 | 58.64 | 58.87 |
| 58 | 54.69 | 56.08 | 57.01 | 61.29 | 63.32 | 62.15 | 60.82 | 60.42 | 59.81 |
| 59 | 57.22 | 60.09 | 58.70 | 62.84 | 63.35 | 63.10 | 61.71 | 61.13 | 61.22 |
| 60 | 57.63 | 61.35 | 61.52 | 63.69 | 65.77 | 63.48 | 63.43 | 62.82 | 62.65 |
| 61 | 60.91 | 59.55 | 63.21 | 65.39 | 67.64 | 65.11 | 64.92 | 63.72 | 63.98 |
| 62 | 54.50 | 56.49 | 57.34 | 62.29 | 62.92 | 62.13 | 58.97 | 58.87 | 59.31 |
| 63 | 63.29 | 64.35 | 65.23 | 66.78 | 68.20 | 68.25 | 65.17 | 67.26 | 66.18 |
| 64 | 65.52 | 67.02 | 69.42 | 68.34 | 71.58 | 68.54 | 71.64 | 66.71 | 68.66 |
| 65 | 64.04 | 57.57 | 63.78 | 63.89 | 69.63 | 65.71 | 67.35 | 67.79 | 65.34 |
| Initial denails not appealed | |||||||||
| 18 | 38.10 | 38.46 | 22.73 | 30.77 | 18.42 | 23.26 | 32.26 | 31.25 | 28.03 |
| 19 | 31.71 | 25.00 | 13.56 | 13.85 | 20.73 | 14.13 | 28.57 | 27.94 | 20.87 |
| 20 | 35.19 | 27.78 | 15.12 | 22.32 | 16.67 | 14.84 | 20.45 | 19.63 | 20.14 |
| 21 | 22.47 | 28.16 | 25.36 | 23.91 | 17.31 | 25.49 | 21.16 | 18.35 | 22.33 |
| 22 | 35.63 | 20.63 | 21.91 | 31.41 | 16.89 | 22.43 | 23.30 | 19.91 | 22.86 |
| 23 | 26.12 | 29.93 | 17.07 | 29.00 | 22.53 | 24.20 | 27.03 | 23.61 | 24.75 |
| 24 | 33.33 | 27.17 | 25.00 | 30.99 | 24.53 | 27.41 | 26.77 | 28.20 | 27.54 |
| 25 | 26.70 | 30.41 | 32.47 | 27.57 | 25.08 | 34.82 | 31.31 | 40.42 | 31.44 |
| 26 | 31.82 | 27.64 | 27.75 | 39.32 | 30.00 | 33.92 | 34.81 | 38.41 | 33.16 |
| 27 | 37.45 | 37.10 | 32.18 | 38.53 | 32.28 | 32.03 | 42.39 | 34.35 | 35.54 |
| 28 | 39.52 | 33.65 | 30.00 | 33.45 | 29.45 | 36.65 | 36.20 | 37.46 | 34.54 |
| 29 | 30.77 | 25.52 | 34.29 | 33.43 | 32.55 | 30.10 | 34.76 | 33.82 | 32.02 |
| 30 | 30.77 | 31.01 | 29.34 | 31.35 | 28.18 | 37.76 | 30.31 | 36.55 | 31.96 |
| 31 | 35.90 | 30.48 | 32.62 | 30.25 | 29.98 | 29.60 | 33.60 | 38.88 | 32.60 |
| 32 | 31.70 | 28.54 | 30.86 | 27.64 | 32.30 | 31.19 | 32.30 | 34.46 | 31.25 |
| 33 | 33.52 | 28.29 | 30.41 | 25.85 | 26.81 | 27.83 | 33.39 | 36.66 | 30.49 |
| 34 | 27.76 | 29.81 | 28.50 | 25.87 | 27.81 | 30.74 | 31.91 | 31.39 | 29.29 |
| 35 | 27.29 | 29.56 | 29.32 | 28.70 | 27.89 | 31.87 | 32.72 | 32.98 | 30.03 |
| 36 | 30.00 | 29.28 | 26.34 | 27.50 | 28.96 | 30.37 | 30.61 | 34.60 | 29.72 |
| 37 | 32.37 | 28.93 | 25.90 | 28.52 | 28.08 | 29.57 | 29.57 | 34.05 | 29.54 |
| 38 | 28.14 | 26.44 | 28.91 | 26.88 | 25.78 | 27.71 | 28.85 | 32.92 | 28.13 |
| 39 | 25.39 | 30.32 | 24.65 | 26.15 | 25.61 | 29.04 | 27.33 | 32.41 | 27.59 |
| 40 | 29.41 | 24.04 | 26.64 | 25.86 | 27.15 | 26.85 | 28.67 | 28.80 | 27.21 |
| 41 | 26.19 | 25.22 | 25.16 | 26.49 | 24.38 | 26.54 | 28.81 | 28.84 | 26.50 |
| 42 | 24.70 | 23.77 | 22.40 | 25.37 | 25.25 | 26.55 | 27.10 | 26.56 | 25.33 |
| 43 | 25.22 | 23.45 | 23.33 | 24.30 | 24.58 | 26.03 | 27.91 | 27.24 | 25.36 |
| 44 | 22.90 | 23.55 | 22.06 | 21.73 | 23.65 | 23.55 | 26.93 | 27.29 | 24.06 |
| 45 | 21.38 | 21.37 | 22.70 | 21.79 | 21.37 | 22.62 | 23.32 | 25.52 | 22.59 |
| 46 | 23.33 | 19.25 | 22.97 | 22.42 | 20.86 | 22.34 | 22.49 | 23.65 | 22.21 |
| 47 | 21.89 | 22.83 | 19.42 | 20.72 | 20.22 | 22.54 | 23.00 | 25.48 | 22.12 |
| 48 | 21.27 | 21.18 | 19.61 | 20.26 | 20.84 | 20.93 | 21.78 | 23.22 | 21.19 |
| 49 | 19.24 | 18.34 | 16.36 | 18.50 | 18.68 | 21.32 | 21.77 | 23.55 | 19.89 |
| 50 | 17.73 | 18.58 | 15.41 | 16.68 | 16.19 | 17.46 | 16.34 | 20.62 | 17.44 |
| 51 | 16.66 | 16.11 | 17.01 | 15.34 | 15.56 | 16.44 | 18.38 | 20.00 | 17.00 |
| 52 | 15.28 | 17.94 | 16.90 | 15.30 | 16.81 | 15.88 | 17.38 | 16.97 | 16.58 |
| 53 | 16.82 | 15.32 | 14.60 | 15.73 | 15.72 | 16.26 | 16.25 | 18.72 | 16.24 |
| 54 | 14.67 | 14.51 | 15.22 | 13.81 | 13.91 | 15.17 | 17.07 | 16.36 | 15.16 |
| 55 | 13.25 | 11.66 | 12.49 | 12.41 | 11.98 | 11.18 | 13.51 | 14.11 | 12.59 |
| 56 | 12.24 | 11.41 | 11.35 | 10.72 | 10.05 | 11.06 | 11.36 | 13.33 | 11.49 |
| 57 | 11.81 | 10.90 | 10.97 | 11.12 | 11.54 | 10.72 | 12.68 | 13.25 | 11.73 |
| 58 | 11.52 | 12.66 | 10.76 | 10.02 | 11.23 | 10.22 | 10.88 | 12.49 | 11.21 |
| 59 | 11.88 | 10.91 | 11.29 | 10.21 | 10.06 | 11.24 | 10.90 | 11.83 | 11.03 |
| 60 | 13.02 | 12.01 | 12.08 | 11.24 | 10.74 | 11.98 | 10.72 | 12.03 | 11.68 |
| 61 | 13.47 | 13.99 | 12.92 | 11.40 | 11.99 | 12.51 | 11.92 | 14.63 | 12.84 |
| 62 | 24.86 | 24.24 | 24.03 | 21.83 | 21.42 | 20.95 | 23.34 | 23.18 | 22.93 |
| 63 | 20.14 | 19.80 | 18.35 | 18.21 | 19.21 | 17.91 | 20.10 | 19.50 | 19.16 |
| 64 | 21.60 | 20.29 | 16.73 | 19.14 | 16.10 | 18.00 | 17.28 | 21.38 | 18.80 |
| 65 | 23.97 | 25.99 | 22.60 | 26.85 | 22.09 | 24.21 | 22.60 | 23.78 | 23.93 |
| Final allowances | |||||||||
| 18 | 0.00 | 7.69 | 0.00 | 2.56 | 5.26 | 4.65 | 0.00 | 3.13 | 2.93 |
| 19 | 4.88 | 2.50 | 0.00 | 6.15 | 1.22 | 1.09 | 8.93 | 8.82 | 3.98 |
| 20 | 9.26 | 6.94 | 6.98 | 2.68 | 2.17 | 3.91 | 3.03 | 7.48 | 4.70 |
| 21 | 7.87 | 7.77 | 7.25 | 2.90 | 3.37 | 4.41 | 2.65 | 8.23 | 5.13 |
| 22 | 4.60 | 8.73 | 3.37 | 5.13 | 4.00 | 3.68 | 6.80 | 4.27 | 4.86 |
| 23 | 10.45 | 6.57 | 4.27 | 7.00 | 5.12 | 6.76 | 7.72 | 6.44 | 6.64 |
| 24 | 9.70 | 11.41 | 5.60 | 7.98 | 8.18 | 7.48 | 10.78 | 11.65 | 8.99 |
| 25 | 13.07 | 13.92 | 9.52 | 14.49 | 9.29 | 8.33 | 11.82 | 11.50 | 11.14 |
| 26 | 15.45 | 15.58 | 14.10 | 12.82 | 9.03 | 9.36 | 15.19 | 13.41 | 12.75 |
| 27 | 11.93 | 16.13 | 14.18 | 14.29 | 13.83 | 16.16 | 13.59 | 13.98 | 14.31 |
| 28 | 15.12 | 17.92 | 13.55 | 14.83 | 17.78 | 16.23 | 14.42 | 17.82 | 16.02 |
| 29 | 19.87 | 20.28 | 16.19 | 16.43 | 17.45 | 19.90 | 16.52 | 21.47 | 18.48 |
| 30 | 25.93 | 19.30 | 15.67 | 19.69 | 19.70 | 20.82 | 20.76 | 18.53 | 20.06 |
| 31 | 19.68 | 20.23 | 23.33 | 23.33 | 22.38 | 20.22 | 22.20 | 19.22 | 21.35 |
| 32 | 23.93 | 26.03 | 23.90 | 25.74 | 23.54 | 17.52 | 21.05 | 20.60 | 22.51 |
| 33 | 24.43 | 24.95 | 21.63 | 24.25 | 22.05 | 22.17 | 21.94 | 20.65 | 22.70 |
| 34 | 25.32 | 26.00 | 23.67 | 26.05 | 21.54 | 25.04 | 21.53 | 23.62 | 24.03 |
| 35 | 25.69 | 24.96 | 22.84 | 26.31 | 24.57 | 19.92 | 22.33 | 23.21 | 23.70 |
| 36 | 26.20 | 26.45 | 23.94 | 25.00 | 24.71 | 25.16 | 27.85 | 24.42 | 25.50 |
| 37 | 25.48 | 27.73 | 27.76 | 27.80 | 23.79 | 23.51 | 27.04 | 21.98 | 25.61 |
| 38 | 28.36 | 28.59 | 24.67 | 24.60 | 26.45 | 27.32 | 26.26 | 22.55 | 26.10 |
| 39 | 27.99 | 24.30 | 29.76 | 27.97 | 29.47 | 24.63 | 27.71 | 25.91 | 27.21 |
| 40 | 26.22 | 26.95 | 27.01 | 28.02 | 24.39 | 26.77 | 28.50 | 27.09 | 26.86 |
| 41 | 30.01 | 30.14 | 28.98 | 27.98 | 26.06 | 28.61 | 28.43 | 28.08 | 28.47 |
| 42 | 29.83 | 31.42 | 31.33 | 28.81 | 28.43 | 27.17 | 29.52 | 28.16 | 29.22 |
| 43 | 28.23 | 27.73 | 28.76 | 30.31 | 28.10 | 28.15 | 28.36 | 28.66 | 28.54 |
| 44 | 30.94 | 29.02 | 31.66 | 31.12 | 30.03 | 31.60 | 29.82 | 30.01 | 30.54 |
| 45 | 30.00 | 30.90 | 31.54 | 32.21 | 29.90 | 31.30 | 31.85 | 30.72 | 31.07 |
| 46 | 29.72 | 30.79 | 30.61 | 29.25 | 30.65 | 31.32 | 32.32 | 31.13 | 30.80 |
| 47 | 32.39 | 30.23 | 29.54 | 30.21 | 31.57 | 31.20 | 32.18 | 31.37 | 31.13 |
| 48 | 31.79 | 31.23 | 33.16 | 30.01 | 30.45 | 31.01 | 34.21 | 32.06 | 31.76 |
| 49 | 32.93 | 33.21 | 35.03 | 34.41 | 32.24 | 33.54 | 35.92 | 33.27 | 33.84 |
| 50 | 32.86 | 32.93 | 34.14 | 33.51 | 32.07 | 33.40 | 34.55 | 30.42 | 32.93 |
| 51 | 33.37 | 33.42 | 30.95 | 31.84 | 29.46 | 31.76 | 31.13 | 30.57 | 31.49 |
| 52 | 34.15 | 30.22 | 30.41 | 30.32 | 30.50 | 31.80 | 30.14 | 30.25 | 30.88 |
| 53 | 32.05 | 31.66 | 31.41 | 30.24 | 30.17 | 31.55 | 31.86 | 32.06 | 31.35 |
| 54 | 33.65 | 33.72 | 32.50 | 31.08 | 30.52 | 31.84 | 31.60 | 30.96 | 31.85 |
| 55 | 29.60 | 28.87 | 29.60 | 24.38 | 24.08 | 27.10 | 26.74 | 26.03 | 26.89 |
| 56 | 28.07 | 27.88 | 27.44 | 23.89 | 23.48 | 25.91 | 24.56 | 24.20 | 25.52 |
| 57 | 24.21 | 26.08 | 23.94 | 22.61 | 20.22 | 23.31 | 24.31 | 23.84 | 23.53 |
| 58 | 26.25 | 24.51 | 26.60 | 22.83 | 20.51 | 22.85 | 23.02 | 22.86 | 23.49 |
| 59 | 24.76 | 22.83 | 24.65 | 21.78 | 21.52 | 21.42 | 22.45 | 22.66 | 22.64 |
| 60 | 22.56 | 21.60 | 20.69 | 20.30 | 19.49 | 20.11 | 21.56 | 20.70 | 20.82 |
| 61 | 19.84 | 21.20 | 18.77 | 18.38 | 16.16 | 18.37 | 18.28 | 17.73 | 18.48 |
| 62 | 13.65 | 13.21 | 12.97 | 11.64 | 11.01 | 12.48 | 12.90 | 13.52 | 12.69 |
| 63 | 11.43 | 10.52 | 11.76 | 11.01 | 9.73 | 10.22 | 10.80 | 9.50 | 10.56 |
| 64 | 9.03 | 8.37 | 8.85 | 8.41 | 8.39 | 9.23 | 8.64 | 8.10 | 8.61 |
| 65 | 6.85 | 11.18 | 8.98 | 4.32 | 5.52 | 5.48 | 6.39 | 5.06 | 6.54 |
| Final denials | |||||||||
| 18 | 0.00 | 7.69 | 9.09 | 5.13 | 2.63 | 4.65 | 6.45 | 6.25 | 5.02 |
| 19 | 9.76 | 10.00 | 3.39 | 4.62 | 4.88 | 2.17 | 5.36 | 13.24 | 6.16 |
| 20 | 3.70 | 12.50 | 3.49 | 6.25 | 2.90 | 3.91 | 3.79 | 4.67 | 4.83 |
| 21 | 4.49 | 7.77 | 2.90 | 5.07 | 2.40 | 3.92 | 5.82 | 2.53 | 4.16 |
| 22 | 1.15 | 5.56 | 6.18 | 4.49 | 3.56 | 7.35 | 3.40 | 4.27 | 4.79 |
| 23 | 5.22 | 8.76 | 6.71 | 5.00 | 6.14 | 6.76 | 7.72 | 6.87 | 6.64 |
| 24 | 7.88 | 7.07 | 7.33 | 6.57 | 5.03 | 5.92 | 6.32 | 8.27 | 6.66 |
| 25 | 14.20 | 9.28 | 7.79 | 8.41 | 7.74 | 8.93 | 12.46 | 6.62 | 9.26 |
| 26 | 14.09 | 11.06 | 10.57 | 12.39 | 10.65 | 11.70 | 13.33 | 9.42 | 11.60 |
| 27 | 11.93 | 15.32 | 9.96 | 12.99 | 9.80 | 12.26 | 9.39 | 12.16 | 11.60 |
| 28 | 14.43 | 14.78 | 11.29 | 11.38 | 10.50 | 11.26 | 13.80 | 10.27 | 12.16 |
| 29 | 14.74 | 17.48 | 13.02 | 13.83 | 11.46 | 12.04 | 15.38 | 8.24 | 13.14 |
| 30 | 15.38 | 17.09 | 16.52 | 12.18 | 14.19 | 9.61 | 13.84 | 11.42 | 13.60 |
| 31 | 15.43 | 14.53 | 11.43 | 12.01 | 11.09 | 15.26 | 14.34 | 11.23 | 13.15 |
| 32 | 13.91 | 13.93 | 13.69 | 13.71 | 12.04 | 15.27 | 13.79 | 14.61 | 13.90 |
| 33 | 13.26 | 15.91 | 15.92 | 14.63 | 14.45 | 14.50 | 13.67 | 12.05 | 14.24 |
| 34 | 17.53 | 15.77 | 14.17 | 13.48 | 14.31 | 11.89 | 14.50 | 13.92 | 14.44 |
| 35 | 15.09 | 15.77 | 14.20 | 15.99 | 13.94 | 16.90 | 14.89 | 10.23 | 14.65 |
| 36 | 16.71 | 15.13 | 16.62 | 16.00 | 12.48 | 14.36 | 13.33 | 12.08 | 14.57 |
| 37 | 17.03 | 14.13 | 15.68 | 13.01 | 13.11 | 14.48 | 14.38 | 14.48 | 14.53 |
| 38 | 18.19 | 15.93 | 15.85 | 14.53 | 13.57 | 14.54 | 15.82 | 13.19 | 15.15 |
| 39 | 18.52 | 13.33 | 14.88 | 13.22 | 12.34 | 14.69 | 15.49 | 14.07 | 14.55 |
| 40 | 15.95 | 18.11 | 16.51 | 15.50 | 15.04 | 16.31 | 14.51 | 12.78 | 15.54 |
| 41 | 16.59 | 16.04 | 13.33 | 13.58 | 16.07 | 15.45 | 14.79 | 13.58 | 14.92 |
| 42 | 15.74 | 15.19 | 17.17 | 13.34 | 12.73 | 16.18 | 14.62 | 12.48 | 14.64 |
| 43 | 16.37 | 16.13 | 16.12 | 13.69 | 14.35 | 13.23 | 14.47 | 12.66 | 14.52 |
| 44 | 16.94 | 14.18 | 14.18 | 14.05 | 12.09 | 13.49 | 14.40 | 12.42 | 13.87 |
| 45 | 16.99 | 15.07 | 14.46 | 13.80 | 13.65 | 13.76 | 13.16 | 13.16 | 14.14 |
| 46 | 15.86 | 15.78 | 14.26 | 14.88 | 14.45 | 15.29 | 15.70 | 13.49 | 14.94 |
| 47 | 16.60 | 15.86 | 14.22 | 16.63 | 14.42 | 14.10 | 14.80 | 11.67 | 14.67 |
| 48 | 17.21 | 15.41 | 13.61 | 13.87 | 13.26 | 13.06 | 13.35 | 11.79 | 13.79 |
| 49 | 14.52 | 13.60 | 11.58 | 11.79 | 9.67 | 12.85 | 10.93 | 10.38 | 11.80 |
| 50 | 12.59 | 11.57 | 11.54 | 8.88 | 9.48 | 10.21 | 10.94 | 9.98 | 10.59 |
| 51 | 11.71 | 11.12 | 11.39 | 10.75 | 9.96 | 9.96 | 10.50 | 7.85 | 10.32 |
| 52 | 11.70 | 10.50 | 10.65 | 9.78 | 8.59 | 9.65 | 10.42 | 8.51 | 9.89 |
| 53 | 10.60 | 10.35 | 9.82 | 8.30 | 8.30 | 8.19 | 8.26 | 6.71 | 8.65 |
| 54 | 9.54 | 7.49 | 8.67 | 7.13 | 6.71 | 7.16 | 7.83 | 6.35 | 7.53 |
| 55 | 7.92 | 6.99 | 6.07 | 6.16 | 5.78 | 5.76 | 5.20 | 5.36 | 6.05 |
| 56 | 7.62 | 6.85 | 6.86 | 5.88 | 5.19 | 5.80 | 4.99 | 4.84 | 5.87 |
| 57 | 8.23 | 6.67 | 7.15 | 5.92 | 5.08 | 5.22 | 5.76 | 4.27 | 5.87 |
| 58 | 7.54 | 6.76 | 5.64 | 5.85 | 4.94 | 4.78 | 5.27 | 4.24 | 5.49 |
| 59 | 6.13 | 6.18 | 5.36 | 5.17 | 5.07 | 4.23 | 4.95 | 4.38 | 5.11 |
| 60 | 6.79 | 5.04 | 5.71 | 4.78 | 4.00 | 4.43 | 4.29 | 4.45 | 4.85 |
| 61 | 5.79 | 5.25 | 5.10 | 4.82 | 4.21 | 4.01 | 4.88 | 3.92 | 4.69 |
| 62 | 7.00 | 6.06 | 5.66 | 4.24 | 4.66 | 4.44 | 4.78 | 4.43 | 5.07 |
| 63 | 5.14 | 5.33 | 4.66 | 4.00 | 2.86 | 3.62 | 3.93 | 3.74 | 4.10 |
| 64 | 3.84 | 4.33 | 5.00 | 4.11 | 3.94 | 4.23 | 2.45 | 3.81 | 3.92 |
| 65 | 5.14 | 5.26 | 4.64 | 4.94 | 2.76 | 4.61 | 3.65 | 3.37 | 4.19 |
For the youngest claimants, the initial allowance rate is very high, ranging from 60 to 70 percent at ages 18–23 (top graph on the left). Then, the rate declines rapidly, reaching 34 percent by age 30, where it remains stable in the low-to-mid 30 percent range until age 49. The subsequent increase resembles a piece-wise linear function with discontinuities at ages 50 and 55 and a dip at the early retirement age. The rate of initial denials not appealed (top graph on the right) rises from about 20 percent at age 20 to its peak of 35.5 percent by age 27. It steadily declines from this point forward, reaching its lowest value of 11 percent at age 59. As retirement nears, the rate increases again, with the early retiree effect inducing a sizeable jump at age 62. The final allowance rate (bottom graph on the left) rises steadily to its peak of 34 percent at age 50, declining rapidly afterwards. Finally, the rate of final denials (bottom graph on the right) hovers below 15 percent at ages 32–48, declining to about 5 percent by age 55.
One interesting aspect of the age profiles is their nonlinearity. Specifically, the convex shape in the proportion of initial allowances might appear at odds with the notion that age is a reasonable proxy for health. Beyond some threshold age range, it is reasonable to expect the initial allowance rate to rise. After all, the increasing prevalence of serious age-related disabilities and less stringent vocational standards of the program are bound to push allowance rates upward. But what explains the high initial allowance rates for claimants at a very young age? One plausible answer is that the high allowance rates are driven by the impairment severity of a tiny number of applicants from an otherwise very healthy pool of workers. In addition, the contributory requirements of the DI program could be creating a bottleneck effect, with young disabled workers waiting to reach insured status. A look at the diagnostic makeup of claimants by age reveals some insights.
Chart 6 displays the distribution of claimants for the most common body systems by single year of age. About 60 percent of the small fraction of applicants aged 18–23 receive a mental diagnosis. Because mental impairments tend to have a very early onset, they indeed dominate the composition of claimants until about age 30. From age 31 forward, musculoskeletal impairments become the most common diagnosis. On the other hand, the share of mental impairments declines steadily with age. By ages 55 and 57, circulatory disorders and neoplasms surpass mental impairments to respectively become the second and third leading groups of diagnoses.
Percentage of claimants, by selected body systems and single year of age
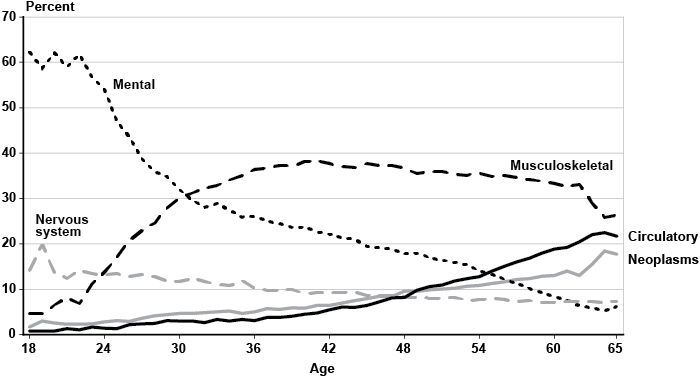
| Age | Neoplasms | Mental disorders | Nervous system and sense organs | Circulatory | Musculoskeletal |
|---|---|---|---|---|---|
| 18 | 1.67 | 62.34 | 14.23 | 0.84 | 4.60 |
| 19 | 2.98 | 58.65 | 19.88 | 0.80 | 4.57 |
| 20 | 2.53 | 62.00 | 13.51 | 0.84 | 6.51 |
| 21 | 2.28 | 58.92 | 12.39 | 1.30 | 8.23 |
| 22 | 2.33 | 61.81 | 14.17 | 1.03 | 6.84 |
| 23 | 2.41 | 56.79 | 13.46 | 1.70 | 11.23 |
| 24 | 2.79 | 54.01 | 13.11 | 1.42 | 13.72 |
| 25 | 3.09 | 46.91 | 13.40 | 1.35 | 17.07 |
| 26 | 2.89 | 43.60 | 12.80 | 2.21 | 20.84 |
| 27 | 3.61 | 38.68 | 13.32 | 2.41 | 22.95 |
| 28 | 4.17 | 35.93 | 12.77 | 2.51 | 24.66 |
| 29 | 4.42 | 34.82 | 11.70 | 3.13 | 27.82 |
| 30 | 4.64 | 31.96 | 11.74 | 3.04 | 30.04 |
| 31 | 4.69 | 29.64 | 12.39 | 2.99 | 31.17 |
| 32 | 4.82 | 28.14 | 11.74 | 2.69 | 32.18 |
| 33 | 5.02 | 28.89 | 11.00 | 3.35 | 32.83 |
| 34 | 5.16 | 27.44 | 10.78 | 3.02 | 34.02 |
| 35 | 4.68 | 25.89 | 11.86 | 3.32 | 35.10 |
| 36 | 5.03 | 26.01 | 10.10 | 3.13 | 36.43 |
| 37 | 5.76 | 25.10 | 9.83 | 3.82 | 36.77 |
| 38 | 5.52 | 24.43 | 9.83 | 3.76 | 37.27 |
| 39 | 5.93 | 23.73 | 9.93 | 4.06 | 37.19 |
| 40 | 5.86 | 23.75 | 9.10 | 4.47 | 38.11 |
| 41 | 6.43 | 22.63 | 9.29 | 4.80 | 38.24 |
| 42 | 6.46 | 22.10 | 9.27 | 5.45 | 37.62 |
| 43 | 7.00 | 21.45 | 9.22 | 6.10 | 36.98 |
| 44 | 7.52 | 20.96 | 9.45 | 6.03 | 36.77 |
| 45 | 7.90 | 19.50 | 8.72 | 6.44 | 37.76 |
| 46 | 8.50 | 19.18 | 8.74 | 7.25 | 37.16 |
| 47 | 8.41 | 18.89 | 8.53 | 8.08 | 37.18 |
| 48 | 9.57 | 17.77 | 8.32 | 8.16 | 36.61 |
| 49 | 9.52 | 17.99 | 8.31 | 9.76 | 35.62 |
| 50 | 9.86 | 16.93 | 8.03 | 10.55 | 35.93 |
| 51 | 10.05 | 16.40 | 8.02 | 10.96 | 35.89 |
| 52 | 10.21 | 15.91 | 8.31 | 11.80 | 35.42 |
| 53 | 10.65 | 15.33 | 7.61 | 12.35 | 35.16 |
| 54 | 10.88 | 14.12 | 7.68 | 12.80 | 35.55 |
| 55 | 11.31 | 13.24 | 7.90 | 14.05 | 34.92 |
| 56 | 11.65 | 12.18 | 7.65 | 15.07 | 35.04 |
| 57 | 12.19 | 11.25 | 7.29 | 16.08 | 34.55 |
| 58 | 12.34 | 10.23 | 7.48 | 16.84 | 34.21 |
| 59 | 12.91 | 9.27 | 7.07 | 18.02 | 33.75 |
| 60 | 13.09 | 8.32 | 7.18 | 18.86 | 33.28 |
| 61 | 13.98 | 7.59 | 7.21 | 19.21 | 32.50 |
| 62 | 13.04 | 6.38 | 7.41 | 20.49 | 33.11 |
| 63 | 15.55 | 5.92 | 7.20 | 22.02 | 29.08 |
| 64 | 18.44 | 5.27 | 7.07 | 22.49 | 25.79 |
| 65 | 17.69 | 6.27 | 7.44 | 21.64 | 26.32 |
Inferential Results
For each hierarchical structure (claimants nested by state or diagnosis), two model specifications are contemplated. Each model is estimated initially with no explanatory variables other than intercepts. The intercepts-only specification is useful to apportion unconditional data variance between hierarchical levels. It also provides a benchmark lower bound to goodness-of-fit criteria, which can be used for comparison purposes. The second specification entertains the previously described individual-level predictors. In addition, estimates are provided for a pooled or nonhierarchical model that does not entertain any grouping of the data.
Next, I consider two different metrics for goodness-of-fit assessment. One measure that is particularly convenient in the context of Bayesian hierarchical models is the deviance information criterion (DIC), proposed by Spiegelhalter and others (2002). The DIC can be seen as the Bayesian analogous to the classical Akaike information criterion. It incorporates cross-validation and penalizes excess complexity. When comparing multiple specifications, the smaller the DIC value, the better the model's fit. DIC estimates are presented in the following tabulation. Additionally, I compute the percentage of observations correctly predicted by each model, shown in Table 5. In this case, an observed outcome is treated as a correct prediction if its estimated posterior mean probability is higher than the mean classification probabilities of the three other remaining outcomes.
| Model specification | DIC estimate |
|---|---|
| Intercepts only | |
| Pooled | 1,151,155.30 |
| State | 1,140,108.40 |
| Diagnosis | 1,038,875.60 |
| Individual-level inputs | |
| Pooled | 1,093,989.10 |
| State | 1,080,995.40 |
| Diagnosis | 980,212.70 |
| Model | Initial | Final | Total (correctly categorized) | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| Intercepts only | |||||
| Pooled | 100.00 | 0 | 0 | 0 | 46.23 |
| State | 97.18 | 0 | 5.38 | 0 | 46.26 |
| Diagnosis | 83.68 | 18.06 | 37.18 | 0 | 51.45 |
| Individual-level inputs | |||||
| Pooled | 90.80 | 6.35 | 17.07 | 0 | 47.46 |
| State | 85.89 | 9.43 | 27.95 | 0.03 | 48.50 |
| Diagnosis | 87.84 | 24.80 | 39.50 | 0.20 | 55.27 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | |||||
Both measures of model fit provide a consistent picture. First, for a given set of variables, there is an unequivocal advantage in grouping claimants by state rather than pooling them together and in grouping them by impairment rather than clustering them by state. Consider for instance the top entry in Table 5, which corresponds to the intercepts-only pooled multinomial logit specification. As there are no explanatory variables, the estimated probability of any observation within a category is simply the sample proportion. All claimants are predicted to receive an initial allowance because this is the outcome that occurs most often. As a result, all of the initial allowances, but none of the other outcomes, are correctly categorized. This provides a lower predictive bound of 46.23 percent of the decisions correctly classified.
One way to think of a model with only intercepts is as a naive classification rule. In a hierarchical context, all individual outcomes within say a state or a diagnosis are predicted to be equal to the disability category with the highest sample proportion for that state or diagnosis. In grouping claimants by state, the intercepts-only model variant achieves some very modest gains relative to the pooled specification (46.26 percent). On the other hand, prediction improves more significantly if claimants are clustered by diagnosis (51.45 percent). When claimant-level explanatory variables are accommodated, the hierarchical diagnosis model can accurately classify 55.27 percent of the observations. The DIC estimates result in a similar ranking of the models.
A second conclusion can be drawn from Table 5. Notice how the diagnosis model with only intercepts correctly predicts a larger share of observations (51.45 percent) than the state model with claimant-level explanatory variables (48.50 percent). The same conclusion is reached when comparing the DIC estimates in the tabulation on the previous page (1,038,875 versus 1,080,995). This suggests that the primary diagnosis codes carry greater predictive ability than all other explanatory variables that are entertained combined. To put it differently, grouping a sample of claimants by diagnosis alone (the naive classification rule implied by an intercept-only model) will predict the adjudicative disability decision outcomes more accurately than knowing everything else, including age, sex, state of origin, application history, earnings history, and employment status in the year before filing. This finding is hardly unexpected, considering the role medical impairments play in the disability determination process. However, the result suggests that the full range of primary diagnosis codes (which are often overlooked for the purpose of research) is a crucial piece of information among the limited set of useful variables typically available from administrative data extracts.
Average Effects
The top portion of Table 6 presents posterior means and standard deviations of the regression coefficients in the pooled multinomial logit model.14 The bottom part of the table displays estimates corresponding to the so-called average effects of the hierarchical diagnosis model. These parameters represent the mean of the distribution of the diagnosis-specific coefficients (that is, the estimated means of the multivariate normal heterogeneity distribution). For both models (pooled and hierarchical), the estimates tend to have similar signs and magnitudes, although as expected, the standard deviations are much higher in the hierarchical version of the process.
| Variable | Initial allowances | Initial denials not appealed | Final allowances | |||
|---|---|---|---|---|---|---|
| Mean | Standard deviation | Mean | Standard deviation | Mean | Standard deviation | |
| Pooled multinomial logit | ||||||
| Intercept | 1.252581 | 0.007014 | 0.568303 | 0.007492 | 1.060417 | 0.007195 |
| Reapplicant | -0.427993 | 0.013526 | -0.207347 | 0.014696 | 0.143670 | 0.013884 |
| Male | 0.121928 | 0.011101 | 0.026245 | 0.012352 | -0.086577 | 0.011496 |
| Earnings | 0.236173 | 0.005119 | -0.013485 | 0.005773 | 0.215522 | 0.005406 |
| Unemployed | -0.614464 | 0.013845 | -0.159045 | 0.013977 | -0.292570 | 0.013669 |
| Age | 0.085465 | 0.000775 | 0.031423 | 0.000837 | 0.031753 | 0.000817 |
| Age2 | 0.004253 | 0.000051 | 0.002366 | 0.000055 | -0.000036 | 0.000058 |
| Hierarchical diagnosis multinomial logit (average effects) | ||||||
| Intercept | 1.682253 | 0.131225 | 0.698521 | 0.046508 | 1.213439 | 0.057412 |
| Reapplicant | -0.363732 | 0.060715 | -0.198089 | 0.061695 | 0.202028 | 0.061481 |
| Male | 0.200885 | 0.054438 | 0.107004 | 0.052963 | -0.069526 | 0.054504 |
| Earnings | 0.242488 | 0.040234 | -0.029794 | 0.039516 | 0.220765 | 0.041297 |
| Unemployed | -0.655286 | 0.064591 | -0.213411 | 0.062811 | -0.332018 | 0.064286 |
| Age | 0.081470 | 0.030319 | 0.027600 | 0.030594 | 0.016404 | 0.029204 |
| Age2 | 0.011028 | 0.027359 | 0.001629 | 0.027164 | 0.002343 | 0.027872 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | ||||||
Given a particular observation and model, three equations yield continuous linear predictions of an initial allowance, an initial denial not appealed, and a final allowance. Those linear predictions are defined in reference to the benchmark category of final denials, which has a zero linear prediction by design. All else equal and relative to an initial denial, the sign of the estimated coefficients implies the following effects at the claimant level:
- The linear prediction of an initial allowance: (1) increases for males and higher earners, and (2) decreases for unemployed applicants and claimants who have applied before.
- The linear prediction of an initial denial not appealed: (1) increases for males; and (2) decreases for higher earners, unemployed applicants, and claimants who have applied before.
- The linear prediction of a final allowance: (1) increases for higher earners and claimants who have applied before, and (2) decreases for males and unemployed applicants.
At the individual level, the estimated effects for the explanatory variables match my a priori expectations. The results also appear consistent with research by Rupp (2012), who also used claimant-level data. Specifically, Rupp's "fixed-effects" binary logit model for initial determinations yielded qualitatively similar conclusions about the impact of sex and unemployment on the initial allowance rate. Of course, there are substantial differences in the two modeling approaches. Rupp (2012) used the time-varying state unemployment rates, while I do not control for year-effects and instead define unemployment at the individual level (as having zero earnings in the year prior to application). All else equal, the higher the earnings category, the higher the opportunity cost of filing for DI benefits, which may explain the positive association I find between earnings and the predictions of both an initial and a final allowance. Meanwhile, a history of previous applications shows a negative impact on the likelihood of an initial allowance, but a positive impact on the likelihood of a final allowance. In addition, I find that reapplicants are more likely to appeal an initial denial.
The interpretation of the parameters associated with age is less tractable because of the fact that those parameters represent the coefficients of a quadratic polynomial. Aggregate point and interval probability predictions for each outcome by single year of age are presented in Chart 7. Those predictions are obtained by averaging over the estimated probabilities of all the claimants in the sample who are the same age. The shaded areas in the graphs represent 90 percent posterior credible intervals (in other words, intervals containing 90 percent posterior probability). The thin dark lines along the intervals correspond to the posterior mean of each prediction. In addition, the solid dots show the actual proportions observed in the sample.
Aggregate point and interval probability predictions for each adjudicative disability category, by single year of age
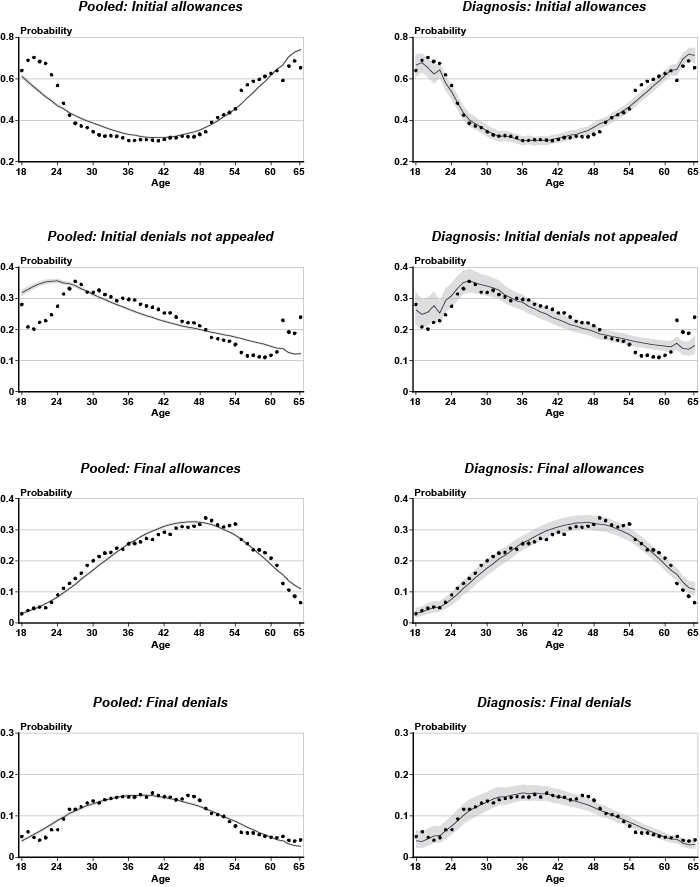
| Age | Actual | 5th percentile | 50th percentile | 95th percentile |
|---|---|---|---|---|
| Pooled: Initial allowances | ||||
| 18 | 64.02 | 60.23 | 61.10 | 61.97 |
| 19 | 68.99 | 57.85 | 58.67 | 59.48 |
| 20 | 70.33 | 55.38 | 56.14 | 56.91 |
| 21 | 68.38 | 53.00 | 53.71 | 54.43 |
| 22 | 67.49 | 50.69 | 51.36 | 52.03 |
| 23 | 61.96 | 48.69 | 49.31 | 49.93 |
| 24 | 56.81 | 46.45 | 47.03 | 47.61 |
| 25 | 48.17 | 45.11 | 45.65 | 46.18 |
| 26 | 42.49 | 43.14 | 43.64 | 44.14 |
| 27 | 38.55 | 41.76 | 42.22 | 42.68 |
| 28 | 37.28 | 40.47 | 40.90 | 41.33 |
| 29 | 36.36 | 39.31 | 39.71 | 40.12 |
| 30 | 34.39 | 38.29 | 38.67 | 39.05 |
| 31 | 32.91 | 37.25 | 37.61 | 37.97 |
| 32 | 32.35 | 36.14 | 36.48 | 36.82 |
| 33 | 32.58 | 35.22 | 35.55 | 35.87 |
| 34 | 32.23 | 34.29 | 34.60 | 34.91 |
| 35 | 31.61 | 33.53 | 33.83 | 34.13 |
| 36 | 30.21 | 32.82 | 33.11 | 33.40 |
| 37 | 30.32 | 32.53 | 32.82 | 33.10 |
| 38 | 30.62 | 31.91 | 32.19 | 32.47 |
| 39 | 30.66 | 31.55 | 31.83 | 32.10 |
| 40 | 30.40 | 31.34 | 31.61 | 31.88 |
| 41 | 30.11 | 31.46 | 31.73 | 32.00 |
| 42 | 30.81 | 31.46 | 31.73 | 31.99 |
| 43 | 31.58 | 31.78 | 32.05 | 32.32 |
| 44 | 31.53 | 32.14 | 32.41 | 32.68 |
| 45 | 32.20 | 32.72 | 32.99 | 33.26 |
| 46 | 32.05 | 33.38 | 33.65 | 33.92 |
| 47 | 32.08 | 34.02 | 34.29 | 34.57 |
| 48 | 33.26 | 35.08 | 35.36 | 35.63 |
| 49 | 34.47 | 36.35 | 36.63 | 36.90 |
| 50 | 39.03 | 37.75 | 38.03 | 38.30 |
| 51 | 41.19 | 39.43 | 39.71 | 39.99 |
| 52 | 42.65 | 41.39 | 41.67 | 41.94 |
| 53 | 43.76 | 43.24 | 43.52 | 43.79 |
| 54 | 45.46 | 45.31 | 45.59 | 45.87 |
| 55 | 54.47 | 47.74 | 48.02 | 48.30 |
| 56 | 57.12 | 50.50 | 50.78 | 51.05 |
| 57 | 58.87 | 53.07 | 53.35 | 53.63 |
| 58 | 59.81 | 55.88 | 56.16 | 56.45 |
| 59 | 61.22 | 58.56 | 58.85 | 59.14 |
| 60 | 62.65 | 61.52 | 61.81 | 62.10 |
| 61 | 63.98 | 64.43 | 64.73 | 65.02 |
| 62 | 59.31 | 66.30 | 66.62 | 66.93 |
| 63 | 66.18 | 70.36 | 70.66 | 70.96 |
| 64 | 68.66 | 72.68 | 72.99 | 73.30 |
| 65 | 65.34 | 73.74 | 74.08 | 74.42 |
| Pooled: Initial denials not appealed | ||||
| 18 | 28.03 | 31.03 | 31.87 | 32.72 |
| 19 | 20.87 | 32.13 | 32.93 | 33.73 |
| 20 | 20.14 | 33.17 | 33.93 | 34.69 |
| 21 | 22.33 | 34.06 | 34.76 | 35.47 |
| 22 | 22.86 | 34.66 | 35.32 | 35.97 |
| 23 | 24.75 | 34.91 | 35.53 | 36.14 |
| 24 | 27.54 | 35.10 | 35.68 | 36.25 |
| 25 | 31.44 | 34.50 | 35.04 | 35.57 |
| 26 | 33.16 | 34.28 | 34.79 | 35.28 |
| 27 | 35.54 | 33.60 | 34.07 | 34.54 |
| 28 | 34.54 | 32.70 | 33.13 | 33.57 |
| 29 | 32.02 | 31.87 | 32.28 | 32.69 |
| 30 | 31.96 | 30.94 | 31.33 | 31.71 |
| 31 | 32.60 | 30.10 | 30.47 | 30.83 |
| 32 | 31.25 | 29.29 | 29.64 | 29.99 |
| 33 | 30.49 | 28.48 | 28.82 | 29.15 |
| 34 | 29.29 | 27.73 | 28.05 | 28.36 |
| 35 | 30.03 | 26.98 | 27.29 | 27.60 |
| 36 | 29.72 | 26.20 | 26.50 | 26.80 |
| 37 | 29.54 | 25.47 | 25.76 | 26.06 |
| 38 | 28.13 | 24.80 | 25.09 | 25.38 |
| 39 | 27.59 | 24.19 | 24.47 | 24.75 |
| 40 | 27.21 | 23.62 | 23.90 | 24.17 |
| 41 | 26.50 | 22.95 | 23.22 | 23.49 |
| 42 | 25.33 | 22.41 | 22.68 | 22.95 |
| 43 | 25.36 | 21.88 | 22.15 | 22.41 |
| 44 | 24.06 | 21.38 | 21.64 | 21.90 |
| 45 | 22.59 | 20.89 | 21.14 | 21.39 |
| 46 | 22.21 | 20.49 | 20.73 | 20.98 |
| 47 | 22.12 | 20.14 | 20.39 | 20.63 |
| 48 | 21.19 | 19.73 | 19.97 | 20.20 |
| 49 | 19.89 | 19.29 | 19.53 | 19.76 |
| 50 | 17.44 | 18.92 | 19.15 | 19.37 |
| 51 | 17.00 | 18.51 | 18.73 | 18.95 |
| 52 | 16.58 | 18.11 | 18.32 | 18.54 |
| 53 | 16.24 | 17.79 | 18.00 | 18.20 |
| 54 | 15.16 | 17.37 | 17.58 | 17.78 |
| 55 | 12.59 | 16.87 | 17.07 | 17.27 |
| 56 | 11.49 | 16.38 | 16.57 | 16.77 |
| 57 | 11.73 | 15.94 | 16.14 | 16.33 |
| 58 | 11.21 | 15.43 | 15.62 | 15.82 |
| 59 | 11.03 | 14.97 | 15.17 | 15.36 |
| 60 | 11.68 | 14.39 | 14.58 | 14.78 |
| 61 | 12.84 | 13.79 | 13.99 | 14.19 |
| 62 | 22.93 | 13.71 | 13.92 | 14.14 |
| 63 | 19.16 | 12.35 | 12.56 | 12.76 |
| 64 | 18.80 | 11.87 | 12.08 | 12.30 |
| 65 | 23.93 | 12.00 | 12.24 | 12.48 |
| Pooled: Final allowances | ||||
| 18 | 2.93 | 2.86 | 3.01 | 3.17 |
| 19 | 3.98 | 3.53 | 3.69 | 3.87 |
| 20 | 4.70 | 4.26 | 4.44 | 4.64 |
| 21 | 5.13 | 5.03 | 5.23 | 5.44 |
| 22 | 4.86 | 5.96 | 6.18 | 6.41 |
| 23 | 6.64 | 6.95 | 7.19 | 7.43 |
| 24 | 8.99 | 8.13 | 8.38 | 8.64 |
| 25 | 11.14 | 9.41 | 9.68 | 9.96 |
| 26 | 12.75 | 10.75 | 11.03 | 11.32 |
| 27 | 14.31 | 12.18 | 12.47 | 12.77 |
| 28 | 16.02 | 13.79 | 14.09 | 14.40 |
| 29 | 18.48 | 15.23 | 15.54 | 15.85 |
| 30 | 20.06 | 16.75 | 17.05 | 17.37 |
| 31 | 21.35 | 18.21 | 18.51 | 18.82 |
| 32 | 22.51 | 19.72 | 20.03 | 20.33 |
| 33 | 22.70 | 21.14 | 21.44 | 21.74 |
| 34 | 24.03 | 22.56 | 22.86 | 23.15 |
| 35 | 23.70 | 23.84 | 24.13 | 24.43 |
| 36 | 25.50 | 25.22 | 25.51 | 25.80 |
| 37 | 25.61 | 26.24 | 26.53 | 26.82 |
| 38 | 26.10 | 27.43 | 27.73 | 28.02 |
| 39 | 27.21 | 28.44 | 28.73 | 29.03 |
| 40 | 26.86 | 29.29 | 29.58 | 29.88 |
| 41 | 28.47 | 30.07 | 30.37 | 30.66 |
| 42 | 29.22 | 30.80 | 31.10 | 31.39 |
| 43 | 28.54 | 31.31 | 31.61 | 31.90 |
| 44 | 30.54 | 31.77 | 32.07 | 32.36 |
| 45 | 31.07 | 32.08 | 32.37 | 32.67 |
| 46 | 30.80 | 32.20 | 32.50 | 32.79 |
| 47 | 31.13 | 32.27 | 32.57 | 32.86 |
| 48 | 31.76 | 32.14 | 32.43 | 32.73 |
| 49 | 33.84 | 31.86 | 32.16 | 32.45 |
| 50 | 32.93 | 31.41 | 31.69 | 31.98 |
| 51 | 31.49 | 30.77 | 31.05 | 31.33 |
| 52 | 30.88 | 29.87 | 30.14 | 30.42 |
| 53 | 31.35 | 28.95 | 29.21 | 29.48 |
| 54 | 31.85 | 27.92 | 28.18 | 28.44 |
| 55 | 26.89 | 26.68 | 26.94 | 27.19 |
| 56 | 25.52 | 25.14 | 25.39 | 25.63 |
| 57 | 23.53 | 23.63 | 23.87 | 24.11 |
| 58 | 23.49 | 21.98 | 22.21 | 22.45 |
| 59 | 22.64 | 20.32 | 20.55 | 20.79 |
| 60 | 20.82 | 18.55 | 18.78 | 19.01 |
| 61 | 18.48 | 16.79 | 17.01 | 17.23 |
| 62 | 12.69 | 15.28 | 15.50 | 15.72 |
| 63 | 10.56 | 13.35 | 13.56 | 13.77 |
| 64 | 8.61 | 11.86 | 12.08 | 12.29 |
| 65 | 6.54 | 10.77 | 10.98 | 11.20 |
| Pooled: Final denials | ||||
| 18 | 5.02 | 3.79 | 4.02 | 4.26 |
| 19 | 6.16 | 4.46 | 4.71 | 4.96 |
| 20 | 4.83 | 5.21 | 5.48 | 5.76 |
| 21 | 4.16 | 6.01 | 6.29 | 6.58 |
| 22 | 4.79 | 6.84 | 7.14 | 7.45 |
| 23 | 6.64 | 7.67 | 7.97 | 8.29 |
| 24 | 6.66 | 8.60 | 8.91 | 9.24 |
| 25 | 9.26 | 9.32 | 9.64 | 9.96 |
| 26 | 11.60 | 10.22 | 10.54 | 10.87 |
| 27 | 11.60 | 10.92 | 11.24 | 11.56 |
| 28 | 12.16 | 11.56 | 11.88 | 12.19 |
| 29 | 13.14 | 12.16 | 12.47 | 12.78 |
| 30 | 13.60 | 12.65 | 12.95 | 13.25 |
| 31 | 13.15 | 13.12 | 13.41 | 13.70 |
| 32 | 13.90 | 13.57 | 13.85 | 14.14 |
| 33 | 14.24 | 13.91 | 14.19 | 14.47 |
| 34 | 14.44 | 14.23 | 14.50 | 14.77 |
| 35 | 14.65 | 14.48 | 14.75 | 15.02 |
| 36 | 14.57 | 14.61 | 14.88 | 15.14 |
| 37 | 14.53 | 14.63 | 14.89 | 15.15 |
| 38 | 15.15 | 14.73 | 14.99 | 15.26 |
| 39 | 14.55 | 14.72 | 14.97 | 15.23 |
| 40 | 15.54 | 14.66 | 14.91 | 15.17 |
| 41 | 14.92 | 14.44 | 14.69 | 14.94 |
| 42 | 14.64 | 14.25 | 14.50 | 14.75 |
| 43 | 14.52 | 13.96 | 14.20 | 14.45 |
| 44 | 13.87 | 13.64 | 13.88 | 14.12 |
| 45 | 14.14 | 13.27 | 13.50 | 13.73 |
| 46 | 14.94 | 12.90 | 13.12 | 13.35 |
| 47 | 14.67 | 12.54 | 12.75 | 12.98 |
| 48 | 13.79 | 12.04 | 12.25 | 12.46 |
| 49 | 11.80 | 11.49 | 11.69 | 11.89 |
| 50 | 10.59 | 10.94 | 11.13 | 11.33 |
| 51 | 10.32 | 10.32 | 10.51 | 10.69 |
| 52 | 9.89 | 9.69 | 9.86 | 10.03 |
| 53 | 8.65 | 9.12 | 9.28 | 9.44 |
| 54 | 7.53 | 8.50 | 8.65 | 8.81 |
| 55 | 6.05 | 7.82 | 7.97 | 8.11 |
| 56 | 5.87 | 7.13 | 7.26 | 7.40 |
| 57 | 5.87 | 6.51 | 6.64 | 6.77 |
| 58 | 5.49 | 5.88 | 6.00 | 6.12 |
| 59 | 5.11 | 5.31 | 5.43 | 5.55 |
| 60 | 4.85 | 4.72 | 4.83 | 4.94 |
| 61 | 4.69 | 4.16 | 4.27 | 4.37 |
| 62 | 5.07 | 3.86 | 3.96 | 4.07 |
| 63 | 4.10 | 3.12 | 3.22 | 3.31 |
| 64 | 3.92 | 2.76 | 2.85 | 2.94 |
| 65 | 4.19 | 2.60 | 2.70 | 2.79 |
| Diagnosis: Initial allowances | ||||
| 18 | 64.02 | 61.13 | 66.65 | 71.61 |
| 19 | 68.99 | 63.33 | 67.88 | 72.18 |
| 20 | 70.33 | 61.23 | 65.56 | 69.68 |
| 21 | 68.38 | 58.07 | 62.35 | 66.47 |
| 22 | 67.49 | 60.84 | 64.30 | 67.69 |
| 23 | 61.96 | 54.71 | 57.94 | 61.18 |
| 24 | 56.81 | 50.57 | 53.91 | 57.21 |
| 25 | 48.17 | 45.55 | 48.69 | 51.90 |
| 26 | 42.49 | 40.60 | 43.62 | 46.71 |
| 27 | 38.55 | 37.23 | 40.24 | 43.27 |
| 28 | 37.28 | 35.59 | 38.39 | 41.27 |
| 29 | 36.36 | 34.12 | 36.73 | 39.41 |
| 30 | 34.39 | 32.31 | 34.91 | 37.54 |
| 31 | 32.91 | 30.92 | 33.42 | 35.94 |
| 32 | 32.35 | 29.72 | 32.08 | 34.53 |
| 33 | 32.58 | 30.31 | 32.54 | 34.82 |
| 34 | 32.23 | 29.62 | 31.75 | 33.93 |
| 35 | 31.61 | 28.93 | 30.98 | 33.08 |
| 36 | 30.21 | 28.03 | 29.96 | 31.97 |
| 37 | 30.32 | 28.63 | 30.55 | 32.54 |
| 38 | 30.62 | 28.04 | 29.92 | 31.86 |
| 39 | 30.66 | 28.39 | 30.27 | 32.22 |
| 40 | 30.40 | 28.21 | 30.05 | 31.95 |
| 41 | 30.11 | 28.95 | 30.82 | 32.73 |
| 42 | 30.81 | 29.40 | 31.27 | 33.19 |
| 43 | 31.58 | 30.04 | 31.93 | 33.88 |
| 44 | 31.53 | 30.95 | 32.84 | 34.78 |
| 45 | 32.20 | 31.31 | 33.19 | 35.12 |
| 46 | 32.05 | 32.31 | 34.23 | 36.18 |
| 47 | 32.08 | 32.98 | 34.92 | 36.89 |
| 48 | 33.26 | 34.68 | 36.67 | 38.69 |
| 49 | 34.47 | 36.30 | 38.30 | 40.33 |
| 50 | 39.03 | 37.31 | 39.34 | 41.38 |
| 51 | 41.19 | 39.02 | 41.09 | 43.16 |
| 52 | 42.65 | 40.68 | 42.75 | 44.83 |
| 53 | 43.76 | 42.51 | 44.62 | 46.73 |
| 54 | 45.46 | 44.57 | 46.67 | 48.76 |
| 55 | 54.47 | 46.87 | 49.02 | 51.17 |
| 56 | 57.12 | 49.26 | 51.42 | 53.57 |
| 57 | 58.87 | 51.71 | 53.90 | 56.06 |
| 58 | 59.81 | 54.22 | 56.43 | 58.61 |
| 59 | 61.22 | 56.70 | 58.95 | 61.17 |
| 60 | 62.65 | 59.38 | 61.69 | 63.96 |
| 61 | 63.98 | 61.79 | 64.19 | 66.54 |
| 62 | 59.31 | 61.90 | 64.52 | 67.08 |
| 63 | 66.18 | 66.83 | 69.56 | 72.19 |
| 64 | 68.66 | 69.03 | 71.99 | 74.80 |
| 65 | 65.34 | 67.70 | 71.32 | 74.75 |
| Diagnosis: Initial denials not appealed | ||||
| 18 | 28.03 | 21.41 | 26.31 | 31.91 |
| 19 | 20.87 | 20.55 | 24.86 | 29.57 |
| 20 | 20.14 | 21.47 | 25.60 | 30.15 |
| 21 | 22.33 | 23.46 | 27.61 | 32.16 |
| 22 | 22.86 | 21.84 | 25.38 | 29.16 |
| 23 | 24.75 | 25.78 | 29.34 | 33.06 |
| 24 | 27.54 | 27.24 | 30.88 | 34.72 |
| 25 | 31.44 | 29.57 | 33.27 | 37.07 |
| 26 | 33.16 | 31.51 | 35.07 | 38.80 |
| 27 | 35.54 | 32.16 | 35.69 | 39.39 |
| 28 | 34.54 | 31.62 | 35.01 | 38.53 |
| 29 | 32.02 | 31.33 | 34.46 | 37.75 |
| 30 | 31.96 | 30.98 | 33.99 | 37.20 |
| 31 | 32.60 | 30.53 | 33.43 | 36.53 |
| 32 | 31.25 | 29.87 | 32.66 | 35.64 |
| 33 | 30.49 | 28.53 | 31.10 | 33.85 |
| 34 | 29.29 | 27.72 | 30.18 | 32.81 |
| 35 | 30.03 | 26.85 | 29.21 | 31.74 |
| 36 | 29.72 | 26.48 | 28.74 | 31.16 |
| 37 | 29.54 | 25.22 | 27.40 | 29.74 |
| 38 | 28.13 | 24.59 | 26.71 | 28.99 |
| 39 | 27.59 | 23.59 | 25.68 | 27.91 |
| 40 | 27.21 | 23.01 | 25.01 | 27.15 |
| 41 | 26.50 | 21.99 | 23.93 | 26.01 |
| 42 | 25.33 | 21.25 | 23.19 | 25.27 |
| 43 | 25.36 | 20.54 | 22.44 | 24.48 |
| 44 | 24.06 | 19.76 | 21.60 | 23.58 |
| 45 | 22.59 | 19.32 | 21.09 | 22.99 |
| 46 | 22.21 | 18.72 | 20.46 | 22.34 |
| 47 | 22.12 | 18.29 | 20.00 | 21.85 |
| 48 | 21.19 | 17.64 | 19.32 | 21.14 |
| 49 | 19.89 | 16.96 | 18.58 | 20.33 |
| 50 | 17.44 | 16.64 | 18.23 | 19.94 |
| 51 | 17.00 | 16.18 | 17.73 | 19.41 |
| 52 | 16.58 | 15.86 | 17.39 | 19.05 |
| 53 | 16.24 | 15.49 | 17.00 | 18.65 |
| 54 | 15.16 | 15.03 | 16.50 | 18.08 |
| 55 | 12.59 | 14.60 | 16.07 | 17.68 |
| 56 | 11.49 | 14.31 | 15.77 | 17.36 |
| 57 | 11.73 | 13.99 | 15.47 | 17.06 |
| 58 | 11.21 | 13.64 | 15.12 | 16.73 |
| 59 | 11.03 | 13.40 | 14.91 | 16.57 |
| 60 | 11.68 | 13.07 | 14.64 | 16.35 |
| 61 | 12.84 | 12.82 | 14.46 | 16.26 |
| 62 | 22.93 | 13.64 | 15.50 | 17.54 |
| 63 | 19.16 | 11.99 | 13.88 | 15.99 |
| 64 | 18.80 | 11.61 | 13.67 | 16.00 |
| 65 | 23.93 | 12.27 | 14.87 | 17.85 |
| Diagnosis: Final allowances | ||||
| 18 | 2.93 | 1.93 | 3.07 | 4.82 |
| 19 | 3.98 | 2.29 | 3.44 | 5.07 |
| 20 | 4.70 | 3.00 | 4.31 | 6.22 |
| 21 | 5.13 | 3.42 | 4.87 | 6.89 |
| 22 | 4.86 | 3.73 | 5.11 | 6.93 |
| 23 | 6.64 | 4.74 | 6.24 | 8.21 |
| 24 | 8.99 | 5.92 | 7.63 | 9.81 |
| 25 | 11.14 | 7.34 | 9.20 | 11.50 |
| 26 | 12.75 | 9.11 | 11.12 | 13.57 |
| 27 | 14.31 | 10.63 | 12.77 | 15.34 |
| 28 | 16.02 | 12.33 | 14.56 | 17.15 |
| 29 | 18.48 | 13.83 | 16.06 | 18.62 |
| 30 | 20.06 | 15.42 | 17.66 | 20.20 |
| 31 | 21.35 | 16.79 | 19.03 | 21.59 |
| 32 | 22.51 | 18.34 | 20.64 | 23.21 |
| 33 | 22.70 | 19.52 | 21.73 | 24.19 |
| 34 | 24.03 | 20.92 | 23.11 | 25.50 |
| 35 | 23.70 | 22.37 | 24.56 | 26.94 |
| 36 | 25.50 | 23.58 | 25.73 | 28.03 |
| 37 | 25.61 | 24.55 | 26.68 | 28.98 |
| 38 | 26.10 | 25.68 | 27.83 | 30.14 |
| 39 | 27.21 | 26.59 | 28.74 | 31.05 |
| 40 | 26.86 | 27.50 | 29.63 | 31.90 |
| 41 | 28.47 | 28.20 | 30.32 | 32.58 |
| 42 | 29.22 | 28.73 | 30.89 | 33.19 |
| 43 | 28.54 | 29.22 | 31.40 | 33.72 |
| 44 | 30.54 | 29.61 | 31.77 | 34.06 |
| 45 | 31.07 | 30.07 | 32.19 | 34.45 |
| 46 | 30.80 | 30.14 | 32.26 | 34.52 |
| 47 | 31.13 | 30.31 | 32.43 | 34.68 |
| 48 | 31.76 | 29.90 | 32.03 | 34.29 |
| 49 | 33.84 | 29.68 | 31.77 | 34.00 |
| 50 | 32.93 | 29.51 | 31.57 | 33.78 |
| 51 | 31.49 | 28.93 | 30.97 | 33.16 |
| 52 | 30.88 | 28.21 | 30.21 | 32.36 |
| 53 | 31.35 | 27.35 | 29.33 | 31.46 |
| 54 | 31.85 | 26.48 | 28.39 | 30.45 |
| 55 | 26.89 | 25.20 | 27.10 | 29.15 |
| 56 | 25.52 | 23.80 | 25.65 | 27.64 |
| 57 | 23.53 | 22.27 | 24.08 | 26.04 |
| 58 | 23.49 | 20.70 | 22.47 | 24.40 |
| 59 | 22.64 | 18.94 | 20.69 | 22.59 |
| 60 | 20.82 | 17.07 | 18.80 | 20.70 |
| 61 | 18.48 | 15.26 | 16.96 | 18.85 |
| 62 | 12.69 | 13.90 | 15.67 | 17.64 |
| 63 | 10.56 | 11.46 | 13.17 | 15.14 |
| 64 | 8.61 | 9.63 | 11.35 | 13.36 |
| 65 | 6.54 | 8.86 | 10.76 | 13.09 |
| Diagnosis: Final denials | ||||
| 18 | 5.02 | 2.31 | 3.97 | 6.46 |
| 19 | 6.16 | 2.36 | 3.82 | 5.95 |
| 20 | 4.83 | 2.93 | 4.53 | 6.87 |
| 21 | 4.16 | 3.46 | 5.17 | 7.62 |
| 22 | 4.79 | 3.59 | 5.22 | 7.40 |
| 23 | 6.64 | 4.64 | 6.47 | 8.76 |
| 24 | 6.66 | 5.65 | 7.59 | 10.03 |
| 25 | 9.26 | 6.80 | 8.84 | 11.38 |
| 26 | 11.60 | 8.13 | 10.18 | 12.74 |
| 27 | 11.60 | 9.14 | 11.30 | 13.89 |
| 28 | 12.16 | 9.89 | 12.04 | 14.60 |
| 29 | 13.14 | 10.69 | 12.75 | 15.17 |
| 30 | 13.60 | 11.45 | 13.45 | 15.78 |
| 31 | 13.15 | 12.11 | 14.12 | 16.46 |
| 32 | 13.90 | 12.63 | 14.62 | 16.88 |
| 33 | 14.24 | 12.78 | 14.62 | 16.72 |
| 34 | 14.44 | 13.17 | 14.96 | 16.98 |
| 35 | 14.65 | 13.49 | 15.26 | 17.25 |
| 36 | 14.57 | 13.85 | 15.58 | 17.49 |
| 37 | 14.53 | 13.70 | 15.36 | 17.22 |
| 38 | 15.15 | 13.86 | 15.54 | 17.40 |
| 39 | 14.55 | 13.67 | 15.31 | 17.13 |
| 40 | 15.54 | 13.72 | 15.31 | 17.08 |
| 41 | 14.92 | 13.37 | 14.94 | 16.67 |
| 42 | 14.64 | 13.10 | 14.65 | 16.38 |
| 43 | 14.52 | 12.70 | 14.23 | 15.93 |
| 44 | 13.87 | 12.31 | 13.79 | 15.44 |
| 45 | 14.14 | 12.09 | 13.53 | 15.12 |
| 46 | 14.94 | 11.66 | 13.05 | 14.61 |
| 47 | 14.67 | 11.29 | 12.65 | 14.17 |
| 48 | 13.79 | 10.66 | 11.98 | 13.46 |
| 49 | 11.80 | 10.09 | 11.35 | 12.76 |
| 50 | 10.59 | 9.66 | 10.86 | 12.21 |
| 51 | 10.32 | 9.06 | 10.22 | 11.51 |
| 52 | 9.89 | 8.53 | 9.65 | 10.90 |
| 53 | 8.65 | 7.98 | 9.05 | 10.25 |
| 54 | 7.53 | 7.44 | 8.44 | 9.57 |
| 55 | 6.05 | 6.83 | 7.80 | 8.91 |
| 56 | 5.87 | 6.23 | 7.15 | 8.20 |
| 57 | 5.87 | 5.67 | 6.56 | 7.58 |
| 58 | 5.49 | 5.12 | 5.97 | 6.96 |
| 59 | 5.11 | 4.62 | 5.45 | 6.42 |
| 60 | 4.85 | 4.07 | 4.87 | 5.82 |
| 61 | 4.69 | 3.60 | 4.39 | 5.34 |
| 62 | 5.07 | 3.46 | 4.31 | 5.35 |
| 63 | 4.10 | 2.63 | 3.39 | 4.37 |
| 64 | 3.92 | 2.23 | 2.99 | 3.98 |
| 65 | 4.19 | 2.15 | 3.05 | 4.29 |
In general, it appears that the square term for age does a reasonably good job at capturing the nonlinear shape of the age profiles. The left and right columns of graphs in Chart 7 correspond to the pooled and hierarchical diagnosis models, respectively. The interval estimates for the pooled specification seem inadequately narrow, seriously underrepresenting uncertainty, as they miss most of the actual proportions. The point and interval predictions for the hierarchical diagnosis process clearly provide an improvement in fit. This is particularly evident in both the greater width of the intervals and at the youngest ages, where the shape of the age profiles is defined by relatively small numbers of claimants with a predominance of mental impairments.
Variance Decomposition
One issue of particular interest in this analysis is variance decomposition; that is, the portion of total variation in outcomes that the models attribute to the groups rather than the claimants. The top panel of Table 7 presents posterior means and standard deviations of between-group variances for the specifications with intercepts only. Consider for instance the first entry in the table, which corresponds to an initial allowance in the state hierarchical specification. The model has 50 intercept parameters per equation, each representing a state's mean linear prediction of an initial allowance. The posterior mean of the variance among those predictions is 0.22. Likewise, the between-state variance estimate for the linear prediction of an initial denial not appealed is 0.16.
| Disability outcome | State | Diagnosis | ||
|---|---|---|---|---|
| Mean | Standard deviation | Mean | Standard deviation | |
| Between-group variances: Intercepts only | ||||
| Initial allowances | 0.219 | 0.044 | 2.587 | 0.286 |
| Initial denials not appealed | 0.160 | 0.032 | 0.122 | 0.016 |
| Final allowances | 0.180 | 0.036 | 0.269 | 0.035 |
| Between-group variances: Individual-level inputs | ||||
| Initial allowances | 0.594 | 0.120 | 2.824 | 0.338 |
| Initial denials not appealed | 0.514 | 0.104 | 0.274 | 0.034 |
| Final allowances | 0.543 | 0.108 | 0.409 | 0.052 |
| ICCs (percent) | ||||
| Initial allowances | 6.22 | 1.17 | 43.89 | 2.70 |
| Initial denials not appealed | 4.65 | 0.90 | 3.59 | 0.46 |
| Final allowances | 5.17 | 0.98 | 7.56 | 0.91 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | ||||
| NOTE: ICC = intraclass correlation coefficient. | ||||
In a similar fashion, the middle panel of Table 7 shows between-group variances corresponding to the models with claimant-level explanatory variables. Now the intercepts represent mean linear predictions of the outcomes when the explanatory variables take their average values in the sample.15 Thus, the adjusted mean linear prediction of an initial allowance has a between-state variance of 0.59. Likewise, the variance of the mean-adjusted predictions for an initial denial not appealed between the states is 0.51.
One pattern emerges from the estimates in Table 7. For a given specification, the between-state variances corresponding to the prediction of all three outcomes are small and close in magnitude to one another. On the other hand, things are quite different when claimants are grouped by their impairments. In particular, variation in the prediction of an initial allowance between the diagnoses is very large (2.6 for the model with only intercepts and 2.8 for the variant with individual explanatory variables). Those magnitudes dwarf the variances associated with the other adjudicative categories (initial denials not appealed and final allowances). The implication is one of considerable heterogeneity in the prediction of an initial allowance among the impairments. This is of course consistent with the description of the data, where some primary diagnosis codes have initial allowance rates of over 95 percent, while others are close to zero.
In hierarchical models, total data variance is the sum of the within-group and the between-group variances. A useful statistic of variance decomposition is the intraclass correlation coefficient (ICC), which measures the proportion of variance in the outcomes between the groups. A value close to zero indicates a good deal of homogeneity between the clusters, so that most of the data variance can be attributed to individual-level variation within the groups. Conversely, an ICC close to 100 percent suggests a high degree of between-group heterogeneity, which implicitly favors a hierarchical modeling structure.
The bottom panel of Table 7 displays estimated ICC values.16 On average, only about 6.2 percent of total variance in initial allowances can be attributed to differences between the states. Most of the observed heterogeneity in initial allowances (over 90 percent) seems to be due to disparities among claimants within the states. The decomposition suggests that applicants within any given state can be very heterogeneous in their disability characteristics. In fact, once claimants are grouped by primary diagnosis, a large portion of variation previously attributed to the individuals can now be explained by the differences between the impairments. About 44 percent of total variation in initial allowances is attributed to the different diagnosis groups. These results do not extend to the other outcomes (initial denials not appealed and final allowances), where group-level heterogeneity does not exceed 10 percent of total variance.
One of the implications of the ICC estimates is that the primary diagnoses can account for a great deal of the observed variation in initial allowances among claimants. To the extent that it is possible, parallels are drawn between the findings in this article and those in Rupp (2012). Fixed-effects models are not designed to apportion variance into between-group and within-group sources. Rupp (2012, Table 9) looked at the decomposition of overall variation in initial allowance rates across states by three sources. For adult DI-only claimants, the state fixed-effects accounted for 52 percent of the variation, while the year fixed-effects and the demographic and diagnostic characteristics of claimants contributed 14 percent and 10 percent of variation, respectively. The large size of the state fixed-effects in Rupp's article suggested that long-term unique differences among the states were substantial. That might seem at odds with this article's finding of small between-state, but large within-state variation in the outcomes. Notice, however, that the hierarchical state model here tracks with a great deal of accuracy the four adjudicative outcomes for each one of the states. This is by design because the model accommodates state-specific parameters. In other words, the hierarchical state model does a much better job at predicting the observed allowance and denial rates by state than does the hierarchical diagnosis model. Nevertheless, as the DIC tabulation and Table 5 confirm, the hierarchical diagnosis model unquestionably fits the overall data much better. First, it yields a significantly smaller DIC estimate. Second, for all claimants, it correctly predicts a higher share of each of the four adjudicative outcomes than does the state model.
The results in Rupp (2012) hinted at the diagnostic mix playing a role (although a small one), in explaining state heterogeneity in initial allowance rates.17 The findings here (values not shown) are consistent with that view, in that the diagnostic mix is not a major factor at accurately predicting initial allowance rates in most states, except in some cases, despite the fact that state variation in the composition of impairments is substantial in the sample under study. For instance, the proportion of musculoskeletal diagnoses ranges from 27 percent in Hawaii to 42.9 percent in Montana. Mental disorders comprise 26.9 percent of the diagnoses in New Hampshire, but only 12.1 percent of those in Arkansas. Neoplasms vary from 13.6 percent in Iowa to 6.3 percent in West Virginia. Mississippi has the highest composition of circulatory diagnoses at 15.8 percent, while Idaho has the lowest at 7.1 percent. For the nervous system and sense organs group, Colorado has a proportion of diagnoses (12.3 percent) that is three times the size of that corresponding to Vermont. Injuries also vary from 2.5 percent in South Dakota to 10.6 percent in West Virginia. Coe and others (2011) cited substantial variation in age-adjusted mortality rates by state and even greater variation in self-reported disability.
In the context of my modeling effort, one way to further illustrate state heterogeneity in disability outcomes is through a specific example. Chart 8 provides a comparison between the states of Hawaii and West Virginia. The graphs display point and interval probability predictions (90 percent posterior probability) of an initial allowance as a function of earnings for both states. Hawaii exhibits the highest initial allowance rate in the sample at 62.5 percent. In addition, it also happens to have the lowest proportion of musculoskeletal impairments of any state. By contrast, West Virginia has the third-lowest initial allowance rate (37.4 percent) and incidentally, the lowest proportion of neoplasms and the highest share of injuries among the 50 states.
Aggregate point and interval probability predictions for an initial allowance, by earnings: Hawaii compared with West Virginia
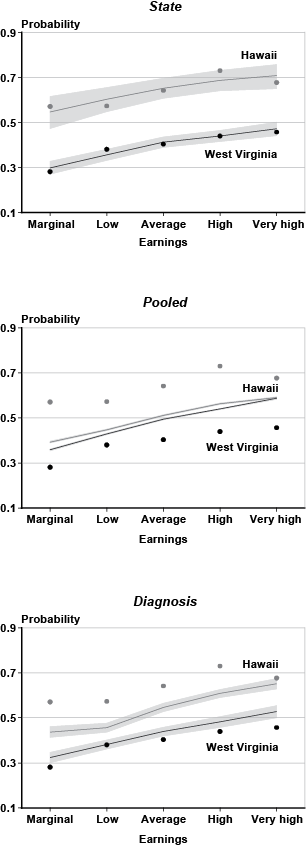
| Earnings | Hawaii | West Virginia | ||||||
|---|---|---|---|---|---|---|---|---|
| Actual | 5th percentile | 50th percentile | 95th percentile | Actual | 5th percentile | 50th percentile | 95th percentile | |
| State | ||||||||
| Marginal | 57.10 | 47.37 | 54.59 | 61.54 | 28.14 | 27.00 | 29.82 | 32.75 |
| Low | 57.31 | 54.84 | 60.22 | 65.44 | 38.02 | 33.21 | 35.62 | 38.08 |
| Average | 64.20 | 60.68 | 65.13 | 69.56 | 40.36 | 38.92 | 41.21 | 43.55 |
| High | 73.02 | 64.08 | 68.70 | 73.08 | 43.95 | 41.52 | 43.98 | 46.43 |
| Very high | 67.71 | 65.08 | 70.80 | 75.73 | 45.70 | 44.19 | 47.11 | 50.05 |
| Diagnosis | ||||||||
| Marginal | 57.10 | 41.33 | 43.69 | 46.04 | 28.14 | 30.06 | 32.35 | 34.72 |
| Low | 57.31 | 43.63 | 45.64 | 47.65 | 38.02 | 36.17 | 38.16 | 40.22 |
| Average | 64.20 | 52.83 | 54.68 | 56.52 | 40.36 | 42.05 | 43.94 | 45.87 |
| High | 73.02 | 59.05 | 60.84 | 62.59 | 43.95 | 45.87 | 48.18 | 50.60 |
| Very high | 67.71 | 62.91 | 65.22 | 67.42 | 45.70 | 50.07 | 52.75 | 55.39 |
| Pooled | ||||||||
| Marginal | 57.10 | 38.99 | 39.33 | 39.68 | 28.14 | 35.52 | 35.85 | 36.19 |
| Low | 57.31 | 44.49 | 44.77 | 45.06 | 38.02 | 42.62 | 42.90 | 43.18 |
| Average | 64.20 | 50.88 | 51.15 | 51.41 | 40.36 | 49.23 | 49.49 | 49.75 |
| High | 73.02 | 56.01 | 56.30 | 56.58 | 43.95 | 53.68 | 53.96 | 54.22 |
| Very high | 67.71 | 58.77 | 59.11 | 59.44 | 45.70 | 58.37 | 58.69 | 58.99 |
The top graph in Chart 8 corresponds to the hierarchical state model, which by design, accurately reproduces the observed state proportions. Notice that Hawaii has a smaller number of observations than West Virginia (Appendix Table A-2), resulting in state-specific parameter estimates with greater variance (and as a result, a wider probability interval). The middle graph in Chart 8 presents the predictions associated with the pooled model. In this case, there is a wide gap between observed and predicted outcomes. Over all claimants, Hawaii and West Virginia differ in their proportion of initial allowances by about 25 percentage points (see Chart 1). Instead, the pooled model predicts a mean gap of about 3 percentage points, despite the fact that the predictions take into account the different mix of characteristics between the applicant populations in the two states (age, sex, employment status, application history, and earnings history).
The graph at the bottom of Chart 8 shows the probability predictions resulting from the hierarchical diagnosis model. This specification incorporates the same individual-level predictors as the pooled multinomial logit model. The only difference, of course, is that claimants are grouped according to their impairments. Relative to the observed proportions, the diagnosis model slightly overpredicts the probabilities corresponding to West Virginia, but significantly underpredicts the probabilities associated with Hawaii. On average, the predicted gap in the probability of an initial allowance between the two states is 11 percentage points. In other words, discrepancies in claimant-level characteristics (differences in the impairment mix specifically) seem to account for a little less than half of the observed difference in the initial allowance rate between these two states. This result, however, does not generalize to comparisons among other states.
Correlation Across Outcomes
Table 8 presents posterior estimates of the correlation between the disability adjudicative outcomes. The top panel of the table corresponds to the intercepts-only specification, while the bottom panel comprises the estimates for the models with claimant-level predictors. For example, the mean correlation between the average linear predictions of an initial allowance and an initial denial not appealed among the 50 states is 0.25. Likewise, the mean correlation between those two outcomes among the 181 primary diagnosis codes is 0.31. When the individual explanatory variables are included in the models, the corresponding correlation for the adjusted linear prediction of an initial allowance and an initial denial not appealed is 0.1 among the states and 0.13 among the impairments.
| Correlation sequence of disability outcome | State | Diagnosis | ||
|---|---|---|---|---|
| Mean | Standard deviation | Mean | Standard deviation | |
| Intercepts only | ||||
| Initial allowance—initial denial not appealed | 0.249 | 0.129 | 0.307 | 0.087 |
| Initial allowance—final allowance | 0.063 | 0.136 | 0.737 | 0.041 |
| Initial denial not appealed—final allowance | 0.015 | 0.135 | 0.177 | 0.092 |
| Individual-level inputs | ||||
| Initial allowance—initial denial not appealed | 0.100 | 0.133 | 0.125 | 0.096 |
| Initial allowance—final allowance | 0.048 | 0.135 | 0.561 | 0.064 |
| Initial denial not appealed—final allowance | 0.006 | 0.134 | 0.119 | 0.087 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | ||||
A look at Table 8 reveals that after controlling for individual-level predictors, the correlations in the state hierarchical models are small in magnitude and statistically insignificant. However, when claimants are grouped by diagnosis, there is very high statistically significant positive correlation between the linear predictions of an initial and a final allowance. For instance, with only intercepts, the posterior mean correlation among the impairments is 0.74. After controlling for claimant-level explanatory variables, a mean estimate of 0.56 is obtained. To the best of my knowledge, the finding of high significant positive correlation when impairments are used as a criterion for grouping claimants has never been reported in the literature. The finding is important for several reasons. First, it indicates that the zero correlation property implicit in a pure multinomial logit model (the so-called independence from irrelevant alternatives property) is an unrealistic restriction. More generally, any effort to model the adjudicative process using the impairments should accommodate this pattern in the data.
My classification of claimants roughly corresponds to a two-stage adjudication (decisions at the DDS level versus decisions made mostly at the hearing level or above). In this context, the estimation results suggest a substantial degree of dependence between the two adjudicative outcomes. Across the impairments, the high positive correlation between the predictions of an initial and a final allowance is important for a second reason. Normatively speaking, the more disabling a diagnosis, the greater the linear predictions of both an initial and a final allowance should be, relative to less disabling impairments. In this very narrow sense, the correlation result here appears to suggest a degree of consistency within the adjudicative process.
Consider the top graph on the left in Chart 9, which plots posterior means of the intercepts for the 181 primary diagnosis codes corresponding to the model with claimant-level predictors. Those coefficients represent adjusted mean linear predictions of an initial denial not appealed and a final allowance. There is no apparent relationship between the two outcomes, as a statistically insignificant mean correlation estimate of 0.12 bears out in Table 8. Transforming the linear predictions into actual probabilities results in the top graph on the right. Unlike the linear predictions, the probabilities show an upward trend. Impairments that have a higher classification probability of an initial denial not appealed also tend to have a higher probability of a final allowance.
Linear predictions compared with probabilities in the diagnosis model
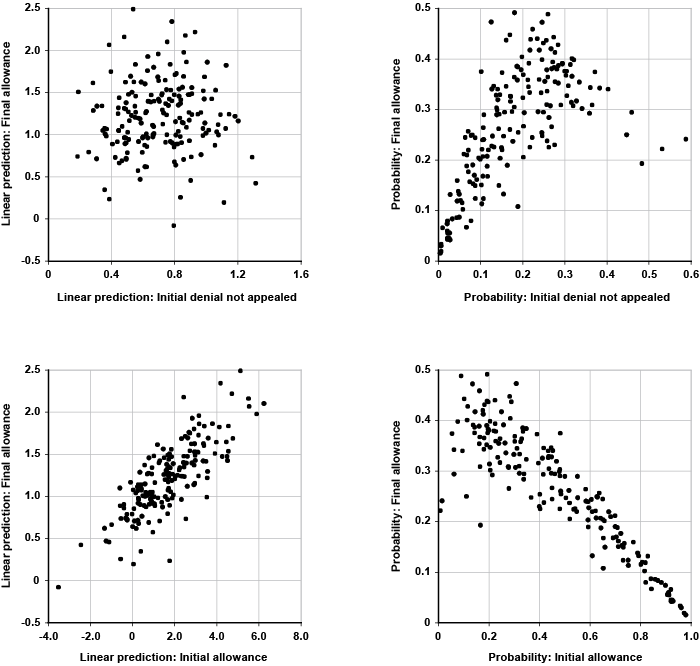
| Diagnosis | Linear prediction | Probability | ||||
|---|---|---|---|---|---|---|
| Initial allowance | Initial denial not appealed | Final allowance | Initial allowance | Initial denial not appealed | Final allowance | |
| 1 | 1.4255 | 1.0552 | 0.8749 | 0.3988 | 0.2754 | 0.2300 |
| 2 | 2.9709 | 0.9092 | 1.4879 | 0.7115 | 0.0905 | 0.1615 |
| 3 | -0.5453 | 0.9054 | 0.7369 | 0.0944 | 0.4026 | 0.3402 |
| 4 | 1.7564 | 0.5300 | 1.5041 | 0.4458 | 0.1308 | 0.3464 |
| 5 | 1.7606 | 0.4861 | 0.8939 | 0.5342 | 0.1493 | 0.2245 |
| 6 | 0.9883 | 0.4373 | 0.9167 | 0.3473 | 0.2002 | 0.3233 |
| 7 | 1.3841 | 0.8934 | 0.9296 | 0.4004 | 0.2451 | 0.2542 |
| 8 | 2.9502 | 0.5885 | 1.6261 | 0.7079 | 0.0667 | 0.1883 |
| 9 | 3.5957 | 0.8566 | 1.6920 | 0.8058 | 0.0521 | 0.1201 |
| 10 | 1.5853 | 0.4898 | 1.3051 | 0.4357 | 0.1457 | 0.3293 |
| 11 | 5.5099 | 0.4811 | 2.1617 | 0.9563 | 0.0063 | 0.0336 |
| 12 | 4.4896 | 0.8931 | 1.4753 | 0.9194 | 0.0252 | 0.0451 |
| 13 | 3.5638 | 0.7229 | 1.2960 | 0.8402 | 0.0490 | 0.0870 |
| 14 | 3.1343 | 1.1446 | 1.2431 | 0.7512 | 0.1027 | 0.1134 |
| 15 | 5.5386 | 0.3854 | 2.0682 | 0.9608 | 0.0056 | 0.0299 |
| 16 | 4.5540 | 0.7481 | 1.5360 | 0.9245 | 0.0206 | 0.0452 |
| 17 | 5.8964 | 0.8579 | 1.9788 | 0.9717 | 0.0063 | 0.0193 |
| 18 | 3.4906 | 0.8390 | 1.4155 | 0.8153 | 0.0575 | 0.1024 |
| 19 | 4.7648 | 0.9894 | 1.6882 | 0.9280 | 0.0213 | 0.0428 |
| 20 | 4.2633 | 0.7189 | 1.4742 | 0.9054 | 0.0262 | 0.0557 |
| 21 | 4.5575 | 0.7719 | 1.8359 | 0.9100 | 0.0207 | 0.0598 |
| 22 | 3.7943 | 0.8751 | 1.8639 | 0.8186 | 0.0442 | 0.1188 |
| 23 | 3.5494 | 1.1826 | 1.2203 | 0.8197 | 0.0769 | 0.0798 |
| 24 | 4.5138 | 0.9873 | 1.4253 | 0.9209 | 0.0271 | 0.0420 |
| 25 | 2.6023 | 1.0755 | 1.1203 | 0.6585 | 0.1431 | 0.1496 |
| 26 | 2.5323 | 1.2910 | 0.7336 | 0.6519 | 0.1884 | 0.1079 |
| 27 | 2.8185 | 0.7036 | 1.3971 | 0.7034 | 0.0849 | 0.1698 |
| 28 | 3.0745 | 0.7756 | 1.5304 | 0.7352 | 0.0738 | 0.1570 |
| 29 | 3.5243 | 0.9792 | 0.9910 | 0.8422 | 0.0661 | 0.0669 |
| 30 | 3.9832 | 0.6982 | 1.6436 | 0.8677 | 0.0325 | 0.0836 |
| 31 | 4.4569 | 0.7405 | 1.6470 | 0.9123 | 0.0222 | 0.0549 |
| 32 | 3.3674 | 0.5415 | 1.6268 | 0.7879 | 0.0467 | 0.1382 |
| 33 | 2.0246 | 0.9463 | 1.2430 | 0.5182 | 0.1763 | 0.2371 |
| 34 | 3.3935 | 0.6123 | 1.6043 | 0.7920 | 0.0491 | 0.1323 |
| 35 | 3.1107 | 0.9816 | 1.5222 | 0.7311 | 0.0870 | 0.1493 |
| 36 | 6.2423 | 0.7532 | 2.1031 | 0.9785 | 0.0040 | 0.0156 |
| 37 | 2.9574 | 0.8059 | 1.1561 | 0.7500 | 0.0872 | 0.1238 |
| 38 | 2.3795 | 1.0901 | 1.2397 | 0.5924 | 0.1632 | 0.1895 |
| 39 | 4.1822 | 0.7823 | 2.3445 | 0.8279 | 0.0276 | 0.1318 |
| 40 | 4.1237 | 1.1261 | 1.8247 | 0.8573 | 0.0428 | 0.0860 |
| 41 | 1.4916 | 0.6157 | 1.2593 | 0.4108 | 0.1711 | 0.3257 |
| 42 | 1.9348 | 0.6486 | 1.3892 | 0.4999 | 0.1381 | 0.2897 |
| 43 | -0.4068 | 0.6244 | 0.8607 | 0.1129 | 0.3166 | 0.4010 |
| 44 | -0.4092 | 0.4930 | 0.9050 | 0.1150 | 0.2836 | 0.4281 |
| 45 | 0.2917 | 0.6300 | 0.9636 | 0.1958 | 0.2746 | 0.3833 |
| 46 | 0.5549 | 0.8187 | 0.8908 | 0.2339 | 0.3045 | 0.3273 |
| 47 | 0.9129 | 0.5528 | 1.2669 | 0.2838 | 0.1980 | 0.4043 |
| 48 | 1.5592 | 1.0780 | 0.9977 | 0.4169 | 0.2577 | 0.2378 |
| 49 | 2.8013 | 0.4885 | 1.6242 | 0.6813 | 0.0674 | 0.2099 |
| 50 | 0.8639 | 0.6623 | 0.9755 | 0.2979 | 0.2435 | 0.3331 |
| 51 | -0.0208 | 0.5952 | 0.7900 | 0.1633 | 0.3024 | 0.3675 |
| 52 | 3.3567 | 0.6977 | 1.4212 | 0.8005 | 0.0560 | 0.1155 |
| 53 | 2.2174 | 0.4810 | 1.3133 | 0.5917 | 0.1042 | 0.2396 |
| 54 | 1.4624 | 0.8496 | 1.5637 | 0.3472 | 0.1881 | 0.3842 |
| 55 | 1.2071 | 0.3673 | 0.9830 | 0.3952 | 0.1707 | 0.3159 |
| 56 | 2.3083 | 0.9095 | 1.2407 | 0.5917 | 0.1461 | 0.2034 |
| 57 | 3.9143 | 0.1901 | 1.5091 | 0.8816 | 0.0213 | 0.0796 |
| 58 | 1.9444 | 0.9982 | 1.0181 | 0.5189 | 0.2014 | 0.2055 |
| 59 | 0.5969 | 0.8469 | 1.1484 | 0.2188 | 0.2809 | 0.3798 |
| 60 | 0.7785 | 0.8282 | 1.4584 | 0.2230 | 0.2344 | 0.4402 |
| 61 | 1.6740 | 0.4911 | 0.9615 | 0.5040 | 0.1544 | 0.2472 |
| 62 | 3.1525 | 0.6961 | 1.9591 | 0.6985 | 0.0599 | 0.2118 |
| 63 | 2.9788 | 1.0347 | 1.4266 | 0.7114 | 0.1018 | 0.1507 |
| 64 | 1.6689 | 0.7303 | 1.2590 | 0.4458 | 0.1744 | 0.2959 |
| 65 | 2.9211 | 0.6674 | 1.8007 | 0.6734 | 0.0707 | 0.2196 |
| 66 | 1.6442 | 0.5681 | 1.1993 | 0.4598 | 0.1567 | 0.2947 |
| 67 | 1.2864 | 0.8569 | 0.7075 | 0.4020 | 0.2616 | 0.2253 |
| 68 | -3.5170 | 0.7940 | -0.0786 | 0.0071 | 0.5310 | 0.2219 |
| 69 | -2.4512 | 1.3134 | 0.4242 | 0.0136 | 0.5872 | 0.2413 |
| 70 | 2.4288 | 0.8682 | 2.1787 | 0.4815 | 0.1011 | 0.3750 |
| 71 | 2.4319 | 0.6342 | 1.3998 | 0.6212 | 0.1029 | 0.2213 |
| 72 | 0.3927 | 0.3564 | 0.3473 | 0.2782 | 0.2682 | 0.2658 |
| 73 | 0.0438 | 1.1127 | 0.1959 | 0.1657 | 0.4827 | 0.1930 |
| 74 | 3.1629 | 1.0069 | 1.8617 | 0.6992 | 0.0810 | 0.1903 |
| 75 | 0.6009 | 0.6643 | 1.0050 | 0.2432 | 0.2591 | 0.3643 |
| 76 | 2.4490 | 0.7606 | 1.3485 | 0.6235 | 0.1152 | 0.2074 |
| 77 | 2.7228 | 0.8279 | 1.5428 | 0.6565 | 0.0987 | 0.2017 |
| 78 | 2.8352 | 0.6300 | 1.9283 | 0.6358 | 0.0701 | 0.2567 |
| 79 | 5.1275 | 0.5377 | 2.4918 | 0.9193 | 0.0093 | 0.0659 |
| 80 | 3.4105 | 0.5514 | 1.8348 | 0.7709 | 0.0442 | 0.1595 |
| 81 | 1.8441 | 0.9088 | 1.5597 | 0.4342 | 0.1704 | 0.3267 |
| 82 | 2.6819 | 0.6281 | 1.7615 | 0.6269 | 0.0804 | 0.2497 |
| 83 | 2.9262 | 0.7434 | 1.3706 | 0.7260 | 0.0818 | 0.1532 |
| 84 | 0.1745 | 0.6225 | 0.6186 | 0.2014 | 0.3153 | 0.3141 |
| 85 | 0.4940 | 0.6209 | 1.0085 | 0.2263 | 0.2570 | 0.3786 |
| 86 | 0.8589 | 0.4841 | 0.9649 | 0.3103 | 0.2133 | 0.3450 |
| 87 | -0.2708 | 0.4239 | 0.7313 | 0.1421 | 0.2846 | 0.3870 |
| 88 | 1.7227 | 0.4488 | 1.4394 | 0.4522 | 0.1265 | 0.3406 |
| 89 | 0.9494 | 0.3454 | 1.0510 | 0.3289 | 0.1798 | 0.3641 |
| 90 | 2.7259 | 0.3963 | 1.7500 | 0.6495 | 0.0632 | 0.2448 |
| 91 | 1.8103 | 1.0158 | 1.0554 | 0.4795 | 0.2167 | 0.2254 |
| 92 | 2.4379 | 0.8870 | 1.4777 | 0.5945 | 0.1261 | 0.2276 |
| 93 | 0.9650 | 0.5676 | 0.5745 | 0.3663 | 0.2462 | 0.2479 |
| 94 | 0.4462 | 0.9674 | 0.7641 | 0.2128 | 0.3584 | 0.2925 |
| 95 | 0.9102 | 0.7731 | 0.9194 | 0.3045 | 0.2655 | 0.3074 |
| 96 | 2.3226 | 0.5973 | 0.9639 | 0.6522 | 0.1162 | 0.1676 |
| 97 | 2.6057 | 0.7974 | 1.4756 | 0.6407 | 0.1050 | 0.2070 |
| 98 | 0.3738 | 0.7848 | 0.9036 | 0.2043 | 0.3081 | 0.3470 |
| 99 | 0.6278 | 0.4463 | 1.0492 | 0.2570 | 0.2143 | 0.3916 |
| 100 | -0.5637 | 0.8371 | 0.2567 | 0.1100 | 0.4466 | 0.2500 |
| 101 | 1.7588 | 0.3867 | 0.2354 | 0.6083 | 0.1543 | 0.1326 |
| 102 | 0.2780 | 0.7247 | 1.1261 | 0.1768 | 0.2764 | 0.4129 |
| 103 | 0.2938 | 0.4810 | 0.9654 | 0.2037 | 0.2457 | 0.3987 |
| 104 | 1.7324 | 0.5270 | 1.2297 | 0.4805 | 0.1439 | 0.2906 |
| 105 | -1.3295 | 0.6126 | 0.6210 | 0.0532 | 0.3712 | 0.3744 |
| 106 | 0.2722 | 0.5883 | 1.1391 | 0.1814 | 0.2488 | 0.4316 |
| 107 | 1.0143 | 0.5078 | 1.4804 | 0.2810 | 0.1693 | 0.4478 |
| 108 | 0.4273 | 0.8751 | 1.0879 | 0.1941 | 0.3037 | 0.3757 |
| 109 | 0.6999 | 0.8911 | 1.2652 | 0.2239 | 0.2710 | 0.3940 |
| 110 | 0.9249 | 0.3401 | 1.3425 | 0.2880 | 0.1605 | 0.4373 |
| 111 | 3.1341 | 0.8115 | 1.7279 | 0.7212 | 0.0707 | 0.1767 |
| 112 | 0.2359 | 0.6605 | 1.1141 | 0.1747 | 0.2671 | 0.4203 |
| 113 | 1.6293 | 0.4439 | 1.3200 | 0.4473 | 0.1367 | 0.3283 |
| 114 | 0.2399 | 0.3690 | 1.0674 | 0.1919 | 0.2183 | 0.4389 |
| 115 | 2.5022 | 0.8015 | 1.7129 | 0.5819 | 0.1062 | 0.2642 |
| 116 | 2.5538 | 0.6314 | 1.3962 | 0.6501 | 0.0951 | 0.2043 |
| 117 | 1.2527 | 0.6697 | 1.3982 | 0.3333 | 0.1860 | 0.3855 |
| 118 | 2.6217 | 0.5216 | 1.6945 | 0.6286 | 0.0770 | 0.2487 |
| 119 | 2.4669 | 0.7488 | 1.2361 | 0.6425 | 0.1153 | 0.1877 |
| 120 | 1.1840 | 0.2829 | 1.6151 | 0.3076 | 0.1249 | 0.4733 |
| 121 | 0.9095 | 0.3599 | 1.0093 | 0.3242 | 0.1871 | 0.3582 |
| 122 | 2.4202 | 0.7823 | 1.4031 | 0.6079 | 0.1182 | 0.2199 |
| 123 | 1.7981 | 0.5482 | 1.3392 | 0.4798 | 0.1375 | 0.3032 |
| 124 | -0.5839 | 0.4061 | 0.8895 | 0.1015 | 0.2733 | 0.4431 |
| 125 | 2.0086 | 0.5490 | 1.2084 | 0.5507 | 0.1280 | 0.2474 |
| 126 | 0.0903 | 0.4936 | 0.7080 | 0.1899 | 0.2843 | 0.3522 |
| 127 | 1.8673 | 0.5798 | 1.1893 | 0.5159 | 0.1424 | 0.2619 |
| 128 | 2.2478 | 0.3080 | 1.3400 | 0.6050 | 0.0870 | 0.2441 |
| 129 | -0.0898 | 0.5137 | 1.1675 | 0.1344 | 0.2458 | 0.4727 |
| 130 | -0.2665 | 0.5007 | 0.7871 | 0.1365 | 0.2939 | 0.3914 |
| 131 | 0.9037 | 0.5096 | 0.9441 | 0.3205 | 0.2161 | 0.3337 |
| 132 | 0.8540 | 0.5023 | 1.0292 | 0.3011 | 0.2118 | 0.3588 |
| 133 | 1.0260 | 0.8081 | 0.9963 | 0.3191 | 0.2566 | 0.3098 |
| 134 | -0.9953 | 0.4493 | 0.6647 | 0.0757 | 0.3211 | 0.3983 |
| 135 | -0.6013 | 0.4679 | 1.0998 | 0.0891 | 0.2597 | 0.4885 |
| 136 | 0.7590 | 0.6215 | 1.2764 | 0.2489 | 0.2170 | 0.4176 |
| 137 | 0.2700 | 0.5714 | 0.9196 | 0.1988 | 0.2687 | 0.3807 |
| 138 | 0.1546 | 0.8234 | 1.0403 | 0.1604 | 0.3131 | 0.3890 |
| 139 | 1.7152 | 0.6671 | 1.0970 | 0.4832 | 0.1694 | 0.2604 |
| 140 | 1.5443 | 0.8322 | 1.1995 | 0.4145 | 0.2034 | 0.2936 |
| 141 | 2.3262 | 0.6936 | 1.6860 | 0.5494 | 0.1074 | 0.2896 |
| 142 | 4.7175 | 0.9290 | 2.2196 | 0.8978 | 0.0203 | 0.0739 |
| 143 | 0.2719 | 0.8357 | 0.9796 | 0.1802 | 0.3167 | 0.3657 |
| 144 | 1.6940 | 0.8930 | 1.1732 | 0.4491 | 0.2016 | 0.2668 |
| 145 | 0.5720 | 0.8370 | 1.3719 | 0.1963 | 0.2559 | 0.4369 |
| 146 | 1.0598 | 1.2029 | 1.1637 | 0.2770 | 0.3196 | 0.3073 |
| 147 | 0.6437 | 0.6102 | 0.8760 | 0.2664 | 0.2576 | 0.3361 |
| 148 | 1.6238 | 0.4927 | 1.3804 | 0.4341 | 0.1401 | 0.3403 |
| 149 | 1.8513 | 0.6515 | 1.4722 | 0.4667 | 0.1406 | 0.3194 |
| 150 | 0.8487 | 0.4454 | 1.0519 | 0.3011 | 0.2011 | 0.3689 |
| 151 | 0.6002 | 0.7505 | 1.0004 | 0.2379 | 0.2765 | 0.3550 |
| 152 | 1.2994 | 0.7663 | 1.4244 | 0.3341 | 0.1961 | 0.3787 |
| 153 | 0.0342 | 0.3564 | 1.0777 | 0.1617 | 0.2231 | 0.4590 |
| 154 | -0.2533 | 0.4930 | 0.7201 | 0.1420 | 0.2994 | 0.3757 |
| 155 | 1.9072 | 0.9662 | 1.2637 | 0.4844 | 0.1891 | 0.2546 |
| 156 | 0.7110 | 0.6702 | 1.0136 | 0.2628 | 0.2523 | 0.3557 |
| 157 | 0.2513 | 0.3058 | 0.7150 | 0.2261 | 0.2387 | 0.3594 |
| 158 | 2.1363 | 0.4416 | 1.2507 | 0.5834 | 0.1071 | 0.2406 |
| 159 | 1.7112 | 0.8240 | 1.3525 | 0.4365 | 0.1797 | 0.3049 |
| 160 | 0.4230 | 0.8557 | 1.1392 | 0.1907 | 0.2940 | 0.3903 |
| 161 | 1.5018 | 0.5529 | 1.4592 | 0.3894 | 0.1507 | 0.3731 |
| 162 | -0.3194 | 0.1850 | 0.7423 | 0.1444 | 0.2392 | 0.4176 |
| 163 | 1.6678 | 0.2554 | 0.7941 | 0.5406 | 0.1317 | 0.2257 |
| 164 | 2.9417 | 1.0594 | 1.5284 | 0.6904 | 0.1051 | 0.1680 |
| 165 | 0.0059 | 0.8068 | 0.6412 | 0.1637 | 0.3646 | 0.3090 |
| 166 | 0.7937 | 0.8438 | 0.9062 | 0.2761 | 0.2902 | 0.3089 |
| 167 | 0.0664 | 0.7962 | 0.8546 | 0.1610 | 0.3341 | 0.3542 |
| 168 | 0.4230 | 1.1230 | 1.0748 | 0.1790 | 0.3604 | 0.3434 |
| 169 | -1.2547 | 0.5817 | 0.4708 | 0.0610 | 0.3827 | 0.3425 |
| 170 | 1.6828 | 0.9795 | 1.0745 | 0.4494 | 0.2224 | 0.2446 |
| 171 | 1.6742 | 0.7212 | 1.4896 | 0.4159 | 0.1604 | 0.3458 |
| 172 | 1.7420 | 0.5073 | 1.2730 | 0.4781 | 0.1391 | 0.2991 |
| 173 | 0.2889 | 0.7989 | 0.6780 | 0.2045 | 0.3406 | 0.3018 |
| 174 | 0.7693 | 0.4656 | 0.6906 | 0.3199 | 0.2361 | 0.2957 |
| 175 | 1.0476 | 0.7422 | 0.9107 | 0.3379 | 0.2490 | 0.2946 |
| 176 | 1.8896 | 0.6019 | 0.9796 | 0.5466 | 0.1508 | 0.2200 |
| 177 | 0.3495 | 0.2845 | 1.2874 | 0.1924 | 0.1803 | 0.4916 |
| 178 | 0.7690 | 1.0672 | 1.0344 | 0.2430 | 0.3275 | 0.3169 |
| 179 | 1.0604 | 0.8088 | 0.8895 | 0.3371 | 0.2621 | 0.2841 |
| 180 | 2.9155 | 0.9914 | 1.1391 | 0.7302 | 0.1066 | 0.1236 |
| 181 | -1.1134 | 0.9013 | 0.4581 | 0.0611 | 0.4584 | 0.2943 |
The bottom-left graph in Chart 9 plots the relationship between the linear predictions of an initial and a final allowance for each of the impairments. In this case, the mean correlation is 0.56 (shown in Table 8). However, the corresponding probabilities in the bottom-right graph indicate the opposite effect (negative correlation). In other words, diagnoses that have a higher classification probability of an initial allowance tend to have a lower classification probability of a final allowance. The reason for the correlation inversion has to do with the fact that the probability of an outcome is a nonlinear function of the linear prediction of all the possible outcomes. As the linear prediction of an initial allowance dominates the magnitude of the other predictions, the classification probabilities of an initial denial not appealed, a final allowance, and a final denial can only decline.
The implications of high positive correlation between the linear predictions of an initial and a final allowance (bottom-left graph in Chart 9) can be further clarified with a somewhat extreme example involving the two impairments that are presented in Chart 10. The most common diagnosis in the musculoskeletal body system is a disorder of the back (discogenic and degenerative). The proportions in the entire sample of initial and final allowances for that impairment are about 23 percent and 38 percent, respectively. On the other hand, based on its effect on mortality alone, a highly disabling diagnosis is lung cancer (malignant neoplasm of the trachea, bronchus, or lung). In this case, 94 percent of the decisions result in an initial allowance, while only 3 percent of the outcomes represent a final allowance.
Lung cancer versus disorders of the back, by earnings: Linear predictions compared with probabilities
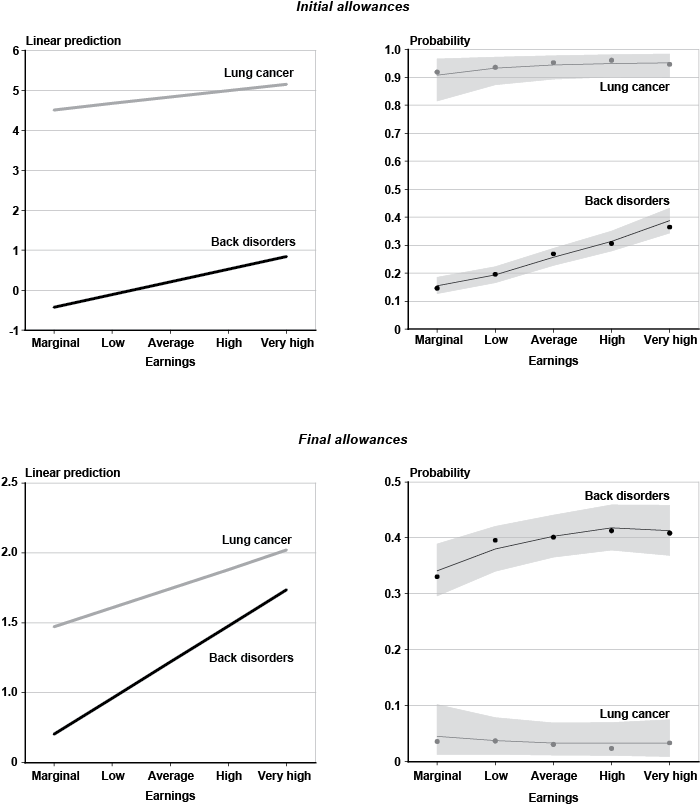
| Earnings | Linear prediction | Probability | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Disorders of the back | Lung cancer | |||||||||
| Disorders of the back | Lung cancer | Actual | 5th percentile | 50th percentile | 95th percentile | Actual | 5th percentile | 50th percentile | 95th percentile | |
| Initial allowances | ||||||||||
| Marginal | -0.4281 | 4.5062 | 0.1463 | 0.1266 | 0.1543 | 0.1848 | 0.9187 | 0.8163 | 0.9073 | 0.9656 |
| Low | -0.1087 | 4.6767 | 0.1962 | 0.1668 | 0.1939 | 0.2229 | 0.9356 | 0.8736 | 0.9325 | 0.9719 |
| Average | 0.2088 | 4.8333 | 0.2691 | 0.2273 | 0.2571 | 0.2882 | 0.9524 | 0.8941 | 0.9437 | 0.9765 |
| High | 0.5267 | 4.9950 | 0.3061 | 0.2791 | 0.3141 | 0.3504 | 0.9607 | 0.9017 | 0.9494 | 0.9800 |
| Very high | 0.8451 | 5.1514 | 0.3645 | 0.3443 | 0.3876 | 0.4317 | 0.9462 | 0.8999 | 0.9515 | 0.9832 |
| Final allowances | ||||||||||
| Marginal | 0.7033 | 1.4730 | 0.3307 | 0.2964 | 0.3414 | 0.3890 | 0.0362 | 0.0132 | 0.0455 | 0.1021 |
| Low | 0.9607 | 1.6072 | 0.3956 | 0.3408 | 0.3799 | 0.4205 | 0.0372 | 0.0130 | 0.0376 | 0.0784 |
| Average | 1.2195 | 1.7442 | 0.4011 | 0.3656 | 0.4027 | 0.4409 | 0.0309 | 0.0121 | 0.0337 | 0.0695 |
| High | 1.4780 | 1.8800 | 0.4130 | 0.3785 | 0.4180 | 0.4587 | 0.0238 | 0.0111 | 0.0331 | 0.0696 |
| Very high | 1.7368 | 2.0218 | 0.4085 | 0.3689 | 0.4128 | 0.4582 | 0.0336 | 0.0094 | 0.0332 | 0.0749 |
Suppose two claimants were identical in all measured characteristics (having the sample mean features), except one was diagnosed with lung cancer and the other had a back disorder. Linear predictions for those two claimants as a function of earnings appear on the left (top and bottom) graphs of Chart 10. Notice in particular how the predictions of an initial and a final allowance for the claimant with lung cancer exceed the predictions corresponding to the applicant with a back disorder. By contrast, the two graphs on the right side of the chart display point and interval probability predictions (90 percent posterior probability), which closely follow the observed sample proportions. For any outcome different from an initial allowance, the classification probabilities of lung cancer lie well below the probabilities of a disorder of the back. This, of course, is due to the extremely high probability of an initial allowance associated with a diagnosis of lung cancer in the first place.
In the two-impairment (lung cancer/back disorder) example, a significant fraction of claimants with back disorders are initially denied, but eventually allowed. Yet, claimants with lung cancer have a higher prediction of both an initial and a final allowance. Put differently, it is simply not the case that ALJs are favoring applicants with back disorders over those with lung cancer. Whether it is at the DDS or at the hearing level or above, lung cancer is determined to be a more disabling diagnosis than a back disorder. In general, the high positive correlation implies that in going from an initial to a final allowance, decision makers are largely preserving the ordinal ranking of impairments (a finding that is only evident when looking at the linear predictions and not the probabilities).
One might be tempted to conclude that this correlation finding provides evidence that decision makers are uniformly adhering to SSA's disability guidelines at the various adjudicative levels. However, other possible explanations cannot be ruled out. For example, Keiser (2010) hinted at evidence of a policy feedback mechanism, where knowledge of ALJ reversal rates affected the self-reported initial allowance rate of DDS examiners.18 If there was a feedback effect, it could also flow in either direction (from the DDS to the Office of Disability Adjudication and Review (ODAR) and vice versa), or from both directions simultaneously. The bottom line is that it is important not to overreach when it comes to interpreting my results. The positive correlation between the predictions of an initial and a final allowance could be potentially explained by a feedback effect, where decision makers at the two stages are influenced by each other's ranking of impairments. Nevertheless, whether a feedback mechanism or adherence to the guidelines explains the positive correlation, the result implies some degree of consistency.
Conclusion
This article explores the roles that primary diagnoses and state of origin play in explaining observed heterogeneity in disability outcomes by adjudicative stage. Disability determinations are separated into four mutually exclusive categories: (1) initial allowances, (2) initial denials not appealed, (3) final allowances, and (4) final denials. The main findings are as follows:
- The primary diagnosis codes carry greater predictive ability for placing claimants into adjudicative categories than all other explanatory variables that are entertained combined. Knowing the impairments of a sample of applicants yields more accurate classification probabilities than knowing their age, sex, state of origin, earnings, employment status in the year before filing, and application history combined.
- The prediction of an initial allowance (1) increases for males and higher earners, and (2) decreases for unemployed applicants and claimants who have applied before.
- The prediction of an initial denial not appealed (1) increases for males; and (2) decreases for higher earners, unemployed applicants, and claimants who have applied before.
- The prediction of a final allowance (1) increases for higher earners and claimants who have applied before, and (2) decreases for males and unemployed applicants.
- As a function of single year of age, the initial allowance rate has a u-shape defined at very young ages by small numbers of claimants with a predominance of mental impairments. A quadratic polynomial seems to reproduce the age profiles accurately.
- When claimants are grouped by state, variance decomposition suggests that most of the variation in outcomes is driven by individual-level heterogeneity within the states. On the other hand, almost half of the variation in initial allowances can be attributed to the various primary diagnoses. In some cases, the different mix of impairments in the population of claimants may explain a significant portion of the difference in initial allowances between two states. Still, a great deal of variation in outcomes remains unaccounted for by the models, particularly when it comes to identifying final denials.
- When applicants are grouped by diagnosis, there is high positive correlation between the predictions of an initial and a final allowance. To the best of my knowledge, that finding has never been documented in the literature. Impairments that are considered to be more disabling at the DDS level tend to also be considered more disabling at the hearing level or above. In other words, when moving from an initial to a final allowance, the severity ranking of the diagnoses is preserved to a good extent.
Appendix
| Body system and primary diagnosis | Initial | Final | Total | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| Infectious/parasitic diseases | 2,478 | 706 | 739 | 313 | 4,236 |
| Pulmonary tuberculosis | (X) | 13 | (X) | (X) | 27 |
| Symptomatic HIV | 1,559 | 298 | 283 | 98 | 2,238 |
| Asymptomatic HIV | 30 | 186 | 130 | 80 | 426 |
| Neurosyphilis | 19 | (X) | (X) | (X) | 36 |
| Mycobacterial, other chronic infections | 32 | 18 | (X) | (X) | 71 |
| Other infectious and parasitic disorders | 83 | 45 | 34 | 14 | 176 |
| Late effects of acute poliomyelitis | 568 | 50 | 115 | 31 | 764 |
| Neoplasms | 37,526 | 3,968 | 3,533 | 1,070 | 46,097 |
| Malignant neoplasm of tongue | 254 | 21 | 24 | 9 | 308 |
| Malignant neoplasm of salivary glands | (X) | (X) | (X) | (X) | 21 |
| Malignant neoplasm of esophagus | 1,123 | (X) | 36 | (X) | 1,179 |
| Malignant neoplasm of stomach | 641 | (X) | 24 | (X) | 687 |
| Malignant neoplasm of small intestine | 144 | (X) | 13 | (X) | 176 |
| Malignant neoplasm of colon or rectum | 3,528 | 514 | 435 | 126 | 4,603 |
| Malignant neoplasm of liver | 1,667 | 10 | 37 | (X) | 1,718 |
| Malignant neoplasm of gallbladder | 139 | (X) | (X) | (X) | 148 |
| Malignant neoplasm of pancreas | 1,357 | (X) | 24 | (X) | 1,394 |
| Malignant neoplasm of digestive system | 176 | (X) | (X) | (X) | 196 |
| Malignant neoplasm of trachea or lung | 8,249 | 161 | 281 | 50 | 8,741 |
| Malignant neoplasm of pleura | 332 | (X) | (X) | (X) | 347 |
| Malignant neoplasm of heart | (X) | (X) | (X) | (X) | 30 |
| Malignant neoplasm of bone and cartilage | 445 | (X) | 41 | (X) | 525 |
| Malignant neoplasm of connective tissue | 198 | 30 | (X) | (X) | 256 |
| Malignant melanoma of skin | 801 | (X) | 26 | (X) | 857 |
| Other malignant neoplasm of skin | 50 | 15 | (X) | (X) | 79 |
| Malignant neoplasm of breast | 4,717 | 1,370 | 731 | 345 | 7,163 |
| Kaposi's sarcoma | (X) | (X) | (X) | (X) | (X) |
| Malignant neoplasm of bladder | 451 | 65 | 57 | 12 | 585 |
| Malignant neoplasm of kidney | 977 | 64 | 63 | 23 | 1,127 |
| Malignant neoplasm of eye | (X) | (X) | (X) | (X) | 11 |
| Malignant neoplasm of brain | 2,507 | 55 | 111 | 21 | 2,694 |
| Malignant neoplasm of nervous system | (X) | (X) | (X) | (X) | 13 |
| Malignant neoplasm of thyroid gland | 87 | 38 | 33 | 13 | 171 |
| Malignant neoplasm of endocrine glands | 34 | (X) | (X) | (X) | 44 |
| Malignant neoplasm of other sites (head, neck) | 1,383 | 165 | 222 | 49 | 1,819 |
| Secondary malignant neoplasms | 232 | (X) | (X) | (X) | 244 |
| Malignant neoplasm of unspecified site | 47 | (X) | (X) | (X) | 58 |
| Lymphoma | 1,769 | 494 | 431 | 137 | 2,831 |
| Multiple myeloma | 900 | 45 | 123 | 12 | 1,080 |
| Leukemias | 1,626 | 89 | 128 | 25 | 1,868 |
| Benign neoplasm of brain | 430 | 159 | 208 | 73 | 870 |
| Neoplasm of uncertain behavior | (X) | (X) | (X) | (X) | 15 |
| Neoplasm of unspecified/unknown nature | (X) | (X) | (X) | (X) | (X) |
| Malignant neoplasm of genital organs | 3,191 | 520 | 395 | 123 | 4,229 |
| Endocrine, nutritional, and metabolic | 6,635 | 4,517 | 4,842 | 1,947 | 17,941 |
| All disorders of thyroid | 42 | 146 | 129 | 67 | 384 |
| Diabetes mellitus | 3,014 | 3,490 | 3,345 | 1,387 | 11,236 |
| All disorders of parathyroid gland | (X) | (X) | (X) | (X) | (X) |
| All disorders of pituitary gland | (X) | (X) | 15 | (X) | 28 |
| All disorders of adrenal glands | (X) | (X) | (X) | (X) | 22 |
| Malnutrition (weight loss) | 113 | (X) | 32 | (X) | 164 |
| Disorders of plasma protein metabolism | (X) | (X) | (X) | (X) | (X) |
| Gout | 65 | 75 | 75 | 37 | 252 |
| Disorders of metabolism (cystic fibrosis) | 85 | (X) | 11 | (X) | 112 |
| Obesity and other hyperalimentation | 3,229 | 725 | 1,140 | 416 | 5,510 |
| Disorders of the immune mechanism | 77 | 38 | 89 | 18 | 222 |
| Diseases of the blood | 623 | 173 | 175 | 79 | 1,050 |
| Deficiency anemias | 48 | 23 | 26 | 14 | 111 |
| Hereditary hemolytic anemias | 143 | 35 | 27 | 12 | 217 |
| Aplastic anemia | 152 | (X) | 21 | (X) | 184 |
| Other anemias | 148 | 53 | 39 | 15 | 255 |
| Coagulation defects | (X) | (X) | (X) | (X) | 28 |
| Purpura and other hemorrhagic conditions | 14 | 14 | (X) | (X) | 47 |
| Other diseases of blood-forming organs | 109 | 36 | 40 | 23 | 208 |
| Mental disorders | 41,770 | 13,117 | 17,007 | 5,641 | 77,535 |
| Organic mental disorders | 8,024 | 740 | 1,878 | 308 | 10,950 |
| Schizophrenic, paranoid, psychotic disorders | 3,963 | 650 | 665 | 186 | 5,464 |
| Affective/mood disorders | 19,678 | 8,466 | 11,290 | 3,768 | 43,202 |
| Autistic disorders | 75 | (X) | (X) | (X) | 89 |
| Anxiety disorders | 3,817 | 1,477 | 2,096 | 736 | 8,126 |
| Personality disorders | 457 | 280 | 177 | 119 | 1,033 |
| Substance addiction (alcohol) | (X) | 439 | (X) | 186 | 777 |
| Substance addiction (drugs) | (X) | 218 | (X) | 64 | 342 |
| Somatoform disorders | 216 | 61 | 162 | 32 | 471 |
| Eating and tic disorders | (X) | (X) | (X) | (X) | (X) |
| Attention deficit disorder | 44 | 32 | 11 | 19 | 106 |
| Learning disorder | 54 | 103 | 17 | 21 | 195 |
| Mental retardation | 5,079 | 335 | 311 | 81 | 5,806 |
| Borderline intellectual functioning | 354 | 310 | 184 | 119 | 967 |
| Nervous system and sense organs | 20,239 | 6,891 | 8,773 | 3,313 | 39,216 |
| Cerebral degenerations | 36 | (X) | (X) | (X) | 48 |
| Brain atrophy | 713 | 97 | 163 | 37 | 1,010 |
| Parkinson's disease | 1,315 | 137 | 300 | 50 | 1,802 |
| Anterior horn cell disease | 690 | (X) | (X) | (X) | 740 |
| Other diseases of spinal cord | 763 | 43 | 110 | 18 | 934 |
| Disorders of autonomous nervous system | 155 | 67 | 107 | 33 | 362 |
| Multiple sclerosis | 3,543 | 588 | 1,612 | 311 | 6,054 |
| Cerebral palsy | 549 | 68 | 70 | 29 | 716 |
| Epilepsy | 727 | 1,290 | 901 | 592 | 3,510 |
| Migraine | 349 | 446 | 488 | 217 | 1,500 |
| Other neurological conditions | 1,365 | 888 | 1,135 | 485 | 3,873 |
| Carpal tunnel syndrome | 117 | 174 | 213 | 103 | 607 |
| Diabetic and other peripheral neuropathy | 2,478 | 554 | 1,186 | 292 | 4,510 |
| Myoneural disorders | 430 | 260 | 376 | 159 | 1,225 |
| Muscular dystrophies | 532 | 65 | 162 | 44 | 803 |
| Retinal detachments and defects | 207 | 103 | 78 | 42 | 430 |
| Other retina disorders | 644 | 151 | 212 | 51 | 1,058 |
| Glaucoma | 200 | 126 | 94 | 65 | 485 |
| Cataract | 61 | 99 | 44 | 26 | 230 |
| Visual disturbances | 437 | 400 | 326 | 148 | 1,311 |
| Blindness and low vision | 2,838 | 554 | 552 | 226 | 4,170 |
| Cardiac transplantation | 62 | (X) | (X) | (X) | 75 |
| Disorders of eye movements | (X) | (X) | (X) | (X) | 13 |
| Disorders of vestibular system | 284 | 194 | 299 | 122 | 899 |
| Other disorders of ear | 38 | 127 | 58 | 54 | 277 |
| Deafness | 1,704 | 439 | 229 | 202 | 2,574 |
| Circulatory | 28,256 | 9,336 | 12,593 | 3,852 | 54,037 |
| Rheumatic fever with heart involvement | (X) | (X) | (X) | (X) | (X) |
| Diseases of aortic valve | 297 | 192 | 221 | 84 | 794 |
| Other rheumatic heart disease | 70 | (X) | 25 | (X) | 124 |
| Essential hypertension | 412 | 1,706 | 1,192 | 696 | 4,006 |
| Hypertensive vascular disease | 538 | 467 | 453 | 172 | 1,630 |
| Hypertensive vascular and renal disease | 14 | (X) | (X) | (X) | 30 |
| Acute myocardial infarction | 566 | 435 | 385 | 119 | 1,505 |
| Angina without ischemic heart disease | 126 | 106 | 113 | 37 | 382 |
| Chronic ischemic heart disease | 7,977 | 3,132 | 5,107 | 1,395 | 17,611 |
| Chronic pulmonary heart disease | 378 | 42 | 68 | 14 | 502 |
| Valvular heart disease/other defects | 229 | 169 | 217 | 81 | 696 |
| Cardiomyopathy | 2,514 | 554 | 1,016 | 264 | 4,348 |
| Cardiac dysrhythmias | 412 | 282 | 363 | 141 | 1,198 |
| Heart failure | 2,972 | 480 | 737 | 153 | 4,342 |
| Late effects of cerebrovascular disease | 7,786 | 984 | 1,478 | 371 | 10,619 |
| Aortic aneurysm | 201 | 72 | 100 | 26 | 399 |
| Peripheral vascular (arterial) disease | 2,373 | 254 | 550 | 96 | 3,273 |
| Periarteritis nodosa, allied conditions | 50 | (X) | (X) | (X) | 71 |
| Disease of capillaries | (X) | (X) | (X) | (X) | (X) |
| Phlebitis and thrombophlebitis | 106 | 72 | 79 | 38 | 295 |
| Varicose veins of lower extremities | 292 | 70 | 80 | 29 | 471 |
| Other diseases of circulatory system | 942 | 280 | 381 | 123 | 1,726 |
| Respiratory | 11,539 | 2,671 | 3,528 | 1,313 | 19,051 |
| Chronic bronchitis | 41 | 53 | 60 | 29 | 183 |
| Emphysema | 890 | 150 | 195 | 52 | 1,287 |
| Asthma | 786 | 1,148 | 996 | 564 | 3,494 |
| Bronchiectasis | 33 | 15 | (X) | (X) | 66 |
| Chronic pulmonary insufficiency | 9,271 | 1,014 | 1,898 | 509 | 12,692 |
| Asbestosis | 43 | (X) | 39 | (X) | 106 |
| Pneumoconiosis | (X) | (X) | 10 | (X) | 20 |
| Other diseases of the respiratory system | 471 | 270 | 318 | 144 | 1,203 |
| Digestive | 3,918 | 2,322 | 2,772 | 1,049 | 10,061 |
| Diseases of esophagus | 17 | 22 | 20 | 13 | 72 |
| Peptic ulcer (gastric or duodenal) | 28 | 41 | 21 | 15 | 105 |
| Gastritis and duodenitis | (X) | 48 | 44 | (X) | 128 |
| Hernias | 72 | 160 | 176 | 73 | 481 |
| Crohn's disease | 297 | 266 | 423 | 137 | 1,123 |
| Idiopathic proctocolitis | 89 | 94 | 114 | 51 | 348 |
| Other diseases of gastrointestinal system | 397 | 694 | 729 | 291 | 2,111 |
| Chronic liver disease, cirrhosis | 2,968 | 970 | 1,224 | 439 | 5,601 |
| Gastrointestinal hemorrhage | 41 | 27 | (X) | (X) | 92 |
| Genitourinary | 6,043 | 500 | 686 | 176 | 7,405 |
| Nephrotic syndrome | 219 | 56 | 79 | 23 | 377 |
| Chronic renal failure | 5,731 | 144 | 376 | 36 | 6,287 |
| Other diseases of the urinary tract | 81 | 175 | 183 | 81 | 520 |
| Disorders of the genital organs | 12 | 125 | 48 | 36 | 221 |
| Skin | 255 | 308 | 285 | 122 | 970 |
| Bullous disease | (X) | (X) | (X) | (X) | 13 |
| Ichthyosis | 32 | 56 | 73 | 22 | 183 |
| Dermatitis/psoriasis | 80 | 99 | 77 | 26 | 282 |
| Other disorders of the skin | 138 | 149 | 133 | 72 | 492 |
| Musculoskeletal | 46,164 | 36,793 | 53,485 | 21,329 | 157,771 |
| Diffuse diseases of connective tissue | 1,075 | 483 | 919 | 295 | 2,772 |
| Rheumatoid arthritis | 4,138 | 1,093 | 1,904 | 504 | 7,639 |
| Osteoarthrosis and allied disorders | 14,398 | 6,341 | 8,852 | 3,208 | 32,799 |
| Other and unspecified arthropathies | 810 | 683 | 705 | 304 | 2,502 |
| Ankylosing spondylitis | 308 | 134 | 222 | 65 | 729 |
| Disorders of back (discogenic and degenerative) | 19,797 | 21,150 | 33,682 | 13,237 | 87,866 |
| Disorders of muscle, ligament, and fascia | 3,484 | 5,518 | 5,696 | 3,072 | 17,770 |
| Osteomyelitis and other bone infection | 258 | 86 | 99 | 30 | 473 |
| Other disorders of bone and cartilage | 1,761 | 1,165 | 1,265 | 518 | 4,709 |
| Curvature of spine | 135 | 140 | 141 | 96 | 512 |
| Congenital | 123 | 59 | 62 | 33 | 277 |
| Spina bifida | 44 | (X) | (X) | (X) | 60 |
| Congenital anomalies of heart | 60 | 40 | 31 | 19 | 150 |
| Other congenital anomalies | 19 | (X) | 25 | (X) | 67 |
| Injuries | 8,282 | 8,435 | 6,632 | 3,582 | 26,931 |
| Multiple body dysfunctions | (X) | (X) | (X) | (X) | 14 |
| Sleep-related breathing disorders | 85 | 107 | 150 | 74 | 416 |
| Loss of voice | 109 | 21 | 28 | 18 | 176 |
| Fracture of vertebral column | 912 | 108 | 117 | 29 | 1,166 |
| Fracture of upper limb | 597 | 1,069 | 692 | 398 | 2,756 |
| Fracture of lower limb | 2,178 | 2,309 | 1,836 | 835 | 7,158 |
| Other fractures of bones | 340 | 546 | 425 | 218 | 1,529 |
| Dislocations (all types) | 104 | 206 | 135 | 63 | 508 |
| Sprains and strains (all types) | 436 | 2,222 | 1,407 | 1,125 | 5,190 |
| Intracranial injury | 593 | 213 | 195 | 72 | 1,073 |
| Internal injury | 10 | (X) | 17 | (X) | 41 |
| Open wound, except limbs | (X) | (X) | (X) | (X) | (X) |
| Open wound upper limb (soft tissue) | 216 | 303 | 206 | 117 | 842 |
| Open wound lower limb (soft tissue) | 211 | 177 | 146 | 72 | 606 |
| Amputations | 1,292 | 770 | 718 | 350 | 3,130 |
| Late effects of injuries to nervous system | 1,039 | 225 | 301 | 119 | 1,684 |
| Chronic fatigue syndrome | 102 | 92 | 211 | 67 | 472 |
| Burns (code 9480) | 32 | 33 | 26 | 11 | 102 |
| Burns (code 9490) | 19 | 22 | (X) | (X) | 62 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | |||||
| NOTE: (X) = suppressed to avoid disclosing information about particular individuals. | |||||
| State | Initial | Final | Total | ||
|---|---|---|---|---|---|
| Allowances | Denials not appealed | Allowances | Denials | ||
| Alabama | 3,858 | 1,583 | 3,620 | 625 | 9,686 |
| Alaska | 286 | 145 | 85 | 36 | 552 |
| Arizona | 4,707 | 1,492 | 1,725 | 588 | 8,512 |
| Arkansas | 2,589 | 913 | 1,853 | 533 | 5,888 |
| California | 23,358 | 10,492 | 8,279 | 4,456 | 46,585 |
| Colorado | 2,106 | 1,368 | 1,495 | 507 | 5,476 |
| Connecticut | 2,820 | 934 | 1,137 | 479 | 5,370 |
| Delaware | 828 | 239 | 254 | 115 | 1,436 |
| Florida | 11,372 | 5,180 | 8,082 | 2,839 | 27,473 |
| Georgia | 5,084 | 2,808 | 4,310 | 1,428 | 13,630 |
| Hawaii | 872 | 286 | 142 | 96 | 1,396 |
| Idaho | 918 | 377 | 421 | 174 | 1,890 |
| Illinois | 8,179 | 3,411 | 3,794 | 1,416 | 16,800 |
| Indiana | 4,822 | 2,555 | 3,112 | 1,420 | 11,909 |
| Iowa | 2,339 | 752 | 690 | 386 | 4,167 |
| Kansas | 1,817 | 814 | 804 | 371 | 3,806 |
| Kentucky | 3,552 | 1,355 | 3,291 | 1,119 | 9,317 |
| Louisiana | 2,934 | 1,388 | 1,956 | 709 | 6,987 |
| Maine | 1,313 | 366 | 678 | 183 | 2,540 |
| Maryland | 2,908 | 1,281 | 1,500 | 467 | 6,156 |
| Massachusetts | 5,163 | 1,280 | 1,955 | 646 | 9,044 |
| Michigan | 9,584 | 4,858 | 5,087 | 1,888 | 21,417 |
| Minnesota | 4,209 | 1,311 | 1,539 | 625 | 7,684 |
| Mississippi | 2,343 | 1,112 | 1,683 | 738 | 5,876 |
| Missouri | 5,336 | 1,846 | 2,499 | 846 | 10,527 |
| Montana | 537 | 291 | 353 | 177 | 1,358 |
| Nebraska | 1,261 | 514 | 382 | 221 | 2,378 |
| Nevada | 1,688 | 529 | 455 | 195 | 2,867 |
| New Hampshire | 1,377 | 320 | 406 | 106 | 2,209 |
| New Jersey | 6,863 | 1,964 | 2,549 | 856 | 12,232 |
| New Mexico | 1,285 | 530 | 584 | 238 | 2,637 |
| New York | 15,947 | 6,143 | 8,596 | 2,667 | 33,353 |
| North Carolina | 7,277 | 3,367 | 5,064 | 1,665 | 17,373 |
| North Dakota | 328 | 150 | 170 | 81 | 729 |
| Ohio | 8,028 | 3,871 | 4,658 | 2,150 | 18,707 |
| Oklahoma | 2,834 | 1,518 | 2,068 | 859 | 7,279 |
| Oregon | 2,939 | 1,278 | 1,226 | 644 | 6,087 |
| Pennsylvania | 11,635 | 4,056 | 4,866 | 2,050 | 22,607 |
| Rhode Island | 1,190 | 282 | 502 | 209 | 2,183 |
| South Carolina | 3,769 | 1,588 | 2,925 | 896 | 9,178 |
| South Dakota | 468 | 199 | 158 | 116 | 941 |
| Tennessee | 4,030 | 1,851 | 4,182 | 1,154 | 11,217 |
| Texas | 10,728 | 5,751 | 6,669 | 3,135 | 26,283 |
| Utah | 1,000 | 486 | 628 | 289 | 2,403 |
| Vermont | 490 | 171 | 188 | 72 | 921 |
| Virginia | 5,478 | 2,096 | 2,832 | 1,117 | 11,523 |
| Washington | 4,638 | 2,048 | 1,816 | 786 | 9,288 |
| West Virginia | 2,004 | 778 | 2,009 | 567 | 5,358 |
| Wisconsin | 4,478 | 1,700 | 1,664 | 775 | 8,617 |
| Wyoming | 282 | 169 | 171 | 104 | 726 |
| SOURCE: Author's calculations based on a 10 percent random sample of the DRF. | |||||
Notes
1 According to the Social Security Advisory Board (2012a), CDRs over the 1996–2008 period resulted on average in more than $10 of savings per $1 spent. Yet, because of budgetary constraints, the number of processed CDRs declined from its peak of more than 1.8 million in 2000 to about 1.1 million by 2009.
2 In 10 states, a Prototype process initiated in 1999 allows claimants receiving an initial denial to appeal directly to the hearing level without having to go through the reconsideration stage.
3 The figures in Table 1 are derived from SSA (2009, Tables 60, 61, and 62). Additional years of data appear in those tables. The reason why concurrent applicants are excluded is discussed in the data and methodology section of this article.
4 The ability to test the impact of any of these factors on the reversal rate of initial denials falls outside the scope of this investigation because of the lack of readily available data. The focus here is on the capacity of primary diagnosis codes to successfully predict disability outcomes through the adjudicative process. A recent preliminary publication by the Social Security Advisory Board (2012b) suggested that third-party representation at the initial determination level increases the likelihood of an allowance substantially for SSI claimants, but only marginally for DI applicants.
5 For a summary on litigation affecting the disability determination process, see the Social Security Advisory Board (2012a).
6 Rupp's model did not use the individual primary diagnosis codes, but instead used 16 body systems, which group the specific impairments (15 dummy variables in addition to the musculoskeletal body group serving as the reference category).
7 Technical denials can occur for a variety of nonmedical reasons, such as engaging in SGA or lacking the required amount of work credits.
8 For estimation purposes, a 10 percent random sample is used instead of the full DRF because of the computational demands of the estimated models. The 100 percent figures reported in Table 2 are directly derived from the values in Table 1. There are small discrepancies between the two sets of figures. For instance, the 10 percent random sample culls any observations without a known primary diagnosis code or outside the 50 states (Puerto Rico, the District of Columbia, and other territories).
9 Notice that when estimated from a classical perspective, random coefficient models like the ones in this article make distributional assumptions about subsets of parameters that are in effect no different from those of a prior density. In other words, classical statisticians may also use prior distributions, even if they do not refer to them as such.
10 All of the models are estimated using Markov Chain Monte Carlo (MCMC) methods. The algorithm is an example of what is known as a Metropolis-within-Gibbs random sampler. A "noninformative" proper prior specification is adopted, with hyperparameter values as suggested by Rossi, Allenby, and McCulloch (2005).
11 In this article, I focus exclusively on the primary diagnosis codes. A cross-classification of unique primary and secondary diagnosis code combinations would yield many thousands of clusters nesting the individual-level data. Forthcoming research by the author investigates the correlation patterns between primary and secondary diagnosis codes among initial determinations.
12 To the best of my knowledge, the full extent to which the primary diagnosis change may occur on appeal across the full listing of impairments has never been documented.
13 Because sex is an individual-level predictor in my models, I merge a few primary impairments that are gender specific. The single category "malignant neoplasm of the genital organs" combines four female diagnosis codes (malignant neoplasms of the uterus, cervix, ovaries, and other female genital organs) with three male diagnosis codes (malignant neoplasms of the prostate, testes, and penis and other male genital organs).
14 In a Bayesian context, the mean and standard deviation of the posterior density can be used to compute approximate bounds on the posterior probability that a parameter changes sign (much like the t-statistics typically reported in the classical approach).
15 If a model includes claimant-level predictors, there is a group variance parameter estimate associated with every explanatory variable and not just with the intercepts. However, because the claimant-level predictors have been centered around their grand mean, the intercepts carry the interpretation of adjusted mean linear predictions (see Raudenbush and Bryk (2002)).
16 In discrete categorical models, a common identification restriction imposes a constant variance. For the multinomial logit case, the within-group variance has a logistic distribution with variance π²/3. I follow the approach in Grilli and Rampichini (2007) to recover the ICC estimates.
17 Notice that a fixed-effects model with the primary impairments rather than body systems would have required 180 indicator variables in the regression, potentially posing serious computational difficulties. In addition, it is unlikely that using the impairments would have substantially increased the share of explained state-level variation.
18 Surprisingly, as many as 77 percent of the survey respondents were unaware of any activities at the hearing level or above, which appears to undercut the relevance of the result.
References
Coe, Norma B., Kelly Haverstick, Alicia H. Munnell, and Anthony Webb. 2011. "What Explains State Variation in SSDI Application Rates?" CRR Working Paper No. 2011-23. Chestnut Hill, MA: Center for Retirement Research at Boston College.
Congdon, Peter. 2005. Bayesian Models for Categorical Data. New York, NY: John Wiley & Sons.
Congressional Budget Office. 2010. "Social Security Disability Insurance: Participation Trends and Their Fiscal Implications." Economic and Budget Issue Brief. Washington, DC: Congressional Budget Office, Health and Human Resources Division (July 22).
Grilli, Leonardo, and Carla Rampichini. 2007. "A Multilevel Multinomial Logit Model for the Analysis of Graduates' Skills." Statistical Methods & Applications 16: 381–393.
Hu, Jianting, Kajal Lahiri, Denton R. Vaughan, and Bernard Wixon. 2001. "A Structural Model of Social Security's Disability Determination Process." Review of Economics and Statistics 83(2): 348–361.
Keiser, Lael R. 2010. "Understanding Street-Level Bureaucrats' Decision Making: Determining Eligibility in the Social Security Disability Program." Public Administration Review 72(2): 247–257.
Lahiri, Kajal, Denton R. Vaughan, and Bernard Wixon. 1995. "Modeling SSA's Sequential Disability Determination Process Using Matched SIPP Data." Social Security Bulletin 58(4): 3–42.
Leonesio, Michael V., Denton R. Vaughan, and Bernard Wixon. 2003. "Increasing the Early Retirement Age Under Social Security: Health, Work and Financial Resources." Health and Income Security for an Aging Workforce, Brief No. 7. Washington, DC: National Academy of Social Insurance.
Panis, Constantijn, Ronald Euller, Cynthia Grant, Melissa Bradley, Christin E. Peterson, Randall Hirscher, and Paul Steinberg. 2000. SSA Program Data User's Manual. Prepared by the RAND Corporation (contract no. PM-973-SSA) for the Social Security Administration.
Raudenbush, Stephen W., and Anthony S. Bryk. 2002. Hierarchical Linear Models: Applications and Data Analysis Methods, 2nd edition. Thousand Oaks, CA: Sage Publications, Inc.
Rossi, Peter E., Greg M. Allenby, and Rob McCulloch. 2005. Bayesian Statistics and Marketing. New York, NY: John Wiley & Sons.
Rupp, Kalman. 2012. "Factors Affecting Initial Disability Allowance Rates for the Disability Insurance and Supplemental Security Income Programs: The Role of the Demographic and Diagnostic Composition of Applicants and Local Labor Market Conditions." Social Security Bulletin 72(4): 11–35.
Rupp, Kalman, and David Stapleton. 1995. "Determinants of the Growth in the Social Security Administration's Disability Programs: An Overview." Social Security Bulletin 58(4): 43–70.
Social Security Administration. 2009. Annual Statistical Report on the Social Security Disability Insurance Program, 2008. Washington, DC: Office of Retirement and Disability Policy, Office of Research, Evaluation, and Statistics.
———, Office of the Inspector General. 2010. Disability Impairments on Cases Most Frequently Denied by Disability Determination Services and Subsequently Allowed by Administrative Law Judges. Audit Report No. A-07-09-19083. Baltimore, MD: Office of the Inspector General.
Social Security Advisory Board. 2001. Charting the Future of Social Security's Disability Programs: The Need for Fundamental Change. Washington, DC: Social Security Advisory Board (January).
———. 2006. Disability Decision Making: Data and Materials. Washington, DC: Social Security Advisory Board (May).
———.2012a. Aspects of Disability Decision Making: Data and Materials. Washington, DC: Social Security Advisory Board (February).
———. 2012b. Filing for Social Security Disability Benefits: What Impact Does Professional Representation Have on the Process at the Initial Application Level? Washington, DC: Social Security Advisory Board (September).
Spiegelhalter, David J., Nicola G. Best, Bradley P. Carlin, and Angelika van der Linde. 2002. "Bayesian Measures of Model Complexity and Fit (with discussion)." Journal of the Royal Statistical Society (Series B) 64(4): 583–639.
SSA. See Social Security Administration.
Strand, Alexander. 2002. "Social Security Disability Programs: Assessing the Variation in Allowance Rates." ORES Working Paper Series No. 98. Washington, DC: Social Security Administration, Office of Research, Evaluation, and Statistics (August).