The Out-of-Sample Performance of Stochastic Methods in Forecasting Age-Specific Mortality Rates
ORES Working Paper No. 111 (released July 2008)
This paper evaluates the out-of-sample performance of two stochastic models used to forecast age-specific mortality rates: (1) the model proposed by Lee and Carter (1992); and (2) a set of univariate autoregressions linked together by a common residual covariance matrix (Denton, Feavor, and Spencer 2005). To this aim, death rates from 16 industrialized nations are used to compare observed ex-post mortality rates to the forecasts generated by the models. Several functions of the individual age-specific mortality rates are also entertained, including life expectancy at birth (e0), as well as alternative measures of the age-dependency ratio. The latter are constructed based on how the individual mortality rates enter a population projection, and thus, are meant to gauge the potential impact of mortality alone on public retirement programs. In general, both models are found to produce point forecasts for the individual mortality rates, life expectancy, and the dependency ratios that are fairly close to one another. Typically, the median projections of mortality moderately overpredict the actual death rates, particularly for the oldest age groups (ages 65–95 or older). Conversely, the large majority of the point forecasts of life expectancy at birth and the dependency ratios underestimate their observed values. The models also generate interval forecasts of e0 that are "too wide" as their empirical probability content often exceeds their nominal coverage. However, the Lee-Carter model tends to seriously underpredict the forecast uncertainty associated with both the death rates of the oldest ages and the age-dependency ratios, while the autoregressive approach overpredicts this uncertainty in most cases.
The author is with the Division of Economic Research, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Working papers in this series are preliminary materials circulated for review and comment. The findings and conclusions expressed in them are the authors' and do not necessarily represent the views of the Social Security Administration.
Introduction
Mortality is one of the key demographic variables affecting the flow of income and expenditures in pay-as-you-go public retirement programs. Indeed, a combination of population aging and declining fertility rates largely drives the currently projected financial imbalance in the U.S. Social Security system. In recent years, official mortality forecasts in a number of industrialized nations have come under greater scrutiny. The deterministic nature of these projections and the role that expert judgment plays in shaping them are often viewed by academics as sources of contention. Meanwhile, demographers and other social scientists are increasingly turning to statistical time series techniques to generate mortality forecasts that are consistent with a probabilistic representation of uncertainty.
This paper will evaluate the performance of two alternative stochastic approaches that can be applied to project age-specific mortality rates. Mortality data from 16 industrialized nations is used to carry out an extensive out-of-sample validation exercise comparing actual mortality rates to the pseudo-forecasts generated by the models. This analysis differs from other ex-post assessments published in the literature in two respects: First, in addition to reporting several single-valued aggregate measures of performance, it also investigates how forecast error is distributed across age groups and forecast horizons. Second, this paper is not only concerned with a model's ability to produce accurate point projections, but also with its capacity to generate a realistic depiction of forecast uncertainty in terms of the empirical probability content of its interval forecasts.
The remainder of the paper is structured as follows: an introduction of the two models that are the focus of the investigation; a description of the experimental design, followed by the proposed ex-post validation exercise, and a discussion on the most salient features of the mortality data used in the paper; a presentation on the out-of-sample performance results; and the conclusion.
The Models
Stochastic forecasts are typically generated based on some underlying time-series statistical model. This time series approach often involves a specified random disturbance shock process, as well as a recursive expression that posits current values of the series in question as a function of previous values. Once the model is fit to a particular data set and estimates of its parameters obtained, future values of the series can be produced by iterating the model forward. For simple models, the forecast distribution may be available in closed-form. Otherwise, the researcher can turn to simulation by drawing from the disturbance process to generate random sample paths of forthcoming observations. In either case, the result is not only a single point forecast but an entire probability distribution describing the uncertainty associated with future outcomes.
Modeling and projecting age-specific mortality rates over time is a high-dimensional forecasting problem. Following the taxonomy suggested in Bell (1997), stochastic projection models can be categorized as parametric or nonparametric, although this can be a somewhat artificial distinction. The parametric or curve-fitting approach involves fitting a curve defined by a finite set of time-varying parameters to the mortality data, based on some optimization criterion. The resulting parameter estimates are then treated as a time series that is projected to recover the different paths of the curve into the future (that is, the mortality forecasts). The nonparametric approach relies on principal components analysis to yield a linear transformation of the data, often in terms of an approximation of reduced dimensions (one or a few principal components).
Stochastic projection methods can be further classified as univariate or multivariate depending on whether the generated forecasts take into account the interdependencies across the age groups. The former proceed by individually fitting each age-specific mortality rate to a univariate time series equation. Although the forecasts produced by univariate methods ignore the typically high cross-correlation among the different age series, they do not necessarily perform worse than multivariate models. For instance, in an ex-post validation experiment, Bell (1997) found that a random-walk with drift applied to each age series led to better short-term forecast performance than any of a variety of multivariate approaches. Nonetheless, there are several problems associated with the univariate route. First, while the projections may be more accurate for each individual age group, they can jointly imply unreasonable behavior. In particular, univariate methods can lead to odd shapes in the fairly regular structure of mortality over the entire age profile. Similarly, since this approach ignores the high degree of correlation among the age series, it is unlikely to provide an accurate picture of overall forecast uncertainty.
This paper focuses on the forecast performance of two models. First, the multivariate nonparametric method proposed by Lee and Carter (1992). This model has gained increasing recognition over the years, becoming a benchmark technique to the most recent technical advisory panels to the Social Security Administration, the U.S. Census Bureau, and several agencies around the world. The second model involves one of the approaches suggested by Denton, Feaver, and Spencer (2005). This parametric model fits first-order autoregressive processes to each age group separately. The resulting residuals are then used to estimate the covariance matrix of the multivariate disturbance process driving joint future variation in the age-specific mortality rates.
The Lee-Carter Model
The approach to mortality modeling proposed by Lee and Carter (1992) postulates the logarithm of a set of age-specific mortality rates as the sum of a time-invariant age-specific element and a second component that changes over time. Formally, let M represent the A × T dimensional matrix of mortality rates with individual elements denoting the death rate for the population of individuals at age a and time t. Then,
for a = 1,…A, and t = 1,…T.
The age-specific set of parameters αa describes the average shape of the log-mortality rates for every age category. The second component is the product of a time-varying index or trend of the general level of mortality kt and a set of coefficients βa that determine both the direction and magnitude by which mortality at every age varies with the index. Notice also that the parameters βa and kt are not uniquely identified, since for any given constant c, an equivalent representation results by using and . Thus, Lee and Carter (1992) suggest imposing the following constraints:
These constraints imply that the estimate of αa is simply the sample mean of the log-mortality rates.
The Lee-Carter model represents a special case of the principal components (PC) analysis applied by Bell and Monsell (1991) to forecast age-specific mortality rates. Intuitively, PC analysis yields an approximation of the A age-specific mortality rates as the linear combination of p "basic elements" or principal components estimated from the data, where typically p ≤ A. One way to compute the latter is via singular value decomposition (SVD). Specifically, let M define the matrix of centered age profiles obtained by subtracting the A sample logarithmic mortality means from the columns of the matrix log(M). The singular value decomposition of M yields a representation involving the product of the following three matrices:
where L is a diagonal matrix with the singular values ordered from high to low, while B is an orthonormal matrix whose first p columns correspond to the first p principal components.1 The Lee-Carter model uses only the first principal component (p = 1). Therefore, the easiest way to estimate its parameters is by setting to the sample mean of the log-mortality rates, to the first column of B, and to the first row of LU′ subject to the constraints in (2). These parameter values can be thought of as the least square estimates resulting from minimizing the sum of squared errors function
Once equation (1) is fitted to the data, the parameter estimates and are taken to be fixed, while the log mortality index provides a univariate time series whose future values can be forecasted using standard Box-Jenkins techniques. In most applications, a random-walk with drift is empirically found to yield a suitable fit to
leading to the following maximum likelihood estimates for the drift and variance parameters:2
Moreover, future values of can be obtained either analytically or via simulation, by iterating equation (5) forward
where conditionally on the estimates , ,…, , the usual mean forecast is a straight line as a function of the forecast horizon h with slope
It is then a simple matter to "plug" the projected values of the log-mortality index back into equation (1) to recover the forecasts associated with each age-specific future mortality
The Lee-Carter model yields a parsimonious stochastic approach to mortality forecasting that is easy to implement and often produces reasonable forecasts for all-cause age-specific mortality. The method, however, is not without its limitations. First, a linear trend in the mortality index kt does not hold empirically in very long data sets. It entails a constant geometric rate of decline for each age-specific mortality
Yet, there is evidence that in a number of industrialized countries, the age pattern of mortality decline over the past few decades has reversed (Lee and Miller; 2001). In particular, the rapid decline in infant and child mortality characterizing the first half of the twentieth century has diminished, with mortality decreasing faster for the elderly. Furthermore, the Lee-Carter model implies that the rates of mortality decline for different ages (for instance, a1 and a2) maintain a constant ratio to each other over time, regardless of which univariate time series process is used to forecast kt :
As a result, the assumption of holding βa constant over time seems unrealistic.
Finally, the Lee-Carter model incorporates uncertainty through a single source (the sampling uncertainty derived from forecasting kt). It is also possible to accommodate additional uncertainty about the trend in mortality linked to the estimate of the drift parameter μ, as Lee and Carter (1992) originally discussed. However, this still ignores uncertainty in the estimation of the βa coefficients associated with kt as well as the error from fitting the model using only the first principal component. Some demographers have criticized the model's interval forecasts as implausibly narrow.
Some Extensions of the Lee-Carter Model
There have been a number of refinements to the Lee-Carter specification. In fact, in their original article, Lee and Carter (1992) addressed the two modifications considered in this paper. In particular, the authors observed that the models' forecasts do not match the initial conditions in the jump-off year (that is, the forecasts are not linked to the actual mortality rates at the end of the base period). One easy way to solve this problem is to set αa equal to the most recently observed logarithmic age-specific rates, instead of their time average. However, Lee and Carter (1992) caution that such an approach might extrapolate features of mortality that are specific to the jump-off year and could have a negative impact on model fit and forecast performance. In subsequent papers, Lee (2000) and Lee and Miller (2002) seem to have reconsidered this position, favoring the modified value of αa for forecasting purposes. Bell (1997), who also supports this bias correction step, finds dramatic improvements in short-term out-of-sample forecast performance when setting αa equal to the logarithm of the age-specific rates in the base year.3
Another improvement to the Lee-Carter model is concerned with the fact that the OLS estimates of its parameters are the values minimizing error in the logarithm of the death rates, rather than the death rates themselves. Consequently, the total number of deaths predicted by the model is not guaranteed to match the observed death counts in the sample. Lee and Carter (1992) propose a second stage reestimation of the mortality index by holding and fixed, while searching for a new estimate satisfying the following equation
where Dt and are respectively the total number of deaths and the population age a in year t. Wilmoth (1993) suggests an alternative computational approach that estimates αa, βa, and kt simultaneously via weighted least squares, using the number of deaths at each age as weights
The first model this paper entertains is a variant of Lee-Carter, incorporating the bias corrections described in the previous paragraphs. Specifically, after some preliminary experimentation, a decision was made to settle on the following estimation approach: first, the model's parameters are computed by applying SVD on the matrix of centered logarithmic age profiles. Next, αa is set equal to the logarithm of the age-specific rates corresponding to the last period in the sample. Finally, a second stage reestimation of kt is performed to match total observed and fitted deaths.
A First-Order Autoregressive Approach
In a recent paper, Denton, Feaver, and Spencer (2005) suggest a number of multivariate time-series econometric specifications as alternatives to the Lee-Carter method. One such possibility is to model the first difference of logarithmic mortality as a pth-order autoregressive process AR (p):
Future changes in the individual mortality rates are determined by their own past values plus a random disturbance term . The age-specific series are estimated within a system of seemingly unrelated regression equations (SURE) to accommodate the significant contemporaneous correlation characterizing mortality data. Denton, Feavor, and Spencer (2005) further suggest a second specification, which they refer to as a quasi-vector autoregressive approach QVAR (p)
where Kt represents an index of mortality that is a function of all the individual age-specific mortality rates, much like in the Lee-Carter model.
The second model this paper entertains is a variant of equation (13) with p = 1 lags. Formally, let denote the annual rate of improvement in mortality expressed as the negative of the percent change in the central death rate:
Each series is then fitted individually to a first-order univariate autoregressive AR(1) model 4
Once parameter estimates , , and are computed, recursive substitution can generate forecasts of future rates in mortality improvement by iterating equation (15) forward
The process can be shown to be covariance stationary if , with mean and variance respectively equal to
For a covariance stationary process, the mean h-step-ahead forecast, conditional on the previous observations is given by
indicating that the projection decays geometrically from to the unconditional estimated mean , as the forecast horizon h increases. However, since each individual forecast ignores the typically high correlation among the age groups, the model is modified to accommodate a joint disturbance process. In particular, the estimated residuals are used to compute the following covariance matrix
where each column of S corresponds to the residuals obtained from each equation. Stochastic paths for the rates of mortality improvement are then generated by simulating random shock vectors from the multivariate normal distribution.
Data and Experimental Design
The data sets used to carry out the ex-post validation exercise proposed in this paper were obtained from the Human Mortality Database (HMD) and consist of mortality rates from 16 industrialized nations for males and females combined.5 Wilmoth (2004) documents the methods by which the raw data were converted into mortality rates. The investigation in this paper focuses on period death rates rather than cohort rates. In other words, the mortality rates are indexed by year of occurrence rather than year of birth, so that denotes mortality at age a occurring in year t, rather than the death rate of individuals aged a born in year t. While analysis of rates on a cohort basis might be preferable, a complete set of cohort mortalities requires a much longer time frame and can involve significant missing data problems.
Formally, the period death rate is defined as the ratio
where is the death count for the population in the age range [a, a + 1) on January 1st of calendar year t, while represents the exposure-to-risk (that is, the population exposed to the risk of death), measured as total person-years lived in the same age interval and time period. Generally, for a given country and year t, death counts and exposure-to-risk are available by single year of age from birth (age 0) to the open interval 110-years old and beyond (age 110 or older). Hence, to reduce the dimension of the forecasting problem and reasonably fit the data to the stochastic projection models, mortality rates were computed for the following 21 age groups: age 0, ages 1–4, ages 5–9,…, ages 90–94, ages 95 or older. The group rates were obtained by aggregating single year of age values. For instance, the resulting death rate for the 1–4 age group at time t was calculated as the ratio of total death counts for ages 1 through 4 over the sum of exposure-to- risk values for the same ages and time period.
Ex-post validation analysis involves using an initial portion of the available data to estimate a set of models that are then used to generate forecasts for the remaining time period. This way, it is possible to compare the models' projections to the actual observations to determine how well the models would have performed in the past. The design of any ex-post validation experiment always requires somewhat arbitrary decisions. For instance, the researcher must select the specific time frame and length over which the behavior of the models should be investigated, the fraction of the data used for estimation purposes, and the evaluation criteria employed to measure forecast performance. The particular objectives of the analysis shape these decisions and constrain the applicability of any conclusions. Table 1 lists the historical period of mortality data available for each of the 16 countries.6 The shortest sample corresponds to the United States (1959–2002) with 44 observations, while the longest sample belongs to Sweden (1751–2003), with 253 observations.
| Country | Data period |
Total observations |
Longest forecast horizons |
Total forecasts |
|---|---|---|---|---|
| Austria | 1947–2002 | 56 | 23 | 276 |
| Belgium | 1931–2002 | 72 | 23 | 276 |
| Canada | 1921–2002 | 82 | 23 | 276 |
| Denmark | 1835–2004 | 170 | 25 | 325 |
| Finland | 1878–2002 | 125 | 23 | 276 |
| France | 1899–2002 | 104 | 23 | 276 |
| Germany | 1956–2002 | 47 | 23 | 276 |
| Italy | 1872–2002 | 131 | 23 | 276 |
| Japan | 1950–2002 | 53 | 23 | 276 |
| Netherlands | 1850–2003 | 154 | 24 | 300 |
| Norway | 1846–2002 | 157 | 23 | 276 |
| Spain | 1908–2003 | 96 | 24 | 300 |
| Sweden | 1751–2003 | 253 | 24 | 300 |
| Switzerland | 1876–2004 | 129 | 25 | 325 |
| United Kingdom | 1841–2003 | 163 | 24 | 300 |
| United States | 1959–2002 | 44 | 23 | 276 |
| Source: Human Mortality Database. | ||||
This paper uses all available data regardless of potential country-specific concerns about variation in quality, particularly when the estimated mortality rates date back more than one century. This decision is justified by treating the selected stochastic models as general algorithms, whose mechanically-generated forecasts should be tested under multiple scenarios. Furthermore, to make the generated forecasts comparable across countries, the initial jump-off year (the first period to be forecast) is fixed to 1980 in all cases. This particular choice was made based on the shortest available data set, by roughly adhering to two guiding principles: First, for each series there should be at least as many in-sample observations as the length of the forecast horizon. Second, the estimation sample per series should be at least as large as the total number of variables to be projected (21 age groups).
To minimize the impact of the selected jump-off year on the resulting projections, it is common practice in out-of-sample validation exercises to focus on the forecast error corresponding to fixed lead times, using different forecast origins. In other words, for every country, each model is fitted using all observations from the beginning of the series until 1979 and mortality projections generated from 1980 to the end of the data set. Then, the sample is expanded to include the next observation (1980). Upon reestimation, new forecasts are generated from 1981 to the end of the series. This process is repeated until the only period left to forecast is the last available observation. For instance, for each age group in the United States, the projections generated over the various jump-off years (1980, 1981,…, 2001) yield a set of 23 forecasts involving a 1-year horizon, 22 forecasts involving a 2-year period, and eventually a single forecast 23 years ahead. The fourth column of Table 1 shows the size of the longest forecast horizon (from 1980 to the end of each series). By design, the analysis centers on evaluating forecast performance over the short- to medium-range (23 to 25-year horizons in most cases), a fact that is determined by the choice of initial jump-off year, given the small sample sizes of some of the data. The last column in Table 1 presents the total number of projected observations per age group, over all forecast horizons.
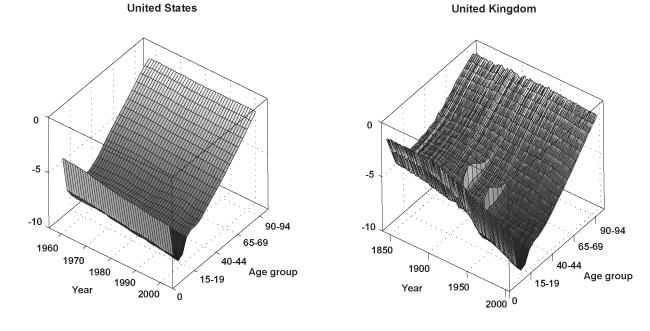
Chart 1 displays three-dimensional surfaces, as well as contours of the logarithmic age profile of mortality corresponding to the United States and the United Kingdom. They serve to illustrate a number of features in all-cause mortality common to most nations. One characteristic of the data is the regularity in the shape of mortality over the ages. For any given period, mortality declines smoothly from birth until about ages 10–14, then increases almost linearly for the remaining ages until death. Moreover, in the second half of the twentieth century, the death rates experience a sharp increase associated with motor-vehicle fatalities in the 15–19 age group, often referred to as "the accident hump." Notice also how the surface for the United Kingdom appears far less smooth than the one corresponding to the United States. The former contains a much longer data sample (1841–2003) that includes spikes in mortality associated with the two world wars and the 1918 Spanish influenza pandemic.
Surfaces and contours of the age profile of logarithmic mortality for the United States and the United Kingdom
| Year | 0 | 1–4 | 5–9 | 10–14 | 15–19 | 20–24 | 25–29 | 30–34 | 35–39 | 40–44 | 45–49 | 50–54 | 55–59 | 60–64 | 65–69 | 70–74 | 75–79 | 80–84 | 85–90 | 90–94 | 95 and older |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| United States | |||||||||||||||||||||
| 1959 | -3.6015 | -6.8416 | -7.6136 | -7.6905 | -6.9784 | -6.6849 | -6.6566 | -6.4148 | -6.0735 | -5.6217 | -5.1455 | -4.6819 | -4.2788 | -3.8687 | -3.4745 | -3.0754 | -2.644 | -2.1996 | -1.7665 | -1.3965 | -1.1108 |
| 1960 | -3.6169 | -6.8217 | -7.6255 | -7.7412 | -6.9952 | -6.7057 | -6.6357 | -6.4289 | -6.0574 | -5.6027 | -5.1321 | -4.6693 | -4.2842 | -3.8411 | -3.4619 | -3.0607 | -2.6375 | -2.1906 | -1.7618 | -1.3798 | -1.07 |
| 1961 | -3.6475 | -6.8894 | -7.6899 | -7.7651 | -7.0496 | -6.7258 | -6.6768 | -6.4423 | -6.077 | -5.6275 | -5.1637 | -4.6968 | -4.328 | -3.8629 | -3.4836 | -3.1005 | -2.6644 | -2.2147 | -1.7794 | -1.4063 | -1.0918 |
| 1962 | -3.6603 | -6.914 | -7.6911 | -7.7833 | -7.0289 | -6.7061 | -6.6616 | -6.4348 | -6.047 | -5.619 | -5.1494 | -4.6833 | -4.3132 | -3.8526 | -3.4711 | -3.0915 | -2.6482 | -2.2014 | -1.7552 | -1.3851 | -1.0545 |
| 1963 | -3.6619 | -6.8919 | -7.6986 | -7.7947 | -7.0096 | -6.6883 | -6.6292 | -6.4176 | -6.0282 | -5.6073 | -5.1345 | -4.6762 | -4.2911 | -3.8352 | -3.4628 | -3.0746 | -2.6325 | -2.1886 | -1.7404 | -1.3624 | -1.0272 |
| 1964 | -3.6735 | -6.9216 | -7.7128 | -7.7854 | -6.9701 | -6.6752 | -6.6193 | -6.381 | -6.0235 | -5.5995 | -5.1481 | -4.684 | -4.3152 | -3.8481 | -3.4966 | -3.1113 | -2.6671 | -2.229 | -1.7875 | -1.4094 | -1.0892 |
| 1965 | -3.7039 | -6.9456 | -7.7305 | -7.8096 | -6.9575 | -6.667 | -6.6172 | -6.3899 | -6.0219 | -5.5978 | -5.1447 | -4.6837 | -4.3152 | -3.8544 | -3.4914 | -3.1171 | -2.6619 | -2.2277 | -1.7813 | -1.4056 | -1.084 |
| 1966 | -3.7379 | -6.9419 | -7.718 | -7.7965 | -6.8746 | -6.6331 | -6.598 | -6.3772 | -6.0239 | -5.5864 | -5.1347 | -4.6835 | -4.3009 | -3.8655 | -3.4859 | -3.1024 | -2.6618 | -2.2283 | -1.7882 | -1.4018 | -1.0823 |
| 1967 | -3.7805 | -7.0194 | -7.7527 | -7.8103 | -6.8923 | -6.6058 | -6.5985 | -6.39 | -6.0096 | -5.598 | -5.1455 | -4.7046 | -4.3108 | -3.8907 | -3.5112 | -3.1196 | -2.6903 | -2.2582 | -1.8184 | -1.4295 | -1.1225 |
| 1968 | -3.7996 | -7.0166 | -7.7175 | -7.7833 | -6.8298 | -6.556 | -6.546 | -6.3596 | -5.985 | -5.5637 | -5.1191 | -4.6878 | -4.2815 | -3.8667 | -3.4808 | -3.0941 | -2.665 | -2.239 | -1.7984 | -1.3979 | -1.0904 |
| 1969 | -3.823 | -7.04 | -7.7272 | -7.7902 | -6.7829 | -6.5193 | -6.5343 | -6.352 | -5.9826 | -5.5604 | -5.1367 | -4.7193 | -4.2966 | -3.9046 | -3.5019 | -3.1213 | -2.696 | -2.2642 | -1.8282 | -1.4335 | -1.1075 |
| 1970 | -3.8522 | -7.0805 | -7.7682 | -7.8116 | -6.8164 | -6.5325 | -6.5477 | -6.3693 | -6.0012 | -5.5785 | -5.1424 | -4.7276 | -4.2997 | -3.9163 | -3.5212 | -3.134 | -2.7144 | -2.3008 | -1.8732 | -1.4792 | -1.1574 |
| 1971 | -3.9446 | -7.105 | -7.7735 | -7.8224 | -6.8097 | -6.5306 | -6.5552 | -6.386 | -6.0226 | -5.6046 | -5.1685 | -4.755 | -4.3247 | -3.9352 | -3.5575 | -3.1453 | -2.7249 | -2.3112 | -1.8655 | -1.4728 | -1.1345 |
| 1972 | -4.017 | -7.1213 | -7.8045 | -7.8134 | -6.8078 | -6.5349 | -6.5589 | -6.3952 | -6.0484 | -5.6145 | -5.16 | -4.7645 | -4.3261 | -3.9318 | -3.5501 | -3.1287 | -2.7184 | -2.3069 | -1.8735 | -1.483 | -1.1236 |
| 1973 | -4.0415 | -7.1388 | -7.7978 | -7.8165 | -6.8024 | -6.5349 | -6.5633 | -6.4069 | -6.0543 | -5.6398 | -5.1778 | -4.7859 | -4.3398 | -3.9501 | -3.5766 | -3.147 | -2.7397 | -2.312 | -1.8731 | -1.4723 | -1.1064 |
| 1974 | -4.0759 | -7.216 | -7.8995 | -7.8654 | -6.8597 | -6.5889 | -6.6087 | -6.4604 | -6.1275 | -5.6854 | -5.22 | -4.8157 | -4.3935 | -3.9822 | -3.6174 | -3.1719 | -2.7929 | -2.3507 | -1.9074 | -1.5096 | -1.137 |
| 1975 | -4.1254 | -7.2659 | -7.9571 | -7.9444 | -6.9056 | -6.5987 | -6.619 | -6.5065 | -6.1706 | -5.7293 | -5.272 | -4.8466 | -4.4326 | -4.0171 | -3.6608 | -3.2099 | -2.8372 | -2.3994 | -1.9747 | -1.5693 | -1.1955 |
| 1976 | -4.1851 | -7.2859 | -7.979 | -7.9805 | -6.9482 | -6.654 | -6.6627 | -6.5709 | -6.226 | -5.7674 | -5.3006 | -4.8662 | -4.4572 | -4.0245 | -3.6762 | -3.2365 | -2.8506 | -2.4073 | -1.9644 | -1.5456 | -1.1597 |
| 1977 | -4.2383 | -7.3056 | -8.0064 | -7.9692 | -6.9086 | -6.6389 | -6.6652 | -6.5731 | -6.2447 | -5.796 | -5.3335 | -4.8864 | -4.4881 | -4.0496 | -3.7006 | -3.2589 | -2.8876 | -2.4371 | -2.0087 | -1.5917 | -1.2138 |
| 1978 | -4.2874 | -7.2962 | -8.0248 | -7.9957 | -6.9178 | -6.6318 | -6.6665 | -6.5986 | -6.2663 | -5.8244 | -5.3554 | -4.9008 | -4.5097 | -4.0596 | -3.7087 | -3.2738 | -2.9001 | -2.4418 | -2.006 | -1.5865 | -1.1919 |
| 1979 | -4.3216 | -7.3517 | -8.074 | -8.0563 | -6.918 | -6.6367 | -6.646 | -6.5979 | -6.2929 | -5.8668 | -5.3963 | -4.9338 | -4.5369 | -4.103 | -3.732 | -3.3125 | -2.9288 | -2.473 | -2.0419 | -1.6312 | -1.2302 |
| 1980 | -4.3556 | -7.3642 | -8.0884 | -8.0894 | -6.9217 | -6.6278 | -6.6394 | -6.5874 | -6.3044 | -5.8806 | -5.4058 | -4.9422 | -4.5217 | -4.1094 | -3.7075 | -3.3042 | -2.9091 | -2.4476 | -2.0109 | -1.5858 | -1.1757 |
| 1981 | -4.4222 | -7.4086 | -8.1456 | -8.1245 | -7.0123 | -6.6992 | -6.6627 | -6.5889 | -6.3335 | -5.9115 | -5.4258 | -4.9666 | -4.5356 | -4.1321 | -3.728 | -3.3282 | -2.9425 | -2.4736 | -2.0353 | -1.622 | -1.2091 |
| 1982 | -4.4517 | -7.4494 | -8.1706 | -8.1735 | -7.0642 | -6.7674 | -6.7352 | -6.6347 | -6.3736 | -5.9702 | -5.4737 | -5.0015 | -4.5621 | -4.144 | -3.7424 | -3.343 | -2.9454 | -2.4939 | -2.0612 | -1.6576 | -1.2359 |
| 1983 | -4.4931 | -7.4836 | -8.2364 | -8.2022 | -7.1175 | -6.8299 | -6.7724 | -6.6538 | -6.4142 | -5.9891 | -5.5094 | -5.0108 | -4.5591 | -4.1437 | -3.7477 | -3.335 | -2.9377 | -2.4872 | -2.045 | -1.6254 | -1.2075 |
| 1984 | -4.5149 | -7.5547 | -8.2799 | -8.1701 | -7.127 | -6.8144 | -6.7843 | -6.6336 | -6.3928 | -5.9856 | -5.5231 | -5.0338 | -4.5744 | -4.1493 | -3.7594 | -3.3431 | -2.9483 | -2.5007 | -2.0522 | -1.6308 | -1.2038 |
| 1985 | -4.5171 | -7.5649 | -8.2946 | -8.1781 | -7.1267 | -6.8325 | -6.7757 | -6.6047 | -6.3642 | -5.9856 | -5.5254 | -5.0411 | -4.5798 | -4.1514 | -3.7645 | -3.3412 | -2.9443 | -2.4948 | -2.0404 | -1.61 | -1.1927 |
| 1986 | -4.5543 | -7.5521 | -8.3391 | -8.1636 | -7.0532 | -6.7731 | -6.7151 | -6.5263 | -6.306 | -5.9836 | -5.5452 | -5.0592 | -4.6133 | -4.1632 | -3.7765 | -3.3484 | -2.9569 | -2.5132 | -2.0577 | -1.621 | -1.1944 |
| 1987 | -4.57 | -7.5595 | -8.3073 | -8.213 | -7.0869 | -6.8023 | -6.7141 | -6.5108 | -6.2846 | -5.9957 | -5.5583 | -5.0683 | -4.6229 | -4.1767 | -3.7872 | -3.3649 | -2.9697 | -2.5263 | -2.0653 | -1.6229 | -1.1779 |
| 1988 | -4.5735 | -7.573 | -8.3104 | -8.1936 | -7.0478 | -6.7893 | -6.697 | -6.4936 | -6.2525 | -5.9867 | -5.5602 | -5.0927 | -4.6226 | -4.1828 | -3.7926 | -3.3748 | -2.9719 | -2.5181 | -2.0545 | -1.6023 | -1.157 |
| 1989 | -4.5804 | -7.6043 | -8.3318 | -8.2026 | -7.0598 | -6.8262 | -6.684 | -6.4684 | -6.2427 | -5.9775 | -5.576 | -5.1157 | -4.6442 | -4.2117 | -3.8168 | -3.4063 | -2.9962 | -2.5539 | -2.0955 | -1.6427 | -1.1731 |
| 1990 | -4.6411 | -7.6712 | -8.4158 | -8.2652 | -7.0262 | -6.8138 | -6.6811 | -6.4857 | -6.2364 | -5.996 | -5.5865 | -5.1415 | -4.6729 | -4.2297 | -3.8337 | -3.4299 | -3.0167 | -2.5784 | -2.1208 | -1.6619 | -1.2055 |
| 1991 | -4.6906 | -7.6528 | -8.4438 | -8.2693 | -7.0299 | -6.8104 | -6.7069 | -6.4804 | -6.23 | -5.9656 | -5.5947 | -5.1622 | -4.6847 | -4.2466 | -3.8454 | -3.4425 | -3.036 | -2.5934 | -2.1349 | -1.6714 | -1.2018 |
| 1992 | -4.7396 | -7.7403 | -8.5036 | -8.317 | -7.0886 | -6.8579 | -6.7365 | -6.4876 | -6.2223 | -5.9497 | -5.6001 | -5.1829 | -4.713 | -4.2696 | -3.8596 | -3.4588 | -3.054 | -2.6173 | -2.1529 | -1.6931 | -1.2187 |
| 1993 | -4.7592 | -7.7127 | -8.469 | -8.2789 | -7.062 | -6.8305 | -6.7245 | -6.4528 | -6.1934 | -5.918 | -5.6031 | -5.1762 | -4.715 | -4.2606 | -3.8504 | -3.4502 | -3.0334 | -2.593 | -2.1167 | -1.6528 | -1.1596 |
| 1994 | -4.798 | -7.7571 | -8.5322 | -8.3009 | -7.0634 | -6.8409 | -6.739 | -6.4436 | -6.18 | -5.905 | -5.5938 | -5.1803 | -4.7409 | -4.2772 | -3.8715 | -3.4632 | -3.0562 | -2.6044 | -2.1349 | -1.663 | -1.1731 |
| 1995 | -4.8538 | -7.8137 | -8.5445 | -8.2901 | -7.1054 | -6.8595 | -6.7673 | -6.4554 | -6.182 | -5.8937 | -5.5969 | -5.1876 | -4.7526 | -4.2897 | -3.8887 | -3.468 | -3.059 | -2.6074 | -2.1334 | -1.6592 | -1.1575 |
| 1996 | -4.8831 | -7.8754 | -8.5661 | -8.3575 | -7.1633 | -6.9152 | -6.8636 | -6.5788 | -6.2836 | -5.962 | -5.6151 | -5.2332 | -4.7776 | -4.3024 | -3.9068 | -3.4764 | -3.0683 | -2.6115 | -2.1452 | -1.6647 | -1.162 |
| 1997 | -4.8953 | -7.9438 | -8.6215 | -8.3987 | -7.2138 | -6.9452 | -6.9387 | -6.7045 | -6.3951 | -6.0323 | -5.6644 | -5.2608 | -4.8042 | -4.3344 | -3.9225 | -3.4922 | -3.0805 | -2.6183 | -2.1548 | -1.665 | -1.1684 |
| 1998 | -4.889 | -7.9831 | -8.6661 | -8.4463 | -7.2694 | -6.9851 | -6.9938 | -6.7564 | -6.422 | -6.0456 | -5.6794 | -5.2965 | -4.8286 | -4.362 | -3.9316 | -3.4966 | -3.0885 | -2.6117 | -2.1579 | -1.6749 | -1.1688 |
| 1999 | -4.913 | -7.9808 | -8.6865 | -8.4981 | -7.2849 | -7.0037 | -7.0088 | -6.7825 | -6.4317 | -6.0466 | -5.6663 | -5.2966 | -4.829 | -4.3766 | -3.9363 | -3.508 | -3.0778 | -2.6069 | -2.1317 | -1.6564 | -1.1491 |
| 2000 | -4.9365 | -8.0312 | -8.7466 | -8.507 | -7.3075 | -6.9839 | -6.9939 | -6.8059 | -6.4401 | -6.0394 | -5.6552 | -5.2923 | -4.8438 | -4.3949 | -3.959 | -3.5294 | -3.0914 | -2.6213 | -2.1385 | -1.6675 | -1.164 |
| 2001 | -4.9786 | -8.0093 | -8.7854 | -8.5597 | -7.3108 | -6.9646 | -6.9486 | -6.7823 | -6.4021 | -6.0314 | -5.6407 | -5.276 | -4.8607 | -4.4151 | -3.9798 | -3.549 | -3.1055 | -2.638 | -2.1445 | -1.697 | -1.1909 |
| 2002 | -4.9619 | -8.073 | -8.7967 | -8.5374 | -7.2954 | -6.963 | -6.9602 | -6.7893 | -6.4254 | -6.0181 | -5.6339 | -5.2728 | -4.8658 | -4.4287 | -4.0016 | -3.5606 | -3.1163 | -2.6435 | -2.1448 | -1.7063 | -1.2167 |
| United Kingdom | |||||||||||||||||||||
| 1841 | -1.8788 | -3.3091 | -4.6622 | -5.2491 | -4.883 | -4.7013 | -4.6133 | -4.605 | -4.3986 | -4.4061 | -4.1325 | -4.068 | -3.5717 | -3.5036 | -2.9264 | -2.6775 | -2.1497 | -1.8825 | -1.5327 | -1.2119 | -0.9122 |
| 1842 | -1.7929 | -3.3075 | -4.6986 | -5.2711 | -4.9109 | -4.717 | -4.6506 | -4.6317 | -4.4287 | -4.399 | -4.17 | -4.0755 | -3.6371 | -3.4656 | -2.9402 | -2.6215 | -2.1492 | -1.8869 | -1.5383 | -1.2067 | -0.8602 |
| 1843 | -1.7941 | -3.3495 | -4.7605 | -5.3264 | -4.969 | -4.7271 | -4.6849 | -4.6359 | -4.4457 | -4.3568 | -4.2144 | -4.0637 | -3.7204 | -3.4161 | -3.0069 | -2.5968 | -2.202 | -1.9063 | -1.5578 | -1.226 | -0.8891 |
| 1844 | -1.8067 | -3.3307 | -4.6907 | -5.3161 | -4.9735 | -4.698 | -4.6674 | -4.6075 | -4.4782 | -4.3385 | -4.2308 | -4.0004 | -3.7524 | -3.3395 | -3.0246 | -2.5349 | -2.1937 | -1.8687 | -1.5075 | -1.1675 | -0.8272 |
| 1845 | -1.8588 | -3.3687 | -4.7917 | -5.3526 | -4.9638 | -4.6815 | -4.6909 | -4.6245 | -4.5126 | -4.3277 | -4.2821 | -4.0003 | -3.8263 | -3.327 | -3.0906 | -2.544 | -2.2397 | -1.8938 | -1.5365 | -1.2035 | -0.8783 |
| 1846 | -1.6922 | -3.2382 | -4.784 | -5.2508 | -4.8946 | -4.5978 | -4.6046 | -4.5418 | -4.4666 | -4.273 | -4.2387 | -3.9304 | -3.7936 | -3.2719 | -3.0463 | -2.4995 | -2.1872 | -1.8389 | -1.4549 | -1.0844 | -0.6868 |
| 1847 | -1.7284 | -3.202 | -4.6234 | -5.1622 | -4.8273 | -4.5312 | -4.5139 | -4.4338 | -4.3333 | -4.144 | -4.0898 | -3.7941 | -3.6154 | -3.1502 | -2.8765 | -2.3952 | -2.007 | -1.672 | -1.3171 | -1.0005 | -0.7133 |
| 1848 | -1.7525 | -3.2118 | -4.5706 | -5.191 | -4.8937 | -4.6025 | -4.579 | -4.5184 | -4.4132 | -4.2591 | -4.18 | -3.9324 | -3.6972 | -3.3124 | -2.9593 | -2.5638 | -2.1244 | -1.8114 | -1.4527 | -1.1178 | -0.7992 |
| 1849 | -1.7232 | -3.2332 | -4.4871 | -5.0222 | -4.7802 | -4.4875 | -4.3898 | -4.2996 | -4.1912 | -4.0656 | -3.9393 | -3.7515 | -3.501 | -3.2292 | -2.8353 | -2.522 | -2.0773 | -1.7881 | -1.4557 | -1.1146 | -0.7571 |
| 1850 | -1.8363 | -3.407 | -4.8072 | -5.333 | -5.0109 | -4.7897 | -4.714 | -4.6307 | -4.4969 | -4.383 | -4.2214 | -4.0505 | -3.711 | -3.4583 | -2.9707 | -2.6529 | -2.1754 | -1.8649 | -1.522 | -1.1827 | -0.8403 |
| 1851 | -1.7705 | -3.3191 | -4.7418 | -5.283 | -4.9431 | -4.7271 | -4.6663 | -4.5969 | -4.4515 | -4.3455 | -4.1719 | -4.0277 | -3.6768 | -3.4433 | -2.9524 | -2.6275 | -2.1801 | -1.8631 | -1.529 | -1.1875 | -0.8216 |
| 1852 | -1.7338 | -3.3123 | -4.695 | -5.2498 | -4.9043 | -4.698 | -4.6387 | -4.5794 | -4.445 | -4.3422 | -4.1697 | -4.0175 | -3.6855 | -3.4294 | -3.0021 | -2.6315 | -2.1868 | -1.8347 | -1.5065 | -1.183 | -0.8601 |
| 1853 | -1.7431 | -3.3373 | -4.7542 | -5.2625 | -4.8717 | -4.6497 | -4.5986 | -4.5423 | -4.411 | -4.2868 | -4.1158 | -3.9427 | -3.6513 | -3.3388 | -2.9481 | -2.5283 | -2.1053 | -1.7369 | -1.4128 | -1.1068 | -0.8107 |
| 1854 | -1.7397 | -3.1898 | -4.6331 | -5.1981 | -4.8822 | -4.6252 | -4.5746 | -4.5091 | -4.3787 | -4.2384 | -4.0985 | -3.9148 | -3.6797 | -3.3285 | -2.9918 | -2.5496 | -2.1651 | -1.7981 | -1.4956 | -1.2163 | -0.9527 |
| 1855 | -1.777 | -3.341 | -4.7711 | -5.3056 | -4.953 | -4.6825 | -4.657 | -4.5865 | -4.4454 | -4.2837 | -4.1728 | -3.9349 | -3.6884 | -3.2595 | -2.949 | -2.4634 | -2.0728 | -1.6796 | -1.3382 | -1.032 | -0.7526 |
| 1856 | -1.8307 | -3.4087 | -4.8885 | -5.3918 | -5.0329 | -4.7537 | -4.7243 | -4.6517 | -4.5339 | -4.3687 | -4.2763 | -4.0313 | -3.8324 | -3.3965 | -3.1027 | -2.6379 | -2.2711 | -1.8989 | -1.5729 | -1.2684 | -0.984 |
| 1857 | -1.7596 | -3.3373 | -4.833 | -5.3551 | -5.0162 | -4.7317 | -4.7051 | -4.6365 | -4.525 | -4.3499 | -4.2432 | -3.9861 | -3.7838 | -3.3591 | -3.0253 | -2.5833 | -2.176 | -1.8087 | -1.4766 | -1.1613 | -0.859 |
| 1858 | -1.747 | -3.1902 | -4.5398 | -5.2485 | -4.9714 | -4.7056 | -4.6769 | -4.6096 | -4.4917 | -4.3312 | -4.2205 | -3.9805 | -3.7476 | -3.3557 | -2.9658 | -2.5603 | -2.1269 | -1.7737 | -1.4276 | -1.0967 | -0.777 |
| 1859 | -1.7476 | -3.2488 | -4.6622 | -5.2816 | -5.0086 | -4.7542 | -4.6899 | -4.6127 | -4.4881 | -4.3464 | -4.202 | -3.9857 | -3.7283 | -3.4074 | -2.981 | -2.6204 | -2.1743 | -1.8364 | -1.5047 | -1.1802 | -0.8607 |
| 1860 | -1.8342 | -3.431 | -4.9741 | -5.4511 | -5.0554 | -4.8089 | -4.7204 | -4.6279 | -4.4763 | -4.3645 | -4.2055 | -4.003 | -3.6671 | -3.3896 | -2.9129 | -2.5759 | -2.1088 | -1.7719 | -1.4469 | -1.1297 | -0.8122 |
| 1861 | -1.7899 | -3.3248 | -4.9914 | -5.4398 | -5.0009 | -4.8047 | -4.7151 | -4.6293 | -4.4803 | -4.3942 | -4.2213 | -4.0305 | -3.6689 | -3.4258 | -2.9562 | -2.622 | -2.1564 | -1.811 | -1.4976 | -1.208 | -0.9548 |
| 1862 | -1.8437 | -3.3189 | -4.8713 | -5.4119 | -5.0281 | -4.8235 | -4.7248 | -4.6277 | -4.4666 | -4.373 | -4.206 | -4.0131 | -3.6715 | -3.4077 | -2.9843 | -2.627 | -2.2027 | -1.8505 | -1.5361 | -1.2358 | -0.9558 |
| 1863 | -1.8051 | -3.141 | -4.5706 | -5.2903 | -5.016 | -4.7848 | -4.7001 | -4.6026 | -4.4404 | -4.3397 | -4.2093 | -4.0037 | -3.6816 | -3.3773 | -3.0107 | -2.6202 | -2.2234 | -1.8538 | -1.5117 | -1.1676 | -0.8157 |
| 1864 | -1.7768 | -3.236 | -4.6084 | -5.3014 | -4.9911 | -4.7206 | -4.6342 | -4.5215 | -4.3665 | -4.2418 | -4.1212 | -3.8882 | -3.5991 | -3.2515 | -2.9206 | -2.4997 | -2.14 | -1.7729 | -1.4422 | -1.1076 | -0.7582 |
| 1865 | -1.7281 | -3.3318 | -4.8045 | -5.3721 | -5.0156 | -4.7048 | -4.6277 | -4.5143 | -4.3814 | -4.2365 | -4.1204 | -3.868 | -3.6323 | -3.2663 | -2.9765 | -2.5199 | -2.1586 | -1.7721 | -1.4476 | -1.1272 | -0.8051 |
| 1866 | -1.7304 | -3.3118 | -4.8618 | -5.3926 | -5.014 | -4.6936 | -4.6029 | -4.4673 | -4.3424 | -4.1922 | -4.0992 | -3.8433 | -3.6335 | -3.252 | -2.9659 | -2.5081 | -2.1474 | -1.767 | -1.4431 | -1.121 | -0.7876 |
| 1867 | -1.7686 | -3.4742 | -5.0474 | -5.5364 | -5.088 | -4.7923 | -4.7027 | -4.5586 | -4.4347 | -4.2821 | -4.1885 | -3.9248 | -3.6879 | -3.2997 | -2.9757 | -2.5339 | -2.1291 | -1.7502 | -1.4291 | -1.1282 | -0.8432 |
| 1868 | -1.7459 | -3.3567 | -4.8723 | -5.4708 | -5.1122 | -4.8183 | -4.7149 | -4.5775 | -4.4643 | -4.32 | -4.201 | -3.959 | -3.7134 | -3.3689 | -3.0218 | -2.6296 | -2.2082 | -1.8471 | -1.5501 | -1.2642 | -0.9869 |
| 1869 | -1.7635 | -3.3334 | -4.8234 | -5.4383 | -5.1422 | -4.8602 | -4.7234 | -4.5727 | -4.4425 | -4.3049 | -4.1552 | -3.9396 | -3.6618 | -3.3407 | -2.938 | -2.5719 | -2.1308 | -1.7779 | -1.4894 | -1.2206 | -0.9769 |
| 1870 | -1.7377 | -3.3091 | -4.7553 | -5.3933 | -5.0885 | -4.8421 | -4.6974 | -4.5516 | -4.4095 | -4.2976 | -4.1338 | -3.9439 | -3.6123 | -3.3272 | -2.8996 | -2.5609 | -2.0959 | -1.7367 | -1.4435 | -1.1757 | -0.9491 |
| 1871 | -1.7572 | -3.3747 | -4.8335 | -5.4175 | -5.0339 | -4.7443 | -4.6201 | -4.516 | -4.3674 | -4.2693 | -4.0999 | -3.9411 | -3.6063 | -3.3375 | -2.9056 | -2.5798 | -2.1393 | -1.7819 | -1.4835 | -1.2013 | -0.9449 |
| 1872 | -1.7824 | -3.4936 | -4.9708 | -5.5147 | -5.0984 | -4.8042 | -4.6741 | -4.5742 | -4.4011 | -4.2909 | -4.1339 | -3.9841 | -3.6754 | -3.3769 | -2.9634 | -2.6153 | -2.2081 | -1.8364 | -1.5408 | -1.2586 | -0.9955 |
| 1873 | -1.8056 | -3.5664 | -5.1145 | -5.6361 | -5.2145 | -4.933 | -4.7667 | -4.6415 | -4.4507 | -4.3001 | -4.127 | -3.9436 | -3.6569 | -3.3035 | -2.8979 | -2.5198 | -2.1501 | -1.7673 | -1.4463 | -1.1351 | -0.8158 |
| 1874 | -1.7825 | -3.4056 | -4.8818 | -5.5557 | -5.2078 | -4.8887 | -4.7252 | -4.5979 | -4.403 | -4.2346 | -4.0934 | -3.8907 | -3.6302 | -3.2538 | -2.8973 | -2.5134 | -2.1762 | -1.7876 | -1.4715 | -1.1616 | -0.8429 |
| 1875 | -1.748 | -3.4553 | -4.9777 | -5.5822 | -5.1869 | -4.8821 | -4.7242 | -4.575 | -4.3797 | -4.1864 | -4.0626 | -3.8278 | -3.5865 | -3.183 | -2.8562 | -2.4397 | -2.0776 | -1.6496 | -1.3251 | -1.0198 | -0.7335 |
| 1876 | -1.802 | -3.5358 | -5.0671 | -5.6327 | -5.2579 | -4.9413 | -4.8033 | -4.6461 | -4.4562 | -4.248 | -4.1465 | -3.9048 | -3.6891 | -3.2816 | -2.9605 | -2.5521 | -2.1987 | -1.7787 | -1.4649 | -1.1612 | -0.8623 |
| 1877 | -1.8984 | -3.5647 | -5.127 | -5.633 | -5.3171 | -4.9924 | -4.8285 | -4.6513 | -4.4835 | -4.273 | -4.161 | -3.9106 | -3.6878 | -3.2944 | -2.9431 | -2.5538 | -2.1897 | -1.784 | -1.4448 | -1.1062 | -0.7492 |
| 1878 | -1.7791 | -3.4231 | -5.0502 | -5.6119 | -5.3114 | -5.0148 | -4.8656 | -4.6714 | -4.4891 | -4.2796 | -4.1519 | -3.9018 | -3.6375 | -3.2809 | -2.9062 | -2.5259 | -2.1141 | -1.6963 | -1.3502 | -1.0153 | -0.6834 |
| 1879 | -1.9052 | -3.5208 | -5.1065 | -5.686 | -5.3595 | -5.075 | -4.8923 | -4.674 | -4.4961 | -4.3021 | -4.1289 | -3.8782 | -3.5671 | -3.2461 | -2.83 | -2.4551 | -2.0224 | -1.6033 | -1.2664 | -0.9467 | -0.6385 |
| 1880 | -1.7985 | -3.4049 | -5.0803 | -5.7062 | -5.3736 | -5.1102 | -4.9596 | -4.7481 | -4.5447 | -4.3755 | -4.1856 | -3.9703 | -3.6305 | -3.3649 | -2.9256 | -2.571 | -2.1529 | -1.7446 | -1.4192 | -1.0949 | -0.7726 |
| 1881 | -1.9587 | -3.6727 | -5.1575 | -5.7351 | -5.3746 | -5.1089 | -4.9287 | -4.71 | -4.4918 | -4.3599 | -4.1731 | -3.9715 | -3.6046 | -3.3588 | -2.9342 | -2.5812 | -2.1731 | -1.7647 | -1.4728 | -1.1726 | -0.871 |
| 1882 | -1.8681 | -3.5145 | -5.083 | -5.7369 | -5.3573 | -5.1326 | -4.9278 | -4.7185 | -4.5018 | -4.3793 | -4.1793 | -3.9655 | -3.6238 | -3.3597 | -2.976 | -2.6037 | -2.2079 | -1.7973 | -1.5076 | -1.2128 | -0.9183 |
| 1883 | -1.8962 | -3.6174 | -5.1023 | -5.7159 | -5.3189 | -5.0902 | -4.9066 | -4.7171 | -4.479 | -4.3441 | -4.1521 | -3.9193 | -3.6047 | -3.2988 | -2.9439 | -2.5385 | -2.1411 | -1.7203 | -1.4381 | -1.1655 | -0.9157 |
| 1884 | -1.8183 | -3.5825 | -5.1268 | -5.7407 | -5.3558 | -5.1195 | -4.9281 | -4.7435 | -4.5084 | -4.3565 | -4.1682 | -3.9238 | -3.6634 | -3.3277 | -2.9905 | -2.5644 | -2.1879 | -1.7753 | -1.515 | -1.28 | -1.1012 |
| 1885 | -1.8973 | -3.6504 | -5.2688 | -5.8157 | -5.4044 | -5.1504 | -4.9514 | -4.756 | -4.524 | -4.3569 | -4.1907 | -3.9116 | -3.6571 | -3.2758 | -2.9498 | -2.5043 | -2.1359 | -1.7198 | -1.4211 | -1.1432 | -0.8891 |
| 1886 | -1.8037 | -3.6379 | -5.3407 | -5.8385 | -5.4326 | -5.1902 | -5.0157 | -4.8112 | -4.5792 | -4.3791 | -4.2148 | -3.9062 | -3.6561 | -3.2581 | -2.9278 | -2.4858 | -2.1113 | -1.6923 | -1.345 | -1.0149 | -0.6792 |
| 1887 | -1.8443 | -3.6276 | -5.2844 | -5.8362 | -5.4749 | -5.1986 | -5.0447 | -4.8353 | -4.6026 | -4.381 | -4.2249 | -3.9143 | -3.6538 | -3.2705 | -2.9206 | -2.514 | -2.1311 | -1.7247 | -1.4046 | -1.1065 | -0.8231 |
| 1888 | -1.8987 | -3.7336 | -5.3684 | -5.8794 | -5.5221 | -5.2195 | -5.0671 | -4.8551 | -4.6386 | -4.4027 | -4.2302 | -3.9352 | -3.6643 | -3.3067 | -2.919 | -2.5432 | -2.1479 | -1.7456 | -1.4086 | -1.0926 | -0.7933 |
| 1889 | -1.8398 | -3.6299 | -5.3675 | -5.9086 | -5.555 | -5.2799 | -5.1192 | -4.8895 | -4.6696 | -4.4329 | -4.2539 | -3.9815 | -3.675 | -3.3466 | -2.9371 | -2.5926 | -2.1884 | -1.7869 | -1.4396 | -1.1085 | -0.7906 |
| 1890 | -1.8216 | -3.6015 | -5.3107 | -5.8571 | -5.475 | -5.2097 | -5.017 | -4.7685 | -4.5374 | -4.3013 | -4.1002 | -3.8565 | -3.5198 | -3.235 | -2.8241 | -2.5109 | -2.1048 | -1.7027 | -1.3647 | -1.0374 | -0.7227 |
| 1891 | -1.7947 | -3.6118 | -5.3532 | -5.8982 | -5.4679 | -5.224 | -5.0204 | -4.7791 | -4.5236 | -4.2829 | -4.042 | -3.8111 | -3.4459 | -3.1512 | -2.7275 | -2.4108 | -2.0183 | -1.6089 | -1.2682 | -0.9341 | -0.5938 |
| 1892 | -1.8186 | -3.6404 | -5.3524 | -5.9477 | -5.5327 | -5.3184 | -5.0917 | -4.8661 | -4.5955 | -4.3783 | -4.1382 | -3.927 | -3.5636 | -3.2217 | -2.7995 | -2.4522 | -2.0816 | -1.6529 | -1.309 | -0.9811 | -0.6655 |
| 1893 | -1.735 | -3.675 | -5.2562 | -5.853 | -5.4574 | -5.2601 | -5.0386 | -4.834 | -4.5544 | -4.3547 | -4.1308 | -3.9379 | -3.608 | -3.2447 | -2.8581 | -2.502 | -2.1737 | -1.7414 | -1.4081 | -1.0677 | -0.7094 |
| 1894 | -1.9085 | -3.79 | -5.4241 | -6.0278 | -5.6086 | -5.3625 | -5.1598 | -4.981 | -4.7067 | -4.4996 | -4.2636 | -4.0548 | -3.7574 | -3.373 | -3.0106 | -2.6344 | -2.312 | -1.8616 | -1.5488 | -1.2291 | -0.9069 |
| 1895 | -1.7182 | -3.6959 | -5.4605 | -5.9996 | -5.6088 | -5.3602 | -5.1571 | -4.9612 | -4.6901 | -4.4621 | -4.2144 | -3.9469 | -3.6429 | -3.2259 | -2.8854 | -2.4834 | -2.1299 | -1.6414 | -1.3258 | -1.022 | -0.7608 |
| 1896 | -1.8185 | -3.6888 | -5.3829 | -6.0415 | -5.6843 | -5.4178 | -5.2333 | -5.0146 | -4.7457 | -4.503 | -4.2885 | -4.017 | -3.7604 | -3.349 | -3.0152 | -2.6378 | -2.3138 | -1.8527 | -1.5282 | -1.1804 | -0.8188 |
| 1897 | -1.7569 | -3.7757 | -5.5096 | -6.0454 | -5.6777 | -5.4153 | -5.2354 | -4.9951 | -4.7486 | -4.4933 | -4.2889 | -3.9929 | -3.7366 | -3.3346 | -2.9775 | -2.6069 | -2.2393 | -1.7791 | -1.4731 | -1.1485 | -0.8174 |
| 1898 | -1.7243 | -3.7734 | -5.5573 | -6.0933 | -5.7079 | -5.4225 | -5.2563 | -5.0006 | -4.757 | -4.4913 | -4.292 | -3.99 | -3.7196 | -3.3372 | -2.9511 | -2.5981 | -2.212 | -1.77 | -1.455 | -1.1323 | -0.8057 |
| 1899 | -1.7045 | -3.7995 | -5.4787 | -6.0314 | -5.6803 | -5.3915 | -5.2231 | -4.9535 | -4.6983 | -4.4216 | -4.2073 | -3.9158 | -3.6325 | -3.2826 | -2.8678 | -2.5232 | -2.1252 | -1.6972 | -1.3927 | -1.0985 | -0.8146 |
| 1900 | -1.7791 | -3.7567 | -5.4683 | -6.0237 | -5.6575 | -5.379 | -5.2118 | -4.9542 | -4.6949 | -4.4234 | -4.1841 | -3.894 | -3.5666 | -3.2582 | -2.8397 | -2.5047 | -2.1014 | -1.6736 | -1.3834 | -1.106 | -0.8473 |
| 1901 | -1.7974 | -3.8545 | -5.5038 | -6.0556 | -5.7021 | -5.4626 | -5.2854 | -5.0349 | -4.7637 | -4.5196 | -4.2742 | -4.0059 | -3.6574 | -3.3706 | -2.9474 | -2.5968 | -2.2023 | -1.7686 | -1.487 | -1.2241 | -0.9948 |
| 1902 | -1.9153 | -3.8893 | -5.4959 | -6.0861 | -5.7431 | -5.4805 | -5.2902 | -5.065 | -4.7771 | -4.557 | -4.2885 | -4.0266 | -3.6722 | -3.3828 | -2.9695 | -2.5899 | -2.2136 | -1.7739 | -1.4874 | -1.2219 | -0.9909 |
| 1903 | -1.9386 | -3.9822 | -5.6281 | -6.1741 | -5.8182 | -5.5785 | -5.3567 | -5.1332 | -4.8467 | -4.6384 | -4.347 | -4.082 | -3.7371 | -3.4324 | -3.0306 | -2.6245 | -2.2679 | -1.8338 | -1.5547 | -1.2998 | -1.0869 |
| 1904 | -1.8411 | -3.8859 | -5.6007 | -6.143 | -5.786 | -5.5592 | -5.3642 | -5.158 | -4.8584 | -4.6494 | -4.3469 | -4.0724 | -3.7069 | -3.3841 | -2.9965 | -2.5712 | -2.2025 | -1.7644 | -1.4704 | -1.1982 | -0.9808 |
| 1905 | -1.9746 | -4.0158 | -5.6368 | -6.1539 | -5.8083 | -5.5707 | -5.3876 | -5.1916 | -4.9003 | -4.6775 | -4.3766 | -4.0943 | -3.7435 | -3.406 | -3.0302 | -2.5994 | -2.2324 | -1.8044 | -1.4963 | -1.18 | -0.8864 |
| 1906 | -1.9339 | -4.0273 | -5.6117 | -6.139 | -5.7969 | -5.5866 | -5.4071 | -5.191 | -4.9147 | -4.665 | -4.3986 | -4.0863 | -3.7494 | -3.3914 | -3.0425 | -2.61 | -2.2158 | -1.7899 | -1.461 | -1.1123 | -0.792 |
| 1907 | -2.0688 | -4.0224 | -5.6472 | -6.179 | -5.821 | -5.604 | -5.4267 | -5.1951 | -4.9391 | -4.6512 | -4.4131 | -4.0765 | -3.7489 | -3.362 | -3.0131 | -2.5892 | -2.1804 | -1.7768 | -1.4525 | -1.0826 | -0.726 |
| 1908 | -2.0276 | -4.1031 | -5.6888 | -6.202 | -5.8638 | -5.6109 | -5.4468 | -5.2307 | -5.0025 | -4.6947 | -4.453 | -4.1042 | -3.7828 | -3.3908 | -3.0362 | -2.6261 | -2.1897 | -1.7841 | -1.4753 | -1.1048 | -0.7454 |
| 1909 | -2.1503 | -4.1112 | -5.6753 | -6.1778 | -5.8368 | -5.6239 | -5.4636 | -5.2393 | -5.0206 | -4.698 | -4.4534 | -4.098 | -3.7924 | -3.3682 | -2.9919 | -2.5852 | -2.1589 | -1.752 | -1.4327 | -1.0496 | -0.5983 |
| 1910 | -2.166 | -4.2274 | -5.7948 | -6.2564 | -5.923 | -5.685 | -5.5528 | -5.3099 | -5.0591 | -4.806 | -4.5267 | -4.1866 | -3.8529 | -3.4618 | -3.1003 | -2.6558 | -2.2441 | -1.8827 | -1.4861 | -1.2006 | -0.9066 |
| 1911 | -1.9517 | -4.0293 | -5.6766 | -6.1848 | -5.8476 | -5.6453 | -5.4992 | -5.2882 | -5.0422 | -4.7922 | -4.4997 | -4.1802 | -3.8404 | -3.454 | -3.0979 | -2.623 | -2.238 | -1.8553 | -1.4686 | -1.2143 | -0.9149 |
| 1912 | -2.2861 | -4.2258 | -5.7773 | -6.2577 | -5.8818 | -5.6951 | -5.5325 | -5.3342 | -5.0582 | -4.8349 | -4.5023 | -4.2061 | -3.846 | -3.4679 | -3.1051 | -2.6112 | -2.2325 | -1.8504 | -1.4572 | -1.1912 | -0.804 |
| 1913 | -2.1563 | -4.1987 | -5.7523 | -6.2389 | -5.9243 | -5.7007 | -5.5516 | -5.3379 | -5.0666 | -4.8329 | -4.5003 | -4.1939 | -3.8462 | -3.458 | -3.1125 | -2.6229 | -2.2504 | -1.8621 | -1.4803 | -1.1924 | -0.9316 |
| 1914 | -2.1938 | -4.178 | -5.6799 | -6.1561 | -5.2533 | -4.9328 | -5.0651 | -5.1163 | -4.9604 | -4.785 | -4.5006 | -4.1548 | -3.8497 | -3.4491 | -3.1023 | -2.6112 | -2.2382 | -1.8567 | -1.4599 | -1.1432 | -0.8304 |
| 1915 | -2.1922 | -3.9873 | -5.5582 | -6.059 | -4.8576 | -4.3181 | -4.5523 | -4.803 | -4.7984 | -4.7095 | -4.4628 | -4.1226 | -3.7926 | -3.3743 | -3.028 | -2.5112 | -2.1041 | -1.7227 | -1.3124 | -1.0356 | -0.6694 |
| 1916 | -2.3518 | -4.355 | -5.7247 | -6.1159 | -4.5687 | -3.8934 | -4.1373 | -4.5164 | -4.6802 | -4.7056 | -4.5372 | -4.1958 | -3.87 | -3.4674 | -3.0614 | -2.5794 | -2.1384 | -1.7589 | -1.3351 | -1.046 | -0.6978 |
| 1917 | -2.3689 | -4.2776 | -5.7261 | -6.1207 | -4.3932 | -3.6824 | -3.8896 | -4.2892 | -4.544 | -4.6485 | -4.5476 | -4.2428 | -3.8966 | -3.4938 | -3.0879 | -2.6189 | -2.1547 | -1.8005 | -1.3693 | -1.0708 | -0.6983 |
| 1918 | -2.2767 | -3.8421 | -5.1661 | -5.5892 | -4.2805 | -3.5275 | -3.5793 | -3.8976 | -4.2475 | -4.421 | -4.3587 | -4.1078 | -3.8661 | -3.4911 | -3.0841 | -2.6731 | -2.248 | -1.9308 | -1.5193 | -1.2542 | -0.8804 |
| 1919 | -2.337 | -4.3942 | -5.6405 | -6.0796 | -5.6065 | -5.2667 | -5.0299 | -5.0043 | -4.9821 | -4.8519 | -4.6073 | -4.2838 | -3.9356 | -3.5374 | -3.108 | -2.6651 | -2.1596 | -1.8082 | -1.3702 | -1.0722 | -0.7213 |
| 1920 | -2.3141 | -4.4339 | -5.7175 | -6.2275 | -5.8568 | -5.6055 | -5.4843 | -5.3542 | -5.1811 | -4.9994 | -4.7309 | -4.3916 | -4.0532 | -3.6437 | -3.2233 | -2.7947 | -2.3238 | -1.9507 | -1.5457 | -1.256 | -0.9382 |
| 1921 | -2.4679 | -4.5608 | -5.8911 | -6.3219 | -5.8917 | -5.6905 | -5.5985 | -5.4767 | -5.256 | -5.0436 | -4.7696 | -4.4259 | -4.0592 | -3.6547 | -3.2281 | -2.7692 | -2.311 | -1.9066 | -1.4843 | -1.189 | -0.8655 |
| 1922 | -2.545 | -4.3817 | -5.959 | -6.3252 | -5.9429 | -5.6718 | -5.5726 | -5.4358 | -5.2061 | -5.012 | -4.7185 | -4.3755 | -4.0011 | -3.5767 | -3.1359 | -2.6714 | -2.2105 | -1.8218 | -1.4268 | -1.1196 | -0.7616 |
| 1923 | -2.6342 | -4.6991 | -6.0957 | -6.414 | -5.9808 | -5.7591 | -5.6638 | -5.5578 | -5.3276 | -5.0915 | -4.7828 | -4.4673 | -4.0771 | -3.6597 | -3.2203 | -2.7725 | -2.3157 | -1.9093 | -1.4776 | -1.2212 | -0.883 |
| 1924 | -2.5599 | -4.618 | -6.0978 | -6.3957 | -5.974 | -5.7292 | -5.6648 | -5.5401 | -5.2928 | -5.0616 | -4.758 | -4.4399 | -4.0468 | -3.6182 | -3.1675 | -2.6986 | -2.2489 | -1.8515 | -1.4588 | -1.1405 | -0.8163 |
| 1925 | -2.5535 | -4.6346 | -6.0111 | -6.3933 | -5.955 | -5.7618 | -5.6669 | -5.5782 | -5.3459 | -5.0825 | -4.7629 | -4.4418 | -4.0713 | -3.6579 | -3.1892 | -2.7254 | -2.246 | -1.8525 | -1.43 | -1.1208 | -0.769 |
| 1926 | -2.6189 | -4.7804 | -6.0354 | -6.5049 | -6.0172 | -5.8095 | -5.7048 | -5.6351 | -5.3758 | -5.1228 | -4.8182 | -4.4891 | -4.1108 | -3.6983 | -3.2278 | -2.7748 | -2.2992 | -1.9055 | -1.4751 | -1.1789 | -0.8564 |
| 1927 | -2.6473 | -4.6901 | -6.0612 | -6.4635 | -5.998 | -5.7726 | -5.6865 | -5.5815 | -5.3288 | -5.0463 | -4.7572 | -4.4177 | -4.07 | -3.6347 | -3.1764 | -2.7004 | -2.2117 | -1.8226 | -1.4019 | -1.1247 | -0.8323 |
| 1928 | -2.6826 | -4.8631 | -6.0586 | -6.4322 | -5.9944 | -5.7891 | -5.7362 | -5.6189 | -5.4139 | -5.1191 | -4.8291 | -4.4724 | -4.1142 | -3.6986 | -3.2291 | -2.771 | -2.2976 | -1.9083 | -1.4871 | -1.1771 | -0.8658 |
| 1929 | -2.5642 | -4.5388 | -5.9829 | -6.4008 | -5.9492 | -5.7218 | -5.6807 | -5.5488 | -5.3159 | -5.0247 | -4.7169 | -4.3527 | -4.0094 | -3.573 | -3.1087 | -2.6231 | -2.1259 | -1.7508 | -1.3258 | -1.0362 | -0.6665 |
| 1930 | -2.7578 | -4.9779 | -6.0812 | -6.4752 | -6.0095 | -5.8112 | -5.7518 | -5.6418 | -5.4536 | -5.1775 | -4.8515 | -4.4949 | -4.1317 | -3.7109 | -3.2679 | -2.7933 | -2.3327 | -1.9521 | -1.5445 | -1.2267 | -0.8599 |
| 1931 | -2.6758 | -4.8862 | -6.1477 | -6.5228 | -5.9925 | -5.7767 | -5.7381 | -5.6521 | -5.4293 | -5.1478 | -4.8106 | -4.4644 | -4.0934 | -3.6705 | -3.2051 | -2.7289 | -2.245 | -1.842 | -1.4123 | -1.1134 | -0.8112 |
| 1932 | -2.7087 | -4.9652 | -6.182 | -6.581 | -6.0321 | -5.8009 | -5.7842 | -5.6949 | -5.4633 | -5.226 | -4.8549 | -4.5139 | -4.1211 | -3.6967 | -3.2265 | -2.7455 | -2.2633 | -1.8616 | -1.4183 | -1.1125 | -0.7365 |
| 1933 | -2.7569 | -5.0223 | -6.1221 | -6.5463 | -6.0266 | -5.7819 | -5.7413 | -5.6589 | -5.4008 | -5.1473 | -4.7886 | -4.4603 | -4.0925 | -3.6929 | -3.2375 | -2.7435 | -2.2628 | -1.8279 | -1.4058 | -1.0866 | -0.777 |
| 1934 | -2.7854 | -5.0211 | -6.0191 | -6.532 | -6.1094 | -5.8606 | -5.8238 | -5.7253 | -5.5126 | -5.263 | -4.8852 | -4.5168 | -4.1384 | -3.7166 | -3.2701 | -2.779 | -2.3298 | -1.9342 | -1.5138 | -1.2238 | -0.8869 |
| 1935 | -2.8118 | -5.2861 | -6.1942 | -6.6324 | -6.1845 | -5.9025 | -5.852 | -5.7727 | -5.5399 | -5.2806 | -4.9078 | -4.5375 | -4.1545 | -3.7165 | -3.2717 | -2.7925 | -2.3187 | -1.9117 | -1.4988 | -1.1662 | -0.845 |
| 1936 | -2.7829 | -5.2075 | -6.2201 | -6.719 | -6.2385 | -5.916 | -5.9067 | -5.8327 | -5.5624 | -5.3011 | -4.9215 | -4.5073 | -4.1274 | -3.692 | -3.2555 | -2.7657 | -2.2826 | -1.8807 | -1.4622 | -1.1122 | -0.7684 |
| 1937 | -2.8033 | -5.2803 | -6.2818 | -6.7452 | -6.2289 | -5.9227 | -5.8969 | -5.7942 | -5.5582 | -5.2666 | -4.906 | -4.4922 | -4.1254 | -3.6531 | -3.2427 | -2.7601 | -2.2782 | -1.8576 | -1.4385 | -1.0869 | -0.7349 |
| 1938 | -2.8934 | -5.3875 | -6.282 | -6.7398 | -6.2812 | -5.9892 | -5.9699 | -5.8922 | -5.6519 | -5.3685 | -4.9908 | -4.5803 | -4.1985 | -3.7432 | -3.3118 | -2.8413 | -2.3491 | -1.9494 | -1.5347 | -1.1964 | -0.8936 |
| 1939 | -2.9514 | -5.6552 | -6.5153 | -6.883 | -6.3171 | -6.0068 | -5.9669 | -5.9182 | -5.6867 | -5.3839 | -4.9927 | -4.5563 | -4.16 | -3.713 | -3.2807 | -2.7934 | -2.2843 | -1.8659 | -1.4481 | -1.1046 | -0.7145 |
| 1940 | -2.8494 | -5.3285 | -6.2333 | -6.5729 | -5.787 | -5.2562 | -5.4771 | -5.5357 | -5.4069 | -5.1743 | -4.8204 | -4.4023 | -4.008 | -3.5853 | -3.1671 | -2.7077 | -2.2031 | -1.7843 | -1.3609 | -1.0271 | -0.6085 |
| 1941 | -2.8064 | -5.2374 | -6.1894 | -6.5937 | -5.8582 | -5.4714 | -5.6063 | -5.6107 | -5.4953 | -5.2539 | -4.9203 | -4.5354 | -4.1323 | -3.7218 | -3.2806 | -2.8334 | -2.3326 | -1.9121 | -1.4691 | -1.1367 | -0.7403 |
| 1942 | -2.9155 | -5.6781 | -6.5065 | -6.8669 | -5.717 | -5.2196 | -5.4179 | -5.5461 | -5.5534 | -5.3866 | -5.0423 | -4.6688 | -4.2425 | -3.8302 | -3.3674 | -2.9288 | -2.4398 | -2.0229 | -1.5803 | -1.2559 | -0.871 |
| 1943 | -2.9589 | -5.708 | -6.5715 | -6.8702 | -5.4788 | -5.0439 | -5.2249 | -5.417 | -5.5128 | -5.3585 | -5.0392 | -4.6293 | -4.2313 | -3.8206 | -3.3607 | -2.9023 | -2.41 | -1.9664 | -1.5064 | -1.1638 | -0.805 |
| 1944 | -3.0215 | -5.8697 | -6.5851 | -6.8582 | -5.3334 | -4.8954 | -5.1362 | -5.4118 | -5.564 | -5.3999 | -5.0754 | -4.6757 | -4.2714 | -3.8288 | -3.3895 | -2.9452 | -2.4753 | -2.027 | -1.5837 | -1.2488 | -0.8463 |
| 1945 | -3.0792 | -5.9389 | -6.7362 | -6.9975 | -5.2696 | -4.5699 | -4.8336 | -5.2043 | -5.4361 | -5.4117 | -5.1127 | -4.7027 | -4.287 | -3.8368 | -3.401 | -2.9405 | -2.4683 | -2.0239 | -1.5928 | -1.2372 | -0.9141 |
| 1946 | -3.0785 | -6.172 | -7.0613 | -7.189 | -6.5609 | -6.2974 | -6.3063 | -6.181 | -5.9682 | -5.6163 | -5.1429 | -4.735 | -4.3022 | -3.841 | -3.4244 | -2.9393 | -2.4502 | -2.0058 | -1.5632 | -1.1973 | -0.8145 |
| 1947 | -3.0831 | -6.1454 | -7.0187 | -7.2635 | -6.6163 | -6.3289 | -6.2704 | -6.1766 | -5.9758 | -5.6284 | -5.1598 | -4.7238 | -4.2937 | -3.8317 | -3.4008 | -2.8959 | -2.404 | -1.953 | -1.507 | -1.1558 | -0.7864 |
| 1948 | -3.4006 | -6.3401 | -7.1953 | -7.4232 | -6.7624 | -6.4688 | -6.363 | -6.2643 | -6.0804 | -5.7153 | -5.2301 | -4.8013 | -4.3571 | -3.8883 | -3.4669 | -2.9902 | -2.5242 | -2.0989 | -1.6808 | -1.3445 | -0.9489 |
| 1949 | -3.4402 | -6.4573 | -7.2837 | -7.4809 | -6.8553 | -6.5004 | -6.4179 | -6.3387 | -6.0765 | -5.7155 | -5.2242 | -4.779 | -4.3143 | -3.8376 | -3.3919 | -2.8933 | -2.4201 | -1.982 | -1.5307 | -1.1769 | -0.7972 |
| 1950 | -3.5119 | -6.6056 | -7.3542 | -7.6317 | -6.9927 | -6.6784 | -6.5123 | -6.3922 | -6.1365 | -5.7714 | -5.2413 | -4.7907 | -4.332 | -3.8476 | -3.3943 | -2.9141 | -2.4116 | -1.9709 | -1.5252 | -1.1694 | -0.8498 |
| 1951 | -3.4967 | -6.5814 | -7.5165 | -7.6598 | -7.1845 | -6.7908 | -6.6306 | -6.4406 | -6.1573 | -5.7659 | -5.2437 | -4.7444 | -4.2771 | -3.7839 | -3.3106 | -2.837 | -2.3291 | -1.8818 | -1.4441 | -1.0996 | -0.77 |
| 1952 | -3.5718 | -6.7416 | -7.6142 | -7.7712 | -7.2764 | -6.874 | -6.7861 | -6.5817 | -6.2513 | -5.8487 | -5.3305 | -4.8269 | -4.3416 | -3.8882 | -3.4222 | -2.957 | -2.4614 | -2.015 | -1.5738 | -1.2251 | -0.8629 |
| 1953 | -3.5928 | -6.7426 | -7.6294 | -7.8229 | -7.3839 | -6.9824 | -6.826 | -6.6186 | -6.2879 | -5.8837 | -5.3505 | -4.8432 | -4.3648 | -3.8879 | -3.4243 | -2.9555 | -2.4609 | -2.0128 | -1.5712 | -1.237 | -0.8609 |
| 1954 | -3.6588 | -6.9667 | -7.8054 | -7.9037 | -7.399 | -7.0484 | -6.9068 | -6.6386 | -6.3267 | -5.8774 | -5.3792 | -4.8478 | -4.3789 | -3.9067 | -3.4401 | -2.9651 | -2.4867 | -2.0279 | -1.5961 | -1.2259 | -0.8571 |
| 1955 | -3.6806 | -6.9044 | -7.7591 | -7.8818 | -7.384 | -7.0648 | -6.9352 | -6.7195 | -6.3889 | -5.9158 | -5.3874 | -4.853 | -4.381 | -3.9037 | -3.4285 | -2.9461 | -2.4538 | -1.9907 | -1.5375 | -1.1928 | -0.793 |
| 1956 | -3.7044 | -7.006 | -7.8216 | -8.011 | -7.5014 | -7.1426 | -7.0046 | -6.7524 | -6.3935 | -5.9259 | -5.4038 | -4.8933 | -4.3799 | -3.9043 | -3.4382 | -2.9521 | -2.4573 | -2.0063 | -1.5393 | -1.1887 | -0.8299 |
| 1957 | -3.7343 | -6.9387 | -7.8019 | -7.8922 | -7.3236 | -7.1041 | -6.9965 | -6.7754 | -6.3781 | -5.9134 | -5.411 | -4.8762 | -4.367 | -3.894 | -3.4419 | -2.9741 | -2.5158 | -2.0731 | -1.6376 | -1.2695 | -0.9074 |
| 1958 | -3.7652 | -7.0367 | -7.8214 | -8.0635 | -7.4609 | -7.1514 | -7.0558 | -6.8116 | -6.4284 | -5.9375 | -5.4257 | -4.8922 | -4.3812 | -3.9182 | -3.4506 | -2.9735 | -2.4905 | -2.0362 | -1.5874 | -1.219 | -0.8552 |
| 1959 | -3.7875 | -7.0113 | -7.8019 | -8.0039 | -7.3581 | -7.1132 | -7.0862 | -6.8344 | -6.3966 | -5.9666 | -5.4603 | -4.9129 | -4.3848 | -3.9187 | -3.4671 | -2.984 | -2.5015 | -2.0636 | -1.6087 | -1.2502 | -0.865 |
| 1960 | -3.7885 | -7.0512 | -7.7384 | -8.0423 | -7.3869 | -7.1297 | -7.1164 | -6.8762 | -6.4182 | -5.98 | -5.4451 | -4.9294 | -4.4117 | -3.9304 | -3.4825 | -3.0178 | -2.5189 | -2.0851 | -1.6385 | -1.2663 | -0.9185 |
| 1961 | -3.8086 | -6.9902 | -7.8182 | -8.0278 | -7.3443 | -7.1215 | -7.114 | -6.845 | -6.429 | -5.9655 | -5.4273 | -4.9141 | -4.3985 | -3.898 | -3.4445 | -2.9701 | -2.4913 | -2.0512 | -1.603 | -1.2222 | -0.8277 |
| 1962 | -3.7953 | -7.0633 | -7.8697 | -7.9959 | -7.3436 | -7.1356 | -7.1425 | -6.8616 | -6.4214 | -5.9751 | -5.4258 | -4.9248 | -4.3932 | -3.8921 | -3.4457 | -2.976 | -2.5065 | -2.0556 | -1.5991 | -1.2286 | -0.872 |
| 1963 | -3.8295 | -7.0071 | -7.8173 | -8.0625 | -7.3642 | -7.1618 | -7.1251 | -6.8506 | -6.4366 | -5.9417 | -5.3994 | -4.9173 | -4.3869 | -3.8833 | -3.4332 | -2.9623 | -2.4974 | -2.0299 | -1.5771 | -1.211 | -0.8614 |
| 1964 | -3.8769 | -7.1223 | -7.8538 | -8.0265 | -7.2626 | -7.1492 | -7.118 | -6.8826 | -6.4611 | -5.9246 | -5.4434 | -4.94 | -4.4381 | -3.9369 | -3.5041 | -3.0469 | -2.6147 | -2.1451 | -1.7148 | -1.3707 | -0.986 |
| 1965 | -3.9422 | -7.1051 | -7.8413 | -7.9528 | -7.251 | -7.1863 | -7.1315 | -6.9134 | -6.4438 | -5.9276 | -5.4474 | -4.9255 | -4.4411 | -3.9297 | -3.4834 | -3.0332 | -2.5983 | -2.1379 | -1.6982 | -1.3271 | -0.9716 |
| 1966 | -3.949 | -7.0799 | -7.9089 | -8.0002 | -7.1975 | -7.1992 | -7.1603 | -6.9038 | -6.4781 | -5.9565 | -5.4461 | -4.9149 | -4.4338 | -3.9358 | -3.4698 | -3.0233 | -2.5703 | -2.1169 | -1.6783 | -1.2978 | -0.9314 |
| 1967 | -3.9892 | -7.1664 | -7.9047 | -7.9716 | -7.2727 | -7.2552 | -7.2115 | -6.9852 | -6.5191 | -5.9898 | -5.4746 | -4.9603 | -4.4653 | -3.9756 | -3.5104 | -3.0703 | -2.6314 | -2.1829 | -1.7473 | -1.3615 | -0.9944 |
| 1968 | -3.9912 | -7.1231 | -7.8942 | -8.023 | -7.3665 | -7.3038 | -7.2487 | -6.9992 | -6.5436 | -5.9689 | -5.4588 | -4.9267 | -4.4433 | -3.95 | -3.4774 | -3.0222 | -2.561 | -2.1158 | -1.6657 | -1.2765 | -0.9014 |
| 1969 | -4.012 | -7.1615 | -7.9946 | -8.1318 | -7.3305 | -7.2903 | -7.2239 | -6.9777 | -6.5464 | -5.9396 | -5.3809 | -4.919 | -4.4254 | -3.9246 | -3.4409 | -3.01 | -2.5832 | -2.1587 | -1.7341 | -1.3487 | -0.9583 |
| 1970 | -4.0021 | -7.239 | -7.9989 | -8.123 | -7.3633 | -7.243 | -7.2529 | -6.9964 | -6.5809 | -5.9779 | -5.4229 | -4.9397 | -4.4405 | -3.964 | -3.4795 | -3.0393 | -2.6019 | -2.1692 | -1.7385 | -1.3457 | -0.9448 |
| 1971 | -4.0244 | -7.2729 | -7.9148 | -8.098 | -7.3426 | -7.2831 | -7.3042 | -6.9941 | -6.5743 | -5.997 | -5.4293 | -4.9562 | -4.4737 | -3.9932 | -3.5295 | -3.0788 | -2.6335 | -2.1878 | -1.7542 | -1.3561 | -0.9796 |
| 1972 | -4.0762 | -7.2076 | -7.9582 | -8.1717 | -7.3651 | -7.2582 | -7.285 | -7.0584 | -6.5695 | -6.0157 | -5.4205 | -4.9276 | -4.4391 | -3.9735 | -3.4956 | -3.0329 | -2.5933 | -2.157 | -1.7177 | -1.3256 | -0.9403 |
| 1973 | -4.1006 | -7.2781 | -8.0279 | -8.189 | -7.3546 | -7.2125 | -7.24 | -7.0392 | -6.6118 | -6.0132 | -5.4251 | -4.9506 | -4.4498 | -4.005 | -3.5193 | -3.0586 | -2.6131 | -2.1623 | -1.7274 | -1.3329 | -0.9327 |
| 1974 | -4.1219 | -7.3309 | -8.0959 | -8.1945 | -7.3632 | -7.2847 | -7.3332 | -7.0598 | -6.6268 | -6.0396 | -5.4477 | -4.9154 | -4.4797 | -4.0135 | -3.5339 | -3.0612 | -2.6388 | -2.1827 | -1.7419 | -1.3234 | -0.9475 |
| 1975 | -4.1678 | -7.4074 | -8.1509 | -8.2556 | -7.3866 | -7.2528 | -7.3055 | -7.0735 | -6.6466 | -6.0777 | -5.4826 | -4.9488 | -4.5079 | -4.0192 | -3.552 | -3.0872 | -2.6437 | -2.1877 | -1.7506 | -1.3428 | -0.9467 |
| 1976 | -4.2531 | -7.4964 | -8.1449 | -8.2564 | -7.3852 | -7.2848 | -7.3052 | -7.0983 | -6.6469 | -6.091 | -5.5074 | -4.9479 | -4.5004 | -4.0019 | -3.5456 | -3.0762 | -2.6229 | -2.163 | -1.7097 | -1.2943 | -0.9014 |
| 1977 | -4.2836 | -7.4995 | -8.234 | -8.3221 | -7.4333 | -7.3083 | -7.3231 | -7.129 | -6.6697 | -6.1433 | -5.5281 | -4.9872 | -4.5305 | -4.0349 | -3.5791 | -3.1196 | -2.6729 | -2.2243 | -1.7858 | -1.3765 | -0.9778 |
| 1978 | -4.2968 | -7.4802 | -8.1665 | -8.2706 | -7.3619 | -7.2504 | -7.2799 | -7.1019 | -6.6332 | -6.1386 | -5.5441 | -4.9676 | -4.5103 | -4.0291 | -3.5733 | -3.1188 | -2.6653 | -2.2256 | -1.7851 | -1.3841 | -0.9822 |
| 1979 | -4.3143 | -7.5968 | -8.2016 | -8.3066 | -7.4374 | -7.3475 | -7.2828 | -7.1065 | -6.6952 | -6.1536 | -5.5623 | -4.9838 | -4.4814 | -4.0406 | -3.5883 | -3.1218 | -2.6599 | -2.2198 | -1.7824 | -1.3621 | -0.9743 |
| 1980 | -4.3842 | -7.5823 | -8.2684 | -8.3655 | -7.4321 | -7.3621 | -7.3442 | -7.1619 | -6.7223 | -6.1943 | -5.6132 | -5.0359 | -4.5177 | -4.0651 | -3.6133 | -3.1541 | -2.6959 | -2.2574 | -1.8096 | -1.4006 | -1.0096 |
| 1981 | -4.5009 | -7.6074 | -8.3607 | -8.3234 | -7.4558 | -7.429 | -7.3609 | -7.1567 | -6.7979 | -6.2069 | -5.6351 | -5.069 | -4.5422 | -4.1028 | -3.6358 | -3.1679 | -2.7208 | -2.2591 | -1.8244 | -1.4097 | -1.0041 |
| 1982 | -4.5244 | -7.6702 | -8.4612 | -8.3447 | -7.5137 | -7.3996 | -7.3799 | -7.1439 | -6.7945 | -6.2576 | -5.6828 | -5.106 | -4.5598 | -4.1076 | -3.628 | -3.1706 | -2.7221 | -2.2637 | -1.8215 | -1.4115 | -1.0195 |
| 1983 | -4.5807 | -7.7286 | -8.4039 | -8.3727 | -7.528 | -7.4728 | -7.3825 | -7.1827 | -6.8042 | -6.2873 | -5.6877 | -5.1391 | -4.5841 | -4.101 | -3.6344 | -3.1883 | -2.7421 | -2.2789 | -1.8397 | -1.4222 | -1.0255 |
| 1984 | -4.6473 | -7.7623 | -8.4788 | -8.3857 | -7.5813 | -7.4494 | -7.3777 | -7.1942 | -6.8368 | -6.3271 | -5.7229 | -5.1726 | -4.6151 | -4.1013 | -3.6784 | -3.2217 | -2.7773 | -2.3225 | -1.8902 | -1.4599 | -1.0573 |
| 1985 | -4.653 | -7.6996 | -8.524 | -8.3323 | -7.6322 | -7.4623 | -7.4681 | -7.2039 | -6.8126 | -6.309 | -5.7464 | -5.1835 | -4.6265 | -4.0986 | -3.6708 | -3.1963 | -2.7426 | -2.2791 | -1.8347 | -1.4017 | -1.0096 |
| 1986 | -4.6434 | -7.7717 | -8.5698 | -8.5026 | -7.5755 | -7.4503 | -7.4332 | -7.1774 | -6.8186 | -6.3438 | -5.7581 | -5.2241 | -4.6629 | -4.1295 | -3.6957 | -3.2182 | -2.7649 | -2.3165 | -1.868 | -1.4433 | -1.0457 |
| 1987 | -4.6671 | -7.7817 | -8.6401 | -8.4595 | -7.592 | -7.4374 | -7.4505 | -7.1316 | -6.8321 | -6.3535 | -5.7939 | -5.253 | -4.6842 | -4.1595 | -3.723 | -3.2443 | -2.8067 | -2.3599 | -1.9264 | -1.4982 | -1.088 |
| 1988 | -4.6844 | -7.7816 | -8.5526 | -8.4763 | -7.6114 | -7.4275 | -7.4397 | -7.1379 | -6.8232 | -6.357 | -5.8045 | -5.2873 | -4.7291 | -4.1699 | -3.7196 | -3.2503 | -2.8185 | -2.3664 | -1.9154 | -1.4898 | -1.0549 |
| 1989 | -4.7661 | -7.8061 | -8.5509 | -8.5661 | -7.5555 | -7.4198 | -7.4172 | -7.1925 | -6.7923 | -6.388 | -5.8393 | -5.317 | -4.7608 | -4.2063 | -3.7089 | -3.2824 | -2.8173 | -2.3578 | -1.8993 | -1.4627 | -1.0336 |
| 1990 | -4.8158 | -7.8682 | -8.6577 | -8.5682 | -7.5638 | -7.3714 | -7.3279 | -7.1887 | -6.7943 | -6.3825 | -5.8624 | -5.3363 | -4.7841 | -4.2345 | -3.7394 | -3.3134 | -2.8481 | -2.3984 | -1.9517 | -1.5194 | -1.0572 |
| 1991 | -4.9017 | -7.9127 | -8.6028 | -8.5728 | -7.5739 | -7.3932 | -7.3873 | -7.1701 | -6.7949 | -6.387 | -5.8911 | -5.347 | -4.8311 | -4.2732 | -3.756 | -3.3201 | -2.8486 | -2.3939 | -1.9406 | -1.4928 | -1.0518 |
| 1992 | -5.0219 | -8.049 | -8.7471 | -8.6937 | -7.7016 | -7.4431 | -7.3968 | -7.1682 | -6.7891 | -6.3975 | -5.9286 | -5.3866 | -4.8615 | -4.3037 | -3.7869 | -3.3448 | -2.8724 | -2.4278 | -1.9734 | -1.5443 | -1.0968 |
| 1993 | -5.0695 | -8.04 | -8.8555 | -8.5918 | -7.7383 | -7.4432 | -7.3738 | -7.1581 | -6.8303 | -6.394 | -5.9453 | -5.3795 | -4.8684 | -4.3108 | -3.783 | -3.3207 | -2.8506 | -2.3971 | -1.9233 | -1.4718 | -1.013 |
| 1994 | -5.0817 | -8.1417 | -8.8799 | -8.6905 | -7.814 | -7.4482 | -7.3633 | -7.1097 | -6.8331 | -6.3832 | -5.9696 | -5.4379 | -4.9305 | -4.3759 | -3.8383 | -3.345 | -2.9245 | -2.4476 | -1.9937 | -1.5497 | -1.088 |
| 1995 | -5.0959 | -8.2279 | -8.891 | -8.6679 | -7.7491 | -7.4331 | -7.3394 | -7.1167 | -6.8267 | -6.3817 | -5.9387 | -5.4325 | -4.924 | -4.392 | -3.846 | -3.3493 | -2.9049 | -2.4234 | -1.9644 | -1.4905 | -1.0334 |
| 1996 | -5.0901 | -8.162 | -9.0245 | -8.7973 | -7.7186 | -7.4494 | -7.3248 | -7.1247 | -6.8335 | -6.4025 | -5.9522 | -5.4716 | -4.9432 | -4.4289 | -3.892 | -3.3797 | -2.9442 | -2.4426 | -1.9812 | -1.5216 | -1.0536 |
| 1997 | -5.1299 | -8.2143 | -8.9524 | -8.7176 | -7.7247 | -7.3982 | -7.3584 | -7.1687 | -6.8602 | -6.4236 | -5.9768 | -5.4886 | -4.9733 | -4.468 | -3.9246 | -3.4055 | -2.9648 | -2.4547 | -1.9901 | -1.5223 | -1.0648 |
| 1998 | -5.1653 | -8.1859 | -9.0133 | -8.8402 | -7.8085 | -7.4575 | -7.3242 | -7.1512 | -6.8642 | -6.4319 | -5.9794 | -5.5014 | -4.9811 | -4.4823 | -3.9543 | -3.4188 | -2.9636 | -2.4606 | -2.0023 | -1.5242 | -1.0628 |
| 1999 | -5.1469 | -8.2003 | -9.0841 | -8.8336 | -7.8118 | -7.4713 | -7.3591 | -7.1693 | -6.864 | -6.4445 | -5.9754 | -5.5178 | -5.0098 | -4.504 | -3.9803 | -3.4455 | -2.9455 | -2.4935 | -1.9956 | -1.5111 | -1.0431 |
| 2000 | -5.192 | -8.3825 | -9.1064 | -8.9007 | -7.8418 | -7.5128 | -7.3556 | -7.1678 | -6.8501 | -6.4599 | -5.9866 | -5.5308 | -5.0561 | -4.5458 | -4.0378 | -3.5077 | -3.0085 | -2.5444 | -2.0362 | -1.5666 | -1.0834 |
| 2001 | -5.2109 | -8.3543 | -9.0913 | -8.9189 | -7.852 | -7.5063 | -7.4292 | -7.1554 | -6.8841 | -6.4884 | -5.9971 | -5.5365 | -5.0853 | -4.577 | -4.0924 | -3.5531 | -3.0337 | -2.5685 | -2.0377 | -1.5819 | -1.0989 |
| 2002 | -5.2459 | -8.3992 | -9.1251 | -8.9027 | -7.9088 | -7.56 | -7.4224 | -7.1714 | -6.8991 | -6.4864 | -5.9842 | -5.5658 | -5.1044 | -4.5965 | -4.117 | -3.5788 | -3.0421 | -2.5769 | -2.022 | -1.5642 | -1.0961 |
| 2003 | -5.2111 | -8.3214 | -9.154 | -8.9711 | -7.9766 | -7.5669 | -7.4492 | -7.1995 | -6.9014 | -6.4759 | -6.0153 | -5.5551 | -5.1152 | -4.6096 | -4.1315 | -3.606 | -3.0606 | -2.5574 | -2.0126 | -1.5505 | -1.073 |
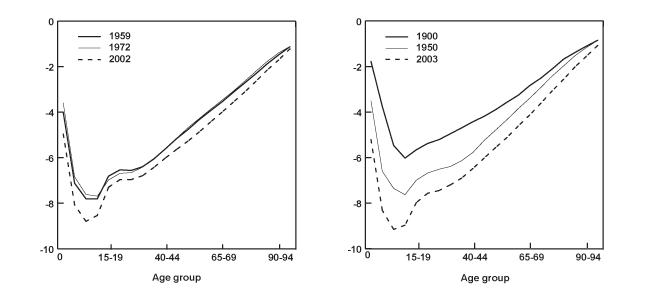
| Age group | United States | United Kingdom | ||||
|---|---|---|---|---|---|---|
| 1959 | 1972 | 2002 | 1900 | 1950 | 2003 | |
| 0 | -3.6015 | -4.017 | -4.9619 | -1.7791 | -3.5119 | -5.2111 |
| 1–4 | -6.8416 | -7.1213 | -8.073 | -3.7567 | -6.6056 | -8.3214 |
| 4–9 | -7.6136 | -7.8045 | -8.7967 | -5.4683 | -7.3542 | -9.154 |
| 10–14 | -7.6905 | -7.8134 | -8.5374 | -6.0237 | -7.6317 | -8.9711 |
| 15–19 | -6.9784 | -6.8078 | -7.2954 | -5.6575 | -6.9927 | -7.9766 |
| 20–24 | -6.6849 | -6.5349 | -6.963 | -5.379 | -6.6784 | -7.5669 |
| 25–29 | -6.6566 | -6.5589 | -6.9602 | -5.2118 | -6.5123 | -7.4492 |
| 30–34 | -6.4148 | -6.3952 | -6.7893 | -4.9542 | -6.3922 | -7.1995 |
| 35–39 | -6.0735 | -6.0484 | -6.4254 | -4.6949 | -6.1365 | -6.9014 |
| 40–44 | -5.6217 | -5.6145 | -6.0181 | -4.4234 | -5.7714 | -6.4759 |
| 45–49 | -5.1455 | -5.16 | -5.6339 | -4.1841 | -5.2413 | -6.0153 |
| 50–54 | -4.6819 | -4.7645 | -5.2728 | -3.894 | -4.7907 | -5.5551 |
| 55–59 | -4.2788 | -4.3261 | -4.8658 | -3.5666 | -4.332 | -5.1152 |
| 60–64 | -3.8687 | -3.9318 | -4.4287 | -3.2582 | -3.8476 | -4.6096 |
| 65–69 | -3.4745 | -3.5501 | -4.0016 | -2.8397 | -3.3943 | -4.1315 |
| 70–74 | -3.0754 | -3.1287 | -3.5606 | -2.5047 | -2.9141 | -3.606 |
| 75–79 | -2.644 | -2.7184 | -3.1163 | -2.1014 | -2.4116 | -3.0606 |
| 80–84 | -2.1996 | -2.3069 | -2.6435 | -1.6736 | -1.9709 | -2.5574 |
| 85–89 | -1.7665 | -1.8735 | -2.1448 | -1.3834 | -1.5252 | -2.0126 |
| 90–94 | -1.3965 | -1.483 | -1.7063 | -1.106 | -1.1694 | -1.5505 |
| 95 or older | -1.1108 | -1.1236 | -1.2167 | -0.8473 | -0.8498 | -1.073 |
When modeling mortality, some researchers treat unusual data spikes as outliers by introducing dummy variables to remove their influence. An alternative view is that these observations represent rare but nonetheless potentially recurring shocks, and thus, their exclusion is likely to underestimate true uncertainty. The analysis in this paper subscribes to the latter practice, treating all observations equally. Yet a third possibility, as Lee and Carter (2000) suggest, is to incorporate additional uncertainty in every forecast period due to such events. For example, this can be accomplished by introducing a chance of a shock to the mortality index kt the size of the 1918 influenza pandemic, where T denotes the sample size. Nevertheless, the authors report that this practice has a negligible effect in the resulting projections.
A second characteristic in the age profile of all-cause mortality is a downward trend. That is, while mortality across the age groups maintains its regular shape, it also shifts downward over time. This can be clearly seen in the bottom graphs of Chart 1, which show the logarithm of the age mortality profile at three different points in time for the same two countries. It is evident that the death rates among the various age groups tend to move together. Thus, it is not surprising that a third feature of all-cause mortality involves a high degree of cross-correlation among the rates for different ages.
Table 2 presents the sample correlation between each age series and its immediately adjacent group for all 16 countries. For instance, the top entry in the column of Table 2 corresponding to Austria indicates that the estimated correlation between the age 0 and age 1–4 groups is 0.988. Similarly, the correlation between age groups 90–94 and 95 or older is 0.748 (the last entry in the same column). Evidently, mortality across the ages shows a high degree of positive association. Finally, Table 3 shows the sample standard deviation of the mortality rates corresponding to several age groups. Clearly, there is much more variation in mortality within the older age groups (particularly for the last series age 95 or older), as well as before age 1. Typically, the standard deviation decreases rapidly from a relatively high value at birth (age 0), until it reaches the 10–14 age group. Then, it increases steadily from ages 15–19 to the last series (age 95 or older), where it often attains its highest value.
| Age Group |
Austria | Belgium | Canada | Denmark | Finland | France | Germany | Italy | Japan | Netherlands | Norway | Spain | Sweden | Switzerland | United Kingdom |
United States |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.988 | 0.969 | 0.986 | 0.903 | 0.962 | 0.980 | 0.994 | 0.963 | 0.943 | 0.968 | 0.963 | 0.940 | 0.928 | 0.987 | 0.957 | 0.990 |
| 1–4 | 0.977 | 0.979 | 0.992 | 0.988 | 0.990 | 0.986 | 0.951 | 0.979 | 0.971 | 0.984 | 0.990 | 0.984 | 0.970 | 0.994 | 0.982 | 0.991 |
| 5–9 | 0.985 | 0.988 | 0.996 | 0.981 | 0.954 | 0.992 | 0.996 | 0.974 | 0.993 | 0.989 | 0.951 | 0.990 | 0.973 | 0.985 | 0.995 | 0.994 |
| 10–14 | 0.894 | 0.985 | 0.989 | 0.973 | 0.854 | 0.798 | 0.913 | 0.977 | 0.988 | 0.982 | 0.957 | 0.993 | 0.963 | 0.981 | 0.885 | 0.804 |
| 15–19 | 0.925 | 0.932 | 0.996 | 0.980 | 0.845 | 0.942 | 0.944 | 0.994 | 0.994 | 0.992 | 0.991 | 0.990 | 0.982 | 0.986 | 0.963 | 0.978 |
| 20–24 | 0.983 | 0.992 | 0.995 | 0.993 | 0.973 | 0.990 | 0.979 | 0.996 | 0.999 | 0.994 | 0.995 | 0.991 | 0.989 | 0.996 | 0.981 | 0.938 |
| 25–29 | 0.974 | 0.983 | 0.996 | 0.993 | 0.982 | 0.986 | 0.979 | 0.999 | 0.997 | 0.997 | 0.988 | 0.995 | 0.989 | 0.994 | 0.960 | 0.867 |
| 30–34 | 0.963 | 0.991 | 0.997 | 0.992 | 0.988 | 0.968 | 0.984 | 0.990 | 0.996 | 0.997 | 0.987 | 0.986 | 0.985 | 0.990 | 0.976 | 0.935 |
| 35–39 | 0.968 | 0.994 | 0.989 | 0.993 | 0.975 | 0.958 | 0.964 | 0.994 | 0.997 | 0.998 | 0.993 | 0.993 | 0.987 | 0.994 | 0.991 | 0.945 |
| 40–44 | 0.966 | 0.990 | 0.980 | 0.993 | 0.982 | 0.978 | 0.967 | 0.987 | 0.994 | 0.997 | 0.989 | 0.984 | 0.994 | 0.994 | 0.993 | 0.981 |
| 45–49 | 0.956 | 0.982 | 0.984 | 0.992 | 0.984 | 0.991 | 0.955 | 0.982 | 0.994 | 0.997 | 0.986 | 0.990 | 0.994 | 0.996 | 0.992 | 0.988 |
| 50–54 | 0.964 | 0.984 | 0.994 | 0.993 | 0.985 | 0.996 | 0.964 | 0.969 | 0.994 | 0.996 | 0.986 | 0.976 | 0.993 | 0.997 | 0.989 | 0.993 |
| 55–59 | 0.978 | 0.991 | 0.993 | 0.992 | 0.989 | 0.997 | 0.973 | 0.955 | 0.995 | 0.997 | 0.986 | 0.975 | 0.993 | 0.997 | 0.982 | 0.991 |
| 60–64 | 0.984 | 0.996 | 0.989 | 0.985 | 0.986 | 0.998 | 0.977 | 0.964 | 0.997 | 0.995 | 0.986 | 0.982 | 0.976 | 0.996 | 0.984 | 0.996 |
| 65–69 | 0.990 | 0.996 | 0.995 | 0.985 | 0.990 | 0.998 | 0.986 | 0.931 | 0.994 | 0.994 | 0.984 | 0.980 | 0.989 | 0.996 | 0.980 | 0.994 |
| 70–74 | 0.990 | 0.995 | 0.995 | 0.970 | 0.990 | 0.998 | 0.992 | 0.931 | 0.993 | 0.993 | 0.965 | 0.963 | 0.979 | 0.992 | 0.982 | 0.991 |
| 75–79 | 0.996 | 0.993 | 0.995 | 0.973 | 0.985 | 0.997 | 0.996 | 0.929 | 0.996 | 0.989 | 0.871 | 0.966 | 0.963 | 0.994 | 0.983 | 0.997 |
| 80–84 | 0.992 | 0.992 | 0.995 | 0.963 | 0.953 | 0.997 | 0.996 | 0.945 | 0.996 | 0.985 | 0.921 | 0.961 | 0.923 | 0.990 | 0.968 | 0.997 |
| 85–89 | 0.978 | 0.980 | 0.975 | 0.839 | 0.750 | 0.992 | 0.994 | 0.937 | 0.996 | 0.953 | 0.801 | 0.849 | 0.842 | 0.955 | 0.977 | 0.994 |
| 90–94 | 0.748 | 0.885 | 0.913 | 0.699 | 0.646 | 0.980 | 0.986 | 0.890 | 0.978 | 0.793 | 0.646 | 0.877 | 0.639 | 0.777 | 0.918 | 0.881 |
| SOURCE: Author's calculations. | ||||||||||||||||
| Country | Age 0 | Age 5-9 | Age 15-19 | Age 30-34 | Age 55-59 | Age 75-79 | Age 85-89 | Age 95 or older |
|---|---|---|---|---|---|---|---|---|
| Austria | 0.02176 | 0.00028 | 0.00028 | 0.00051 | 0.00223 | 0.01625 | 0.03080 | 0.03933 |
| Belgium | 0.03248 | 0.00072 | 0.00085 | 0.00132 | 0.00334 | 0.01863 | 0.03786 | 0.06341 |
| Canada | 0.03574 | 0.00079 | 0.00076 | 0.00117 | 0.00286 | 0.01662 | 0.03134 | 0.03085 |
| Denmark | 0.06913 | 0.00400 | 0.00217 | 0.00314 | 0.00584 | 0.02108 | 0.04059 | 0.08381 |
| Finland | 0.06111 | 0.00387 | 0.00290 | 0.00416 | 0.00532 | 0.02488 | 0.04735 | 0.11736 |
| France | 0.05575 | 0.00148 | 0.00322 | 0.00599 | 0.00537 | 0.03002 | 0.05755 | 0.07646 |
| Germany | 0.01125 | 0.00016 | 0.00019 | 0.00026 | 0.00159 | 0.01508 | 0.03139 | 0.04542 |
| Italy | 0.08209 | 0.00436 | 0.00266 | 0.00369 | 0.00590 | 0.03431 | 0.05122 | 0.08229 |
| Japan | 0.01580 | 0.00049 | 0.00044 | 0.00102 | 0.00374 | 0.02343 | 0.04499 | 0.06483 |
| Netherlands | 0.09767 | 0.00362 | 0.00231 | 0.00384 | 0.00669 | 0.02712 | 0.04830 | 0.08296 |
| Norway | 0.03911 | 0.00299 | 0.00241 | 0.00325 | 0.00454 | 0.01686 | 0.02235 | 0.04836 |
| Spain | 0.06603 | 0.00259 | 0.00234 | 0.00358 | 0.00587 | 0.03573 | 0.03440 | 0.03142 |
| Sweden | 0.08862 | 0.00571 | 0.00261 | 0.00444 | 0.00945 | 0.03316 | 0.04673 | 0.09039 |
| Switzerland | 0.06970 | 0.00189 | 0.00184 | 0.00328 | 0.00793 | 0.03667 | 0.06074 | 0.10513 |
| United Kingdom | 0.06679 | 0.00319 | 0.00270 | 0.00403 | 0.00698 | 0.02246 | 0.03632 | 0.04949 |
| United States | 0.00679 | 0.00011 | 0.00013 | 0.00018 | 0.00211 | 0.00949 | 0.02035 | 0.01630 |
| SOURCE: Author's calculations. | ||||||||
Before turning to the ex-post validation results presented in the next section, it is important to discuss a number of findings in the literature that are relevant to this paper. Denton, Feavor, and Spencer (2005) use Canadian mortality data from 1926 to 2000 to produce long-term forecasts of life expectancy at birth and ages 65 and 80, based on the specification in equation (13) with p = 2 lags. The authors utilize a partially parametric method to generate random variation via a bootstrap procedure. They also implement a fully parametric approach by drawing from a multivariate normal disturbance process, much like the second model entertained in this paper. Although Denton, Feaver, and Spencer (2005) do not conduct an analysis of the out-of-sample forecast performance of these models, they do find the point forecasts generated by the fully parametric approach much closer to the projections of the Lee-Carter method than the official forecasts of the Canada Pension Plan.
Lee and Miller's (2001) ex-post validation analysis also focuses on life expectancy at birth e0, comparing actual and hypothetical forecast errors in the Lee-Carter model with those of the Social Security Administration (SSA).7 Using U.S. data from 1900 to 1998 (with 1921 as the initial jump-off year), the authors find that the empirical distribution of the actual forecast error matches well its hypothetical counterpart within a 10-year period, but deteriorates over time. Generally, the Lee-Carter model tends to underpredict life expectancy, although not by as much as the official SSA projections. In addition, the interval forecasts of e0 appear to be "too wide" up to the first 50 forecast horizons, while underestimating their hypothetical probability content for longer periods. Lee and Miller (2001) reach similar conclusions in more limited pseudo-forecast experiments using data from Japan, Canada, France, and Sweden.
Finally, Bell (1997) implements an evaluation of the short-term out-of-sample forecast behavior of multiple models using U.S. central death rates for white males and females from 1940 to 1991 (with 1981 as the initial jump-off year). Unlike Lee and Miller (2001), Bell reports forecast error over the entire age profile instead of relying on life expectancy as a single-valued measure of forecast performance. He finds that a univariate random-walk with drift fitted separately to each age group outperforms all of the parametric and nonparametric multivariate approaches considered. Only the Lee-Carter model with the type of bias correction discussed previously yields a similar forecast error to the univariate approach.
Out-of-Sample Forecast Performance
As previously mentioned, ex-post validation analysis provides a means to determine how well a set of models would have performed in the past, by comparing the forecasts generated by the models to the actual observations. This kind of analysis is not without its limitations, and should not be confused with forecasts that are generated in real time. The latter are produced prior to the forecast period, when the future outcome is truly uncertain. The former enjoy the advantage of perfect foresight, and are therefore based on an information set that was not available during the forecast period. Keeping these drawbacks in mind, ex-post validation is still a very valuable tool that cannot be replaced by in-sample goodness-of-fit measures. In particular, ex-post validation provides answers to "what if" type scenarios that are useful in specifying and calibrating models to be used for real time forecasting.
To compare forecast performance among several models, the following elements must be specified a priori: (1) the variables of interest to be projected; (2) the estimators used to measure these variables; and (3) an appropriate criterion to evaluate the variables' forecast performance. Clearly, with respect to the first point, the ultimate object of investigation is the 21 different age-specific mortality rates being modeled simultaneously. This paper looks at both the accuracy of the point projections produced by the models, and the ability of these projections to provide a realistic representation of forecast uncertainty. The means and medians of the generated forecast distributions are presented as two alternative point estimators. On the other hand, the capacity of the models to gauge forecast uncertainty is assessed by the behavior of their interval projections. To this aim, 90-percent confidence interval forecasts are also estimated using the 5th and 95th quantiles of the resulting forecast distributions.
The performance of the point estimates is evaluated using the traditional root mean squared error (RMSE) measure. Conversely, the performance of the interval projections is determined in terms of their empirical probability content (that is, the fraction of times the generated intervals actually include the observed ex-post mortality rates). If the interval forecasts enjoy an empirical probability content that is close to its hypothetical 90 percent level, it is likely that the model does a good job at accommodating the uncertainty associated with its point projections and can be used reliably for inference. However, coverage alone is only part of the picture. Since by design a fixed forecast interval between 0 and 1 covers the entire sample space, it is guaranteed to contain the ex-post mortality rates 100 percent of the time. Yet, such an interval has no practical use for inference, as it does not convey any information not already known a priori. Hence, the average width of the generated forecast intervals is also reported. Clearly, one unequivocal way to rank the interval estimates generated by several models involves the trade-off between probability coverage and interval width. In particular, an interval forecast that is narrower than all others and also enjoys greater empirical coverage should be the preferred choice.
Typically, when comparing multivariate forecast models, it is unusual for one model to outperform all others for every series projected at every forecast horizon. This is particularly likely in this application, given both the relatively large number of data sets and variables (21 age-specific mortality series for each of 16 samples). Therefore, to evaluate overall model performance, it is useful to adopt a single-valued measure that combines all the variables. One quantity to consider is life expectancy at birth , defined as the average number of remaining years an individual born at time t is expected to live. Following the discussion in Wilmoth (2004), let denote the number of survivors at age a in year t
out of an initial population arbitrarily set to , for a = 1,…,A. The person-years lived in the age interval [a, a + 1) is given by
with representing the average number of years lived within the age interval.8 Then, period life expectancy at birth is defined as follows
where denotes the person-years remaining at birth
Evidently, life expectancy at birth is a highly nonlinear function of all of the age-specific mortality rates that carries a natural interpretation. For this reason, it is often reported in practice as an overall summary measure of forecast performance, as in Lee and Miller's (2001) ex-post analysis. Unfortunately, such an aggregate quantity can be deceiving in that the forecast error associated with individual age groups could potentially cancel each other out in the computation of person-years remaining at birth, masking the extent of the forecast error experienced at particular ages.
Bell (1997) uses an alternative gauge of overall performance that looks at forecast error over the entire age profile. For instance, for the point projections, the RMSE corresponding to a particular forecast horizon is computed by averaging over the squared difference of observed and projected mortality at every age. This kind of measure is typical in multivariate time-series econometric applications. While not nearly as intuitive in its interpretation as life expectancy, it does not suffer from the potential problem that the forecast errors at different ages might cancel each other out. However, the measure is not without its drawbacks. In particular, suppose that a few of the series experience error that is disproportionately high relative to the remaining ages. Then, those few groups will largely determine the resulting total forecast error. A more robust measure of forecast error in the age profile might entail using a weighted average, with weights determined by the sample precision of each age series (that is, the inverse of its sample standard deviation). This more robust measure would define the importance of the error contributed by every age group as a function of how much variation mortality at that age displays in the sample, relative to the remaining series. Nevertheless, for the purposes of the forthcoming analysis, equal weights are assumed throughout.
In addition to both life expectancy at birth and the entire age profile as overall measures of forecast performance, the impact that mortality has on the program's future finances is an even more relevant criterion for a pay-as-you-go pension system. This impact is typically defined by the age distribution of the population, in terms of the old-age dependency ratio (the ratio of retired to working age population). Of course, to generate population forecasts, we would also need to model fertility and net migration, which is outside the scope of this paper. Nonetheless, it is still possible to evaluate the manner in which the age-specific mortality rates would actually enter into a population projection of the old-age dependency ratio, and thus, measure the effect that the mortality projections alone have on the program's finances. Specifically, recalling the previously defined number of survivors at age a in equation (21), the following dependency ratios implied by the individual age mortality rates are entertained:
At a given point in time t, refers to the ratio of survivors at ages 65 or older over those ages 20 to 64. Alternatively, embodies a more general measure of dependency encompassing both the youngest and oldest ages in the numerator (from birth to age 19, as well as ages 65 or older).
For the purpose of illustration, Charts 2 through 4 display a number of projections generated at the initial jump-off year using the mortality data for the United States and United Kingdom. The top graphs in Chart 2 show actual mortality for the 10–14 age group, along with the median and 90-percent interval forecasts generated by the models from 1980 to the end of each series. The bottom graphs display forecasts corresponding to the 70–74 age group. The top of Chart 3 presents similar projections of life expectancy at birth, while the bottom graphs illustrate different measures of the dependency ratios defined above. In particular, the thickest solid lines in the bottom part of Chart 3 respectively represent the historical values of and , based on the actual population figures from the Human Mortality Database. For instance, for the United States, the dependency ratios in the year 2000 were and .9 By contrast, the remaining lines in the same graphs represent the dependency ratios based on the mortality rates alone, abstracting from fertility and net migration. These are the quantities relevant to the ex-post analysis in this paper. Their values for the United States in 2000 were and . Chart 4 shows projections of these two dependency measures.
Mortality projections for ages 10–14 and ages 70–74 for the United States (1980–2002) and the United Kingdom (1980–2003)
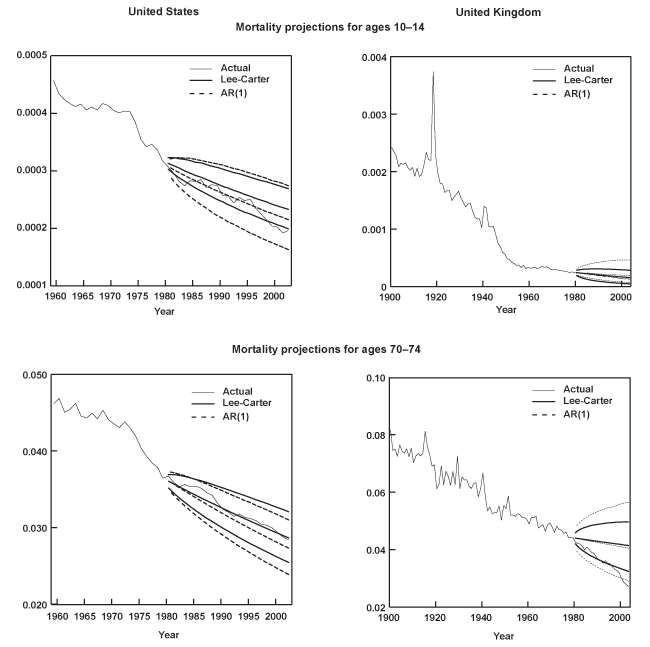
| Year | United States | United Kingdom | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Means | Lower bound | Upper bound | Actual | Means | Lower bound | Upper bound | |||||||
| Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | |||
| Mortality projections for ages 10–14 | ||||||||||||||
| 1900 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0024207 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1901 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0023447 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1902 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0022742 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1903 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0020826 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1904 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0021485 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1905 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0021253 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1906 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.002157 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1907 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0020725 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1908 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0020253 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1909 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.002075 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1910 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0019181 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1911 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0020605 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1912 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0019157 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1913 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.001952 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1914 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0021206 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1915 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0023367 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1916 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0022075 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1917 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.002197 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1918 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0037381 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1919 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0022892 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1920 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0019744 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1921 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0017965 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1922 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0017906 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1923 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0016385 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1924 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0016688 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1925 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0016727 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1926 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0014961 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1927 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0015593 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1928 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0016089 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1929 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0016602 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1930 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0015413 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1931 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0014696 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1932 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0013864 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1933 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0014354 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1934 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0014561 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1935 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.001317 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1936 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0012078 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1937 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0011765 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1938 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0011829 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1939 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0010251 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1940 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0013977 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1941 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0013689 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1942 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0010417 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1943 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0010383 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1944 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0010508 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1945 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0009142 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1946 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0007549 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1947 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0007006 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1948 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0005973 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1949 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0005637 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1950 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0004848 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1951 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0004714 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1952 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0004217 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1953 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0004005 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1954 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003694 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1955 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003776 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1956 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003318 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1957 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003736 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1958 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003148 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1959 | 0.0004572 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003342 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1960 | 0.0004345 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003216 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1961 | 0.0004243 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003263 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1962 | 0.0004166 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003368 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1963 | 0.0004119 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003151 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1964 | 0.0004158 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003267 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1965 | 0.0004058 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003517 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1966 | 0.0004112 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003354 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1967 | 0.0004055 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003451 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1968 | 0.0004166 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003278 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1969 | 0.0004138 | . . . | . . . | . . . | . . . | . . . | . . . | 0.000294 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1970 | 0.000405 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002966 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1971 | 0.0004007 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0003041 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1972 | 0.0004043 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002825 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1973 | 0.000403 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002777 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1974 | 0.0003838 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002762 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1975 | 0.0003546 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002598 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1976 | 0.0003421 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002596 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1977 | 0.0003459 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002431 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1978 | 0.0003369 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002559 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1979 | 0.0003171 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0002469 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1980 | 0.0003068 | 0.0003129 | 0.0003081 | 0.0003031 | 0.0002956 | 0.0003227 | 0.0003205 | 0.0002328 | 0.0002443 | 0.0002437 | 0.0001917 | 0.0002028 | 0.0003047 | 0.0002847 |
| 1981 | 0.0002962 | 0.0003088 | 0.0003021 | 0.0002953 | 0.0002825 | 0.0003226 | 0.000322 | 0.0002428 | 0.0002422 | 0.0002388 | 0.0001714 | 0.0001901 | 0.0003293 | 0.0002919 |
| 1982 | 0.000282 | 0.0003047 | 0.0002969 | 0.0002884 | 0.0002722 | 0.0003214 | 0.0003226 | 0.0002376 | 0.0002399 | 0.0002345 | 0.0001559 | 0.0001779 | 0.0003475 | 0.0002971 |
| 1983 | 0.0002741 | 0.0003005 | 0.000292 | 0.0002821 | 0.0002631 | 0.0003199 | 0.0003223 | 0.0002311 | 0.0002371 | 0.0002303 | 0.0001436 | 0.0001679 | 0.0003634 | 0.0003022 |
| 1984 | 0.000283 | 0.0002965 | 0.0002873 | 0.0002761 | 0.0002552 | 0.0003178 | 0.0003215 | 0.0002281 | 0.0002343 | 0.0002258 | 0.0001326 | 0.0001591 | 0.0003751 | 0.000304 |
| 1985 | 0.0002807 | 0.0002925 | 0.0002827 | 0.0002704 | 0.0002479 | 0.0003155 | 0.00032 | 0.0002406 | 0.0002322 | 0.0002216 | 0.0001233 | 0.000152 | 0.0003855 | 0.0003061 |
| 1986 | 0.0002848 | 0.0002886 | 0.0002782 | 0.0002649 | 0.0002411 | 0.0003135 | 0.0003184 | 0.0002029 | 0.0002297 | 0.0002173 | 0.0001148 | 0.0001439 | 0.0003981 | 0.000307 |
| 1987 | 0.0002711 | 0.0002848 | 0.0002738 | 0.0002597 | 0.0002346 | 0.0003111 | 0.0003163 | 0.0002119 | 0.0002276 | 0.0002136 | 0.0001074 | 0.0001376 | 0.0004075 | 0.0003071 |
| 1988 | 0.0002764 | 0.000281 | 0.0002694 | 0.0002552 | 0.0002281 | 0.0003083 | 0.0003141 | 0.0002083 | 0.0002254 | 0.0002093 | 0.0001022 | 0.0001312 | 0.000414 | 0.0003082 |
| 1989 | 0.000274 | 0.0002772 | 0.0002651 | 0.0002502 | 0.0002221 | 0.0003056 | 0.0003121 | 0.0001905 | 0.0002227 | 0.0002055 | 0.0000958 | 0.0001257 | 0.0004203 | 0.0003085 |
| 1990 | 0.0002573 | 0.0002735 | 0.0002609 | 0.0002456 | 0.0002166 | 0.0003029 | 0.0003097 | 0.0001901 | 0.0002205 | 0.0002017 | 0.0000904 | 0.0001204 | 0.0004263 | 0.0003084 |
| 1991 | 0.0002563 | 0.0002698 | 0.0002568 | 0.0002414 | 0.0002115 | 0.0003002 | 0.0003069 | 0.0001892 | 0.0002179 | 0.0001976 | 0.0000863 | 0.0001152 | 0.0004322 | 0.0003065 |
| 1992 | 0.0002443 | 0.0002661 | 0.0002527 | 0.0002369 | 0.0002066 | 0.0002973 | 0.0003044 | 0.0001676 | 0.0002153 | 0.000194 | 0.0000814 | 0.0001099 | 0.0004362 | 0.0003061 |
| 1993 | 0.0002538 | 0.0002626 | 0.0002486 | 0.0002325 | 0.0002018 | 0.0002946 | 0.0003017 | 0.0001856 | 0.0002132 | 0.0001905 | 0.0000768 | 0.0001055 | 0.0004417 | 0.0003051 |
| 1994 | 0.0002483 | 0.0002591 | 0.0002446 | 0.0002285 | 0.0001969 | 0.0002919 | 0.0002985 | 0.0001682 | 0.0002111 | 0.0001869 | 0.0000732 | 0.0001019 | 0.0004472 | 0.000303 |
| 1995 | 0.000251 | 0.0002557 | 0.0002408 | 0.0002245 | 0.0001922 | 0.0002891 | 0.0002959 | 0.000172 | 0.000209 | 0.0001834 | 0.0000696 | 0.0000969 | 0.0004513 | 0.0003018 |
| 1996 | 0.0002346 | 0.0002523 | 0.0002369 | 0.0002208 | 0.0001876 | 0.0002861 | 0.0002927 | 0.0001511 | 0.0002068 | 0.00018 | 0.0000668 | 0.0000936 | 0.0004527 | 0.0002993 |
| 1997 | 0.0002252 | 0.0002488 | 0.0002331 | 0.0002171 | 0.0001834 | 0.0002833 | 0.0002898 | 0.0001637 | 0.0002043 | 0.0001766 | 0.0000637 | 0.0000899 | 0.000457 | 0.0002983 |
| 1998 | 0.0002147 | 0.0002455 | 0.0002294 | 0.0002134 | 0.0001793 | 0.0002807 | 0.0002867 | 0.0001448 | 0.0002022 | 0.0001733 | 0.0000609 | 0.0000871 | 0.0004626 | 0.000296 |
| 1999 | 0.0002039 | 0.0002422 | 0.0002257 | 0.0002096 | 0.0001753 | 0.0002776 | 0.0002834 | 0.0001458 | 0.0001998 | 0.0001699 | 0.0000579 | 0.0000836 | 0.0004615 | 0.0002947 |
| 2000 | 0.000202 | 0.000239 | 0.0002221 | 0.0002061 | 0.0001713 | 0.0002747 | 0.0002805 | 0.0001363 | 0.0001977 | 0.0001667 | 0.0000553 | 0.0000804 | 0.0004628 | 0.0002912 |
| 2001 | 0.0001917 | 0.0002357 | 0.0002186 | 0.0002027 | 0.0001669 | 0.0002719 | 0.0002778 | 0.0001338 | 0.0001952 | 0.0001635 | 0.0000529 | 0.0000775 | 0.000465 | 0.0002903 |
| 2002 | 0.000196 | 0.0002326 | 0.000215 | 0.0001994 | 0.000163 | 0.0002688 | 0.0002745 | 0.000136 | 0.000193 | 0.0001602 | 0.0000508 | 0.000075 | 0.0004632 | 0.0002867 |
| 2003 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.000127 | 0.0001907 | 0.000157 | 0.0000483 | 0.0000725 | 0.0004652 | 0.0002836 |
| Mortality projections for ages 70–74 | ||||||||||||||
| 1900 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0816963 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1901 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0745112 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1902 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0750287 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1903 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0724764 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1904 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0764424 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1905 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0743151 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1906 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0735353 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1907 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0750804 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1908 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0723595 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1909 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0753843 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1910 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0702405 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1911 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0725824 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1912 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0734469 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1913 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0725917 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1914 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0734429 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1915 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0811731 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1916 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.075818 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1917 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0728859 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1918 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0690371 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1919 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0695904 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1920 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0611317 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1921 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.06271 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1922 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0691523 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1923 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0625077 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1924 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0673013 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1925 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.06552 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1926 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0623597 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1927 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0671793 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1928 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0625994 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1929 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0725803 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1930 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0612188 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1931 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0652902 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1932 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0642132 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1933 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0643448 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1934 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0621016 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1935 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0612652 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1936 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0629291 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1937 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0632869 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1938 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.058351 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1939 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0612099 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1940 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0666924 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1941 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0588152 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1942 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.053459 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1943 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0548969 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1944 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0525937 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1945 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0528416 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1946 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0529052 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1947 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0552472 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1948 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0502758 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1949 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.055392 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1950 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0542527 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1951 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0586028 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1952 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0519738 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1953 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0520523 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1954 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0515529 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1955 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0525442 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1956 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0522306 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1957 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0510936 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1958 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0511233 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1959 | 0.0461719 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0505895 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1960 | 0.0468548 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0489102 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1961 | 0.0450284 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0512965 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1962 | 0.045433 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0509973 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1963 | 0.0462092 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0517019 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1964 | 0.044542 | . . . | . . . | . . . | . . . | . . . | . . . | 0.047508 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1965 | 0.0442839 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0481592 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1966 | 0.0449404 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0486407 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1967 | 0.0441742 | . . . | . . . | . . . | . . . | . . . | . . . | 0.046405 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1968 | 0.0453161 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0486946 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1969 | 0.0440993 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0492901 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1970 | 0.043543 | . . . | . . . | . . . | . . . | . . . | . . . | 0.047866 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1971 | 0.0430527 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0460125 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1972 | 0.0437758 | . . . | . . . | . . . | . . . | . . . | . . . | 0.048175 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1973 | 0.0429815 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0469552 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1974 | 0.0419247 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0468322 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1975 | 0.0403599 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0456282 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1976 | 0.0393011 | . . . | . . . | . . . | . . . | . . . | . . . | 0.046132 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1977 | 0.0384311 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0441737 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1978 | 0.0378619 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0442123 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1979 | 0.0364247 | . . . | . . . | . . . | . . . | . . . | . . . | 0.0440767 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1980 | 0.0367298 | 0.0360475 | 0.0361306 | 0.0351788 | 0.034978 | 0.0369226 | 0.0372816 | 0.0426767 | 0.0439246 | 0.0439991 | 0.0420326 | 0.0398524 | 0.0458543 | 0.0481447 |
| 1981 | 0.0358571 | 0.0356793 | 0.035651 | 0.0344774 | 0.0341793 | 0.0369121 | 0.0371653 | 0.0420935 | 0.0437845 | 0.0438746 | 0.0411545 | 0.0391112 | 0.0465286 | 0.0487683 |
| 1982 | 0.0353292 | 0.0353142 | 0.0351988 | 0.0338532 | 0.0334699 | 0.0368093 | 0.0369568 | 0.0419784 | 0.0436431 | 0.0437718 | 0.0404303 | 0.0381301 | 0.0470007 | 0.0496449 |
| 1983 | 0.0356132 | 0.0349421 | 0.0347554 | 0.0332818 | 0.0328187 | 0.0366726 | 0.0367637 | 0.0412412 | 0.0434783 | 0.0436657 | 0.0398083 | 0.0375107 | 0.0473983 | 0.050268 |
| 1984 | 0.0353271 | 0.0345756 | 0.0343193 | 0.0327322 | 0.0322034 | 0.0364857 | 0.0365118 | 0.0398872 | 0.0433179 | 0.0435481 | 0.0392219 | 0.036803 | 0.0476799 | 0.0508353 |
| 1985 | 0.0353956 | 0.0342199 | 0.0338896 | 0.0322107 | 0.0316127 | 0.0362837 | 0.0362519 | 0.0409132 | 0.043174 | 0.0434269 | 0.0386853 | 0.0361545 | 0.047925 | 0.0513754 |
| 1986 | 0.0351402 | 0.0338627 | 0.0334647 | 0.0317051 | 0.0310656 | 0.0361017 | 0.0359659 | 0.0400283 | 0.043019 | 0.0433219 | 0.0381726 | 0.0356729 | 0.0482165 | 0.0518323 |
| 1987 | 0.0345645 | 0.0335158 | 0.0330385 | 0.0312201 | 0.0305019 | 0.0358866 | 0.0356929 | 0.0389972 | 0.0428795 | 0.0432019 | 0.037694 | 0.0350882 | 0.0484275 | 0.0522774 |
| 1988 | 0.0342236 | 0.0331711 | 0.0326166 | 0.0308004 | 0.0299674 | 0.0356455 | 0.0353556 | 0.0387626 | 0.042737 | 0.0430808 | 0.0373477 | 0.0346118 | 0.0485724 | 0.0526241 |
| 1989 | 0.0331623 | 0.0328221 | 0.0322024 | 0.0303378 | 0.0294489 | 0.035403 | 0.035076 | 0.0375397 | 0.0425768 | 0.042997 | 0.0368983 | 0.0341742 | 0.0487103 | 0.0530628 |
| 1990 | 0.032391 | 0.0324814 | 0.0318069 | 0.0299001 | 0.02898 | 0.0351592 | 0.034769 | 0.0363912 | 0.0424282 | 0.0428569 | 0.0364934 | 0.03372 | 0.0488411 | 0.0532738 |
| 1991 | 0.0319857 | 0.0321424 | 0.0313979 | 0.0295076 | 0.0284773 | 0.0349151 | 0.0344407 | 0.0361483 | 0.042275 | 0.0427155 | 0.036179 | 0.0332384 | 0.0489674 | 0.0537261 |
| 1992 | 0.0314667 | 0.0318021 | 0.0310012 | 0.029081 | 0.0280097 | 0.0346563 | 0.0341166 | 0.0352667 | 0.042112 | 0.0426431 | 0.0357804 | 0.0329287 | 0.0490521 | 0.0539293 |
| 1993 | 0.0317406 | 0.0314728 | 0.0306134 | 0.0286658 | 0.0275291 | 0.0344109 | 0.0338498 | 0.0361278 | 0.0419672 | 0.0425066 | 0.0353977 | 0.0323742 | 0.0491668 | 0.0543318 |
| 1994 | 0.0313307 | 0.0311501 | 0.0302331 | 0.0282827 | 0.0271315 | 0.0341674 | 0.0335148 | 0.0352611 | 0.04183 | 0.0424206 | 0.0350774 | 0.0320004 | 0.049282 | 0.0545508 |
| 1995 | 0.031179 | 0.0308289 | 0.0298581 | 0.027897 | 0.0266721 | 0.0339134 | 0.0332583 | 0.03511 | 0.0416889 | 0.0423114 | 0.0347429 | 0.0315927 | 0.0493653 | 0.0547197 |
| 1996 | 0.030918 | 0.03051 | 0.0294798 | 0.0275475 | 0.0262684 | 0.0336405 | 0.0329104 | 0.034058 | 0.0415459 | 0.0421898 | 0.0344811 | 0.0313569 | 0.0493939 | 0.0548686 |
| 1997 | 0.0304351 | 0.0301894 | 0.029107 | 0.0271831 | 0.0258186 | 0.0333927 | 0.0326233 | 0.0331901 | 0.0413909 | 0.042064 | 0.0341775 | 0.0309142 | 0.0494836 | 0.0551301 |
| 1998 | 0.0303015 | 0.0298772 | 0.0287438 | 0.0268274 | 0.0254172 | 0.0331548 | 0.0322937 | 0.0327514 | 0.0412489 | 0.0419755 | 0.0338857 | 0.0306393 | 0.0495953 | 0.0554585 |
| 1999 | 0.0299566 | 0.0295652 | 0.0283827 | 0.0264634 | 0.0250394 | 0.0328692 | 0.0319924 | 0.0318893 | 0.0410996 | 0.0418846 | 0.0335666 | 0.0303119 | 0.0495731 | 0.0557305 |
| 2000 | 0.0293229 | 0.0292584 | 0.0280223 | 0.0261179 | 0.0246348 | 0.0326041 | 0.0316658 | 0.0299647 | 0.0409561 | 0.0417675 | 0.0332816 | 0.0300506 | 0.0496001 | 0.0559626 |
| 2001 | 0.0287526 | 0.0289503 | 0.0276726 | 0.0257801 | 0.0242588 | 0.0323475 | 0.0313411 | 0.028635 | 0.0408016 | 0.0416216 | 0.0330064 | 0.0296909 | 0.0496448 | 0.0561353 |
| 2002 | 0.0284218 | 0.0286494 | 0.0273251 | 0.025456 | 0.023881 | 0.0320639 | 0.0309917 | 0.0279082 | 0.0406581 | 0.0415482 | 0.0327551 | 0.0294402 | 0.049609 | 0.0563574 |
| 2003 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.0271602 | 0.0405017 | 0.041398 | 0.032443 | 0.0290366 | 0.0496477 | 0.0563662 |
Life expectancy at birth and old-age dependency ratios for the United States and the United Kingdom
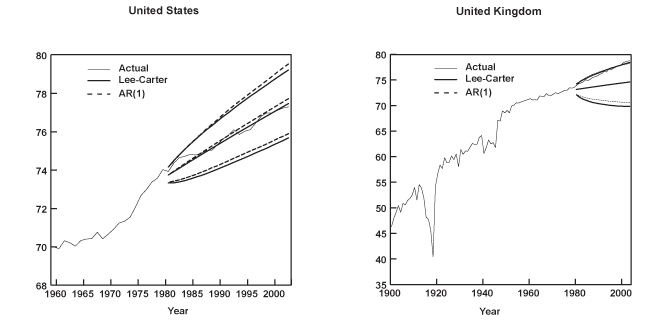
| Year | United States | United Kingdom | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Means | Lower bound | Upper bound | Actual | Means | Lower bound | Upper bound | |||||||
| Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | |||
| 1900 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 46.32 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1901 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 47.91 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1902 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 49.08 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1903 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 50.43 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1904 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 49.11 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1905 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 50.86 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1906 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 50.58 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1907 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 51.44 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1908 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 51.84 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1909 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 52.52 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1910 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 53.99 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1911 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 51.54 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1912 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 54.55 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1913 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 53.83 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1914 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 51.99 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1915 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 48.2 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1916 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 47.73 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1917 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 45.57 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1918 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 40.43 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1919 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 54.12 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1920 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 56.6 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1921 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 58.35 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1922 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 57.69 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1923 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 59.79 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1924 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 58.79 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1925 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 58.94 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1926 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 60.13 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1927 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 59.42 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1928 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 60.52 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1929 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 58.03 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1930 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.41 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1931 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 60.46 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1932 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.13 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1933 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.06 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1934 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.84 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1935 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62.6 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1936 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62.37 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1937 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62.42 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1938 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 63.78 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1939 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 64.13 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1940 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 60.62 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1941 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.77 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1942 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 63.27 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1943 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62.51 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1944 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 62.74 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1945 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 61.77 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1946 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 67.11 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1947 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 66.94 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1948 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 68.94 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1949 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 68.56 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1950 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 69.03 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1951 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 68.58 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1952 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 69.91 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1953 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 70.11 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1954 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 70.53 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1955 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 70.48 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1956 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 70.7 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1957 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 70.85 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1958 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 71.02 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1959 | 70 | . . . | . . . | . . . | . . . | . . . | . . . | 71.14 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1960 | 69.91 | . . . | . . . | . . . | . . . | . . . | . . . | 71.35 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1961 | 70.32 | . . . | . . . | . . . | . . . | . . . | . . . | 71.08 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1962 | 70.21 | . . . | . . . | . . . | . . . | . . . | . . . | 71.13 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1963 | 70.04 | . . . | . . . | . . . | . . . | . . . | . . . | 71.06 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1964 | 70.33 | . . . | . . . | . . . | . . . | . . . | . . . | 71.84 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1965 | 70.41 | . . . | . . . | . . . | . . . | . . . | . . . | 71.83 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1966 | 70.43 | . . . | . . . | . . . | . . . | . . . | . . . | 71.75 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1967 | 70.76 | . . . | . . . | . . . | . . . | . . . | . . . | 72.33 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1968 | 70.42 | . . . | . . . | . . . | . . . | . . . | . . . | 71.98 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1969 | 70.66 | . . . | . . . | . . . | . . . | . . . | . . . | 71.95 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1970 | 70.92 | . . . | . . . | . . . | . . . | . . . | . . . | 72.21 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1971 | 71.24 | . . . | . . . | . . . | . . . | . . . | . . . | 72.51 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1972 | 71.34 | . . . | . . . | . . . | . . . | . . . | . . . | 72.31 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1973 | 71.54 | . . . | . . . | . . . | . . . | . . . | . . . | 72.54 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1974 | 72.08 | . . . | . . . | . . . | . . . | . . . | . . . | 72.74 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1975 | 72.68 | . . . | . . . | . . . | . . . | . . . | . . . | 72.98 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1976 | 72.99 | . . . | . . . | . . . | . . . | . . . | . . . | 72.98 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1977 | 73.38 | . . . | . . . | . . . | . . . | . . . | . . . | 73.47 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1978 | 73.58 | . . . | . . . | . . . | . . . | . . . | . . . | 73.4 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1979 | 74.03 | . . . | . . . | . . . | . . . | . . . | . . . | 73.51 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1980 | 73.93 | 73.7458606 | 73.7424645 | 73.3322964 | 73.3744012 | 74.1588641 | 74.1207725 | 73.93 | 73.1353627 | 73.1448765 | 72.1051362 | 72.1367773 | 74.1046041 | 74.2127779 |
| 1981 | 74.36 | 73.9214999 | 73.9482411 | 73.3372461 | 73.4238732 | 74.4962195 | 74.4761286 | 74.27 | 73.1962983 | 73.2174636 | 71.7233955 | 71.974905 | 74.5292525 | 74.4868189 |
| 1982 | 74.65 | 74.0964728 | 74.1412297 | 73.3855638 | 73.4926295 | 74.7991497 | 74.7914782 | 74.41 | 73.2582854 | 73.2849311 | 71.4504257 | 71.8042389 | 74.8709557 | 74.8188381 |
| 1983 | 74.72 | 74.2756519 | 74.3345326 | 73.4498358 | 73.5790698 | 75.0787815 | 75.0803481 | 74.64 | 73.3319261 | 73.3475689 | 71.2167245 | 71.6371386 | 75.1586427 | 75.050837 |
| 1984 | 74.82 | 74.4529684 | 74.5231223 | 73.5379033 | 73.6745313 | 75.3500606 | 75.3658531 | 75.04 | 73.4035214 | 73.414565 | 71.0490944 | 71.531685 | 75.4252055 | 75.2730263 |
| 1985 | 74.79 | 74.6260022 | 74.7099316 | 73.6332772 | 73.7716289 | 75.6096447 | 75.6257676 | 74.87 | 73.4659906 | 73.4802635 | 70.9016857 | 71.4297037 | 75.6653614 | 75.509256 |
| 1986 | 74.88 | 74.8006506 | 74.8936972 | 73.7194318 | 73.8883308 | 75.8634546 | 75.8847774 | 75.15 | 73.5339324 | 73.5472374 | 70.7245616 | 71.3306281 | 75.8916431 | 75.7097458 |
| 1987 | 75.02 | 74.9711474 | 75.080426 | 73.8213974 | 73.9954708 | 76.1090523 | 76.1509465 | 75.49 | 73.5941908 | 73.6098276 | 70.5950554 | 71.2340237 | 76.1001508 | 75.9307937 |
| 1988 | 75.04 | 75.1413792 | 75.2646897 | 73.9360401 | 74.1291725 | 76.323306 | 76.3938246 | 75.61 | 73.6562228 | 73.6777696 | 70.5055569 | 71.2079548 | 76.249494 | 76.108558 |
| 1989 | 75.33 | 75.3146478 | 75.4488433 | 74.0516681 | 74.2282228 | 76.5614048 | 76.632507 | 75.77 | 73.7273567 | 73.7355675 | 70.4199067 | 71.1321584 | 76.4413949 | 76.2676077 |
| 1990 | 75.62 | 75.4848105 | 75.626962 | 74.1682659 | 74.3615088 | 76.7887194 | 76.8991415 | 76.09 | 73.7920407 | 73.8039585 | 70.3381861 | 71.0792051 | 76.6125357 | 76.4426103 |
| 1991 | 75.83 | 75.6550589 | 75.809569 | 74.2853486 | 74.4845579 | 76.994211 | 77.1349353 | 76.25 | 73.8599667 | 73.8753563 | 70.2589202 | 71.0311574 | 76.7443852 | 76.6312971 |
| 1992 | 76.11 | 75.8269665 | 75.9911667 | 74.4099229 | 74.6207454 | 77.2194189 | 77.370641 | 76.67 | 73.9315759 | 73.9308582 | 70.2055627 | 70.9463259 | 76.9101668 | 76.8024397 |
| 1993 | 75.86 | 75.9943969 | 76.1702346 | 74.5283676 | 74.7443354 | 77.4406055 | 77.5896512 | 76.56 | 73.9937902 | 73.9991874 | 70.1329906 | 70.9205528 | 77.0680069 | 76.9847729 |
| 1994 | 76.03 | 76.1592998 | 76.3469464 | 74.6463273 | 74.870888 | 77.6464759 | 77.8047289 | 77.1 | 74.0532974 | 74.0555367 | 70.0597993 | 70.8439722 | 77.1991197 | 77.118572 |
| 1995 | 76.11 | 76.3245189 | 76.5202437 | 74.7698077 | 75.0011522 | 77.8555064 | 78.0254908 | 76.99 | 74.1144059 | 74.1205818 | 70.0066054 | 70.8376 | 77.3351719 | 77.3311714 |
| 1996 | 76.46 | 76.4894902 | 76.6955717 | 74.90297 | 75.1178989 | 78.0465402 | 78.2454404 | 77.27 | 74.1763761 | 74.1787314 | 69.9883123 | 70.7904276 | 77.4410159 | 77.429593 |
| 1997 | 76.81 | 76.6562814 | 76.8705997 | 75.0243406 | 75.238009 | 78.2474305 | 78.4492198 | 77.51 | 74.2448536 | 74.2427378 | 69.9308317 | 70.7602873 | 77.5630892 | 77.5878031 |
| 1998 | 76.98 | 76.8197745 | 77.0431179 | 75.1412612 | 75.3644395 | 78.4451846 | 78.670305 | 77.66 | 74.3061821 | 74.3016275 | 69.858952 | 70.6916607 | 77.6798211 | 77.7350728 |
| 1999 | 76.97 | 76.984124 | 77.2152925 | 75.2821993 | 75.5037002 | 78.6493881 | 78.8907751 | 77.78 | 74.3719972 | 74.3548218 | 69.8732452 | 70.6731174 | 77.8067357 | 77.8569343 |
| 2000 | 77.12 | 77.1468763 | 77.3879826 | 75.4136216 | 75.6457343 | 78.8449413 | 79.1199582 | 78.26 | 74.4338208 | 74.4186347 | 69.8558424 | 70.6382197 | 77.9194859 | 78.0128717 |
| 2001 | 77.24 | 77.3113083 | 77.5576754 | 75.5413425 | 75.7676327 | 79.0378196 | 79.3336859 | 78.53 | 74.5017189 | 74.4850654 | 69.826991 | 70.6408922 | 78.0278583 | 78.1402039 |
| 2002 | 77.3 | 77.4730359 | 77.7283145 | 75.6830945 | 75.9034326 | 79.2244957 | 79.537497 | 78.67 | 74.5638709 | 74.5379541 | 69.8501511 | 70.6128084 | 78.1264205 | 78.2843643 |
| 2003 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 78.73 | 74.6317542 | 74.6038034 | 69.8251071 | 70.5976839 | 78.2482756 | 78.4084493 |
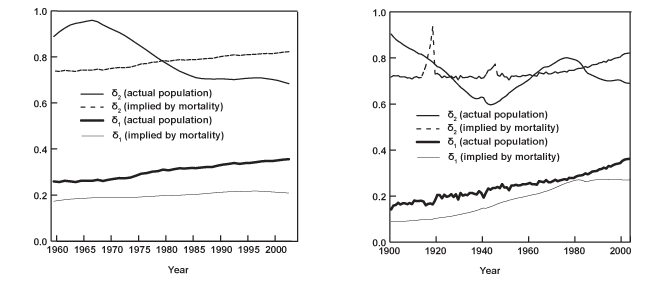
| Year | United States | United Kingdom | ||||||
|---|---|---|---|---|---|---|---|---|
| δ1 (Actual Population) |
δ1 (Implied by Mortality) |
δ2 (Actual Population) |
δ2 (Implied by Mortality) |
δ1 (Actual Population) |
δ1 (Implied by Mortality) |
δ2 (Actual Population) |
δ2 (Implied by Mortality) |
|
| 1900 | . . . | . . . | . . . | . . . | 0.0893 | 0.142 | 0.904 | 0.7171 |
| 1901 | . . . | . . . | . . . | . . . | 0.0884 | 0.159 | 0.8916 | 0.7234 |
| 1902 | . . . | . . . | . . . | . . . | 0.0885 | 0.1611 | 0.8811 | 0.7221 |
| 1903 | . . . | . . . | . . . | . . . | 0.089 | 0.1708 | 0.873 | 0.7231 |
| 1904 | . . . | . . . | . . . | . . . | 0.0898 | 0.1635 | 0.8672 | 0.7178 |
| 1905 | . . . | . . . | . . . | . . . | 0.0899 | 0.1687 | 0.8593 | 0.7183 |
| 1906 | . . . | . . . | . . . | . . . | 0.0908 | 0.1684 | 0.8529 | 0.7178 |
| 1907 | . . . | . . . | . . . | . . . | 0.0918 | 0.165 | 0.8467 | 0.7129 |
| 1908 | . . . | . . . | . . . | . . . | 0.0925 | 0.1697 | 0.8409 | 0.7138 |
| 1909 | . . . | . . . | . . . | . . . | 0.093 | 0.1653 | 0.8364 | 0.7086 |
| 1910 | . . . | . . . | . . . | . . . | 0.0934 | 0.1807 | 0.8312 | 0.7162 |
| 1911 | . . . | . . . | . . . | . . . | 0.0947 | 0.1782 | 0.8246 | 0.719 |
| 1912 | . . . | . . . | . . . | . . . | 0.0961 | 0.1789 | 0.818 | 0.7139 |
| 1913 | . . . | . . . | . . . | . . . | 0.0973 | 0.1798 | 0.8167 | 0.7152 |
| 1914 | . . . | . . . | . . . | . . . | 0.0977 | 0.1764 | 0.8107 | 0.738 |
| 1915 | . . . | . . . | . . . | . . . | 0.0978 | 0.1599 | 0.8036 | 0.7656 |
| 1916 | . . . | . . . | . . . | . . . | 0.0979 | 0.1663 | 0.7961 | 0.8138 |
| 1917 | . . . | . . . | . . . | . . . | 0.0986 | 0.168 | 0.7895 | 0.857 |
| 1918 | . . . | . . . | . . . | . . . | 0.0999 | 0.1639 | 0.7814 | 0.9359 |
| 1919 | . . . | . . . | . . . | . . . | 0.1025 | 0.1814 | 0.7716 | 0.7304 |
| 1920 | . . . | . . . | . . . | . . . | 0.1043 | 0.2052 | 0.7621 | 0.7327 |
| 1921 | . . . | . . . | . . . | . . . | 0.1058 | 0.2046 | 0.7592 | 0.7258 |
| 1922 | . . . | . . . | . . . | . . . | 0.1073 | 0.1903 | 0.7522 | 0.7142 |
| 1923 | . . . | . . . | . . . | . . . | 0.1081 | 0.206 | 0.7436 | 0.7219 |
| 1924 | . . . | . . . | . . . | . . . | 0.1096 | 0.197 | 0.7351 | 0.7149 |
| 1925 | . . . | . . . | . . . | . . . | 0.1104 | 0.2 | 0.7245 | 0.7168 |
| 1926 | . . . | . . . | . . . | . . . | 0.1121 | 0.208 | 0.7146 | 0.721 |
| 1927 | . . . | . . . | . . . | . . . | 0.1145 | 0.1963 | 0.7053 | 0.7126 |
| 1928 | . . . | . . . | . . . | . . . | 0.1163 | 0.208 | 0.694 | 0.7207 |
| 1929 | . . . | . . . | . . . | . . . | 0.1187 | 0.1848 | 0.6841 | 0.7047 |
| 1930 | . . . | . . . | . . . | . . . | 0.12 | 0.2134 | 0.673 | 0.7238 |
| 1931 | . . . | . . . | . . . | . . . | 0.1231 | 0.202 | 0.6656 | 0.7141 |
| 1932 | . . . | . . . | . . . | . . . | 0.1252 | 0.2061 | 0.657 | 0.7152 |
| 1933 | . . . | . . . | . . . | . . . | 0.127 | 0.204 | 0.6487 | 0.7156 |
| 1934 | . . . | . . . | . . . | . . . | 0.1291 | 0.2136 | 0.6387 | 0.7207 |
| 1935 | . . . | . . . | . . . | . . . | 0.132 | 0.2139 | 0.6306 | 0.7181 |
| 1936 | . . . | . . . | . . . | . . . | 0.1348 | 0.2097 | 0.625 | 0.713 |
| 1937 | . . . | . . . | . . . | . . . | 0.1377 | 0.207 | 0.6229 | 0.7107 |
| 1938 | . . . | . . . | . . . | . . . | 0.141 | 0.2213 | 0.6246 | 0.7205 |
| 1939 | . . . | . . . | . . . | . . . | 0.1455 | 0.2134 | 0.6305 | 0.7113 |
| 1940 | . . . | . . . | . . . | . . . | 0.148 | 0.1933 | 0.6273 | 0.714 |
| 1941 | . . . | . . . | . . . | . . . | 0.1472 | 0.2148 | 0.6077 | 0.7276 |
| 1942 | . . . | . . . | . . . | . . . | 0.1501 | 0.2329 | 0.5994 | 0.7462 |
| 1943 | . . . | . . . | . . . | . . . | 0.1539 | 0.2277 | 0.5965 | 0.749 |
| 1944 | . . . | . . . | . . . | . . . | 0.1576 | 0.2352 | 0.5984 | 0.7601 |
| 1945 | . . . | . . . | . . . | . . . | 0.1616 | 0.2347 | 0.6024 | 0.7735 |
| 1946 | . . . | . . . | . . . | . . . | 0.1661 | 0.2398 | 0.6084 | 0.726 |
| 1947 | . . . | . . . | . . . | . . . | 0.1696 | 0.2344 | 0.6139 | 0.7204 |
| 1948 | . . . | . . . | . . . | . . . | 0.1729 | 0.2519 | 0.6241 | 0.7338 |
| 1949 | . . . | . . . | . . . | . . . | 0.1764 | 0.2369 | 0.6301 | 0.7183 |
| 1950 | . . . | . . . | . . . | . . . | 0.1784 | 0.2381 | 0.6374 | 0.7173 |
| 1951 | . . . | . . . | . . . | . . . | 0.1822 | 0.2255 | 0.6481 | 0.7041 |
| 1952 | . . . | . . . | . . . | . . . | 0.1841 | 0.2455 | 0.6555 | 0.721 |
| 1953 | . . . | . . . | . . . | . . . | 0.1871 | 0.2461 | 0.6632 | 0.7205 |
| 1954 | . . . | . . . | . . . | . . . | 0.1899 | 0.2491 | 0.671 | 0.7226 |
| 1955 | . . . | . . . | . . . | . . . | 0.1921 | 0.2459 | 0.6771 | 0.7189 |
| 1956 | . . . | . . . | . . . | . . . | 0.1939 | 0.2473 | 0.6821 | 0.7193 |
| 1957 | . . . | . . . | . . . | . . . | 0.1959 | 0.2519 | 0.688 | 0.7245 |
| 1958 | . . . | . . . | . . . | . . . | 0.1986 | 0.251 | 0.6949 | 0.7226 |
| 1959 | 0.1731 | 0.2589 | 0.8885 | 0.7392 | 0.2006 | 0.2535 | 0.7016 | 0.725 |
| 1960 | 0.1765 | 0.2565 | 0.9089 | 0.737 | 0.2028 | 0.2572 | 0.7091 | 0.7283 |
| 1961 | 0.1796 | 0.2619 | 0.9251 | 0.7414 | 0.2054 | 0.2512 | 0.7194 | 0.7226 |
| 1962 | 0.1821 | 0.2593 | 0.9385 | 0.7392 | 0.2074 | 0.2518 | 0.7285 | 0.7231 |
| 1963 | 0.1837 | 0.2564 | 0.9457 | 0.7369 | 0.209 | 0.2494 | 0.736 | 0.7209 |
| 1964 | 0.1848 | 0.2622 | 0.9498 | 0.7428 | 0.2113 | 0.2649 | 0.7436 | 0.736 |
| 1965 | 0.1864 | 0.2621 | 0.955 | 0.7426 | 0.2153 | 0.2625 | 0.7522 | 0.7335 |
| 1966 | 0.1878 | 0.2615 | 0.9592 | 0.7425 | 0.2183 | 0.2601 | 0.7595 | 0.731 |
| 1967 | 0.1883 | 0.2661 | 0.9529 | 0.7468 | 0.2207 | 0.2695 | 0.7611 | 0.7393 |
| 1968 | 0.188 | 0.2611 | 0.9389 | 0.7429 | 0.2242 | 0.2606 | 0.7624 | 0.7304 |
| 1969 | 0.188 | 0.2663 | 0.9273 | 0.7481 | 0.2279 | 0.2603 | 0.7675 | 0.7307 |
| 1970 | 0.1881 | 0.2702 | 0.9163 | 0.7515 | 0.2322 | 0.265 | 0.7739 | 0.7348 |
| 1971 | 0.1883 | 0.2735 | 0.9057 | 0.7541 | 0.2365 | 0.271 | 0.78 | 0.7404 |
| 1972 | 0.1886 | 0.2727 | 0.8925 | 0.753 | 0.2411 | 0.2647 | 0.7868 | 0.7343 |
| 1973 | 0.1893 | 0.2758 | 0.877 | 0.7557 | 0.2452 | 0.2683 | 0.7926 | 0.7377 |
| 1974 | 0.1902 | 0.2837 | 0.8608 | 0.7619 | 0.2496 | 0.2708 | 0.7968 | 0.7397 |
| 1975 | 0.1916 | 0.2927 | 0.845 | 0.7696 | 0.2539 | 0.2737 | 0.8 | 0.7421 |
| 1976 | 0.1933 | 0.2953 | 0.8291 | 0.7711 | 0.2577 | 0.2707 | 0.8012 | 0.7389 |
| 1977 | 0.1945 | 0.3015 | 0.8119 | 0.7768 | 0.2605 | 0.2793 | 0.799 | 0.7467 |
| 1978 | 0.1959 | 0.3035 | 0.7953 | 0.7783 | 0.2638 | 0.2784 | 0.7963 | 0.7463 |
| 1979 | 0.1973 | 0.3104 | 0.7801 | 0.7845 | 0.2669 | 0.2787 | 0.7937 | 0.7461 |
| 1980 | 0.198 | 0.3071 | 0.7658 | 0.7811 | 0.2693 | 0.2849 | 0.7906 | 0.7514 |
| 1981 | 0.1987 | 0.3123 | 0.7515 | 0.7853 | 0.2706 | 0.2887 | 0.7849 | 0.7546 |
| 1982 | 0.1992 | 0.3161 | 0.7382 | 0.7879 | 0.27 | 0.2895 | 0.7756 | 0.7549 |
| 1983 | 0.2006 | 0.3152 | 0.7281 | 0.7863 | 0.267 | 0.2921 | 0.7619 | 0.757 |
| 1984 | 0.2017 | 0.3172 | 0.7184 | 0.7882 | 0.2628 | 0.2987 | 0.7446 | 0.7631 |
| 1985 | 0.2028 | 0.3168 | 0.7099 | 0.7878 | 0.263 | 0.2944 | 0.7337 | 0.7585 |
| 1986 | 0.2046 | 0.3195 | 0.7061 | 0.791 | 0.2663 | 0.2999 | 0.7292 | 0.7637 |
| 1987 | 0.2069 | 0.3218 | 0.7044 | 0.793 | 0.2687 | 0.3067 | 0.7245 | 0.7702 |
| 1988 | 0.2089 | 0.3219 | 0.704 | 0.7934 | 0.2702 | 0.308 | 0.7199 | 0.7713 |
| 1989 | 0.2108 | 0.3278 | 0.7041 | 0.799 | 0.2711 | 0.3095 | 0.7152 | 0.7724 |
| 1990 | 0.2127 | 0.3323 | 0.7045 | 0.8032 | 0.2712 | 0.316 | 0.7106 | 0.7788 |
| 1991 | 0.214 | 0.3351 | 0.7029 | 0.8059 | 0.2715 | 0.3177 | 0.7072 | 0.7801 |
| 1992 | 0.2145 | 0.339 | 0.7015 | 0.8093 | 0.2716 | 0.3236 | 0.7039 | 0.7854 |
| 1993 | 0.2158 | 0.3353 | 0.7038 | 0.8061 | 0.2717 | 0.3197 | 0.7014 | 0.7815 |
| 1994 | 0.2166 | 0.3386 | 0.7065 | 0.8093 | 0.2715 | 0.3304 | 0.7002 | 0.7917 |
| 1995 | 0.2169 | 0.3397 | 0.708 | 0.8102 | 0.2719 | 0.3284 | 0.7007 | 0.7899 |
| 1996 | 0.2172 | 0.3427 | 0.7091 | 0.8116 | 0.2721 | 0.3344 | 0.7016 | 0.7956 |
| 1997 | 0.2166 | 0.3463 | 0.7086 | 0.8138 | 0.2724 | 0.3387 | 0.7034 | 0.7995 |
| 1998 | 0.2151 | 0.3483 | 0.7053 | 0.815 | 0.2724 | 0.3408 | 0.7049 | 0.8014 |
| 1999 | 0.2133 | 0.3478 | 0.702 | 0.8143 | 0.2716 | 0.3432 | 0.7035 | 0.8036 |
| 2000 | 0.2117 | 0.3507 | 0.6976 | 0.8173 | 0.2701 | 0.353 | 0.6984 | 0.8131 |
| 2001 | 0.2101 | 0.3538 | 0.6906 | 0.8206 | 0.2696 | 0.3586 | 0.6934 | 0.8184 |
| 2002 | 0.2086 | 0.3558 | 0.6837 | 0.8226 | 0.2699 | 0.3607 | 0.6909 | 0.8202 |
| 2003 | . . . | . . . | . . . | . . . | 0.2705 | 0.3618 | 0.6899 | 0.8212 |
Projections of old-age dependency ratios for the United States (1980–2002) and the United Kingdom
(1980–2003)
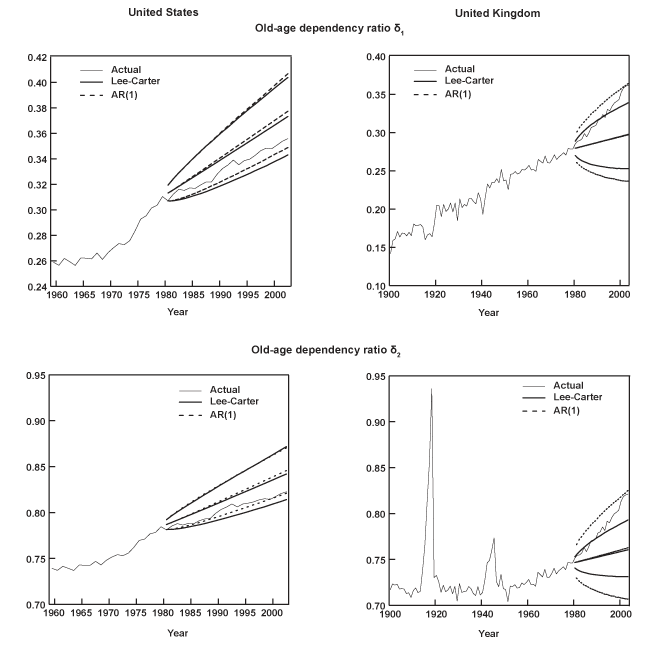
| Year | United States | United Kingdom | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Means | Lower bound | Upper bound | Actual | Means | Lower bound | Upper bound | |||||||
| Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | Lee-Carter | AR(1) | |||
| Old-age dependency ratio δ1 | ||||||||||||||
| 1900 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.142 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1901 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.159 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1902 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1611 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1903 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1708 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1904 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1635 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1905 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1687 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1906 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1684 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1907 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.165 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1908 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1697 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1909 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1653 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1910 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1807 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1911 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1782 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1912 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1789 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1913 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1798 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1914 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1764 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1915 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1599 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1916 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1663 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1917 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.168 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1918 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1639 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1919 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1814 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1920 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2052 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1921 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2046 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1922 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1903 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1923 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.206 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1924 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.197 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1925 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1926 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.208 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1927 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1963 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1928 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.208 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1929 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1848 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1930 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2134 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1931 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.202 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1932 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2061 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1933 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.204 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1934 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2136 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1935 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2139 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1936 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2097 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1937 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.207 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1938 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2213 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1939 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2134 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1940 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.1933 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1941 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2148 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1942 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2329 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1943 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2277 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1944 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2352 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1945 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2347 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1946 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2398 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1947 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2344 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1948 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2519 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1949 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2369 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1950 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2381 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1951 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2255 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1952 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2455 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1953 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2461 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1954 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2491 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1955 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2459 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1956 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2473 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1957 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.2519 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1958 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.251 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1959 | 0.2589 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2535 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1960 | 0.2565 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2572 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1961 | 0.2619 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2512 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1962 | 0.2593 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2518 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1963 | 0.2564 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2494 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1964 | 0.2622 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2649 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1965 | 0.2621 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2625 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1966 | 0.2615 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2601 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1967 | 0.2661 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2695 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1968 | 0.2611 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2606 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1969 | 0.2663 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2603 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1970 | 0.2702 | . . . | . . . | . . . | . . . | . . . | . . . | 0.265 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1971 | 0.2735 | . . . | . . . | . . . | . . . | . . . | . . . | 0.271 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1972 | 0.2727 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2647 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1973 | 0.2758 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2683 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1974 | 0.2837 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2708 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1975 | 0.2927 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2737 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1976 | 0.2953 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2707 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1977 | 0.3015 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2793 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1978 | 0.3035 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2784 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1979 | 0.3104 | . . . | . . . | . . . | . . . | . . . | . . . | 0.2787 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1980 | 0.3071 | 0.3131 | 0.3127 | 0.3070244 | 0.3064707 | 0.3192484 | 0.3191011 | 0.2849 | 0.2794 | 0.2796 | 0.2702205 | 0.2624991 | 0.2885771 | 0.2980753 |
| 1981 | 0.3123 | 0.3157 | 0.3158 | 0.3070961 | 0.3073612 | 0.3243779 | 0.3243557 | 0.2887 | 0.2801 | 0.2803 | 0.2670679 | 0.2599317 | 0.2929205 | 0.3018957 |
| 1982 | 0.3161 | 0.3184 | 0.3186 | 0.3077971 | 0.3084578 | 0.3290516 | 0.3290545 | 0.2895 | 0.2809 | 0.2812 | 0.2648757 | 0.2569526 | 0.2965405 | 0.3073598 |
| 1983 | 0.3152 | 0.3211 | 0.3216 | 0.3087323 | 0.3098178 | 0.3334214 | 0.3333397 | 0.2921 | 0.2817 | 0.2819 | 0.2630383 | 0.2545544 | 0.2996778 | 0.3107399 |
| 1984 | 0.3172 | 0.3238 | 0.3245 | 0.3100187 | 0.3113815 | 0.3377109 | 0.3375737 | 0.2987 | 0.2825 | 0.2827 | 0.2617423 | 0.252578 | 0.3026598 | 0.3143964 |
| 1985 | 0.3168 | 0.3265 | 0.3274 | 0.3114181 | 0.3130115 | 0.3418609 | 0.3417168 | 0.2944 | 0.2832 | 0.2835 | 0.2606173 | 0.2511214 | 0.3054096 | 0.3176265 |
| 1986 | 0.3195 | 0.3292 | 0.3302 | 0.312688 | 0.3148447 | 0.3459606 | 0.3456991 | 0.2999 | 0.284 | 0.2843 | 0.2592835 | 0.2495059 | 0.3080567 | 0.3207669 |
| 1987 | 0.3218 | 0.3319 | 0.3332 | 0.3141979 | 0.3166774 | 0.3499665 | 0.3499089 | 0.3067 | 0.2848 | 0.285 | 0.2583203 | 0.2478699 | 0.3105447 | 0.3246419 |
| 1988 | 0.3219 | 0.3346 | 0.3361 | 0.3159045 | 0.3188055 | 0.3534919 | 0.353813 | 0.308 | 0.2855 | 0.2859 | 0.2576606 | 0.2471354 | 0.3123561 | 0.3271521 |
| 1989 | 0.3278 | 0.3373 | 0.3391 | 0.3176353 | 0.3205324 | 0.3574424 | 0.3578324 | 0.3095 | 0.2863 | 0.2865 | 0.2570336 | 0.2454147 | 0.3147199 | 0.3293277 |
| 1990 | 0.3323 | 0.3401 | 0.3419 | 0.3193902 | 0.3226545 | 0.3612456 | 0.3618848 | 0.316 | 0.2871 | 0.2874 | 0.2564395 | 0.2446431 | 0.3168628 | 0.3329173 |
| 1991 | 0.3351 | 0.3428 | 0.3449 | 0.3211622 | 0.3248626 | 0.3647098 | 0.365647 | 0.3177 | 0.2879 | 0.2883 | 0.2558668 | 0.2438157 | 0.3185363 | 0.3360159 |
| 1992 | 0.339 | 0.3456 | 0.3479 | 0.3230582 | 0.3267414 | 0.3685342 | 0.3695189 | 0.3236 | 0.2887 | 0.2889 | 0.2554834 | 0.2426121 | 0.3206687 | 0.3379769 |
| 1993 | 0.3353 | 0.3483 | 0.3508 | 0.3248709 | 0.3289025 | 0.3723182 | 0.373395 | 0.3197 | 0.2895 | 0.2898 | 0.2549645 | 0.2413993 | 0.3227282 | 0.3411964 |
| 1994 | 0.3386 | 0.351 | 0.3537 | 0.3266859 | 0.3311424 | 0.3758645 | 0.3769502 | 0.3304 | 0.2902 | 0.2905 | 0.2544442 | 0.2408964 | 0.324461 | 0.3435445 |
| 1995 | 0.3397 | 0.3538 | 0.3566 | 0.3285961 | 0.3331775 | 0.3794886 | 0.3806725 | 0.3284 | 0.2909 | 0.2913 | 0.2540679 | 0.2402946 | 0.3262801 | 0.3461296 |
| 1996 | 0.3427 | 0.3565 | 0.3596 | 0.3306678 | 0.3353264 | 0.3828209 | 0.3842566 | 0.3344 | 0.2916 | 0.2921 | 0.2539389 | 0.2398858 | 0.3277102 | 0.3487171 |
| 1997 | 0.3463 | 0.3593 | 0.3625 | 0.3325665 | 0.3373944 | 0.3863456 | 0.3877663 | 0.3387 | 0.2924 | 0.293 | 0.2535346 | 0.2394905 | 0.329376 | 0.3509545 |
| 1998 | 0.3483 | 0.3621 | 0.3655 | 0.334405 | 0.3397675 | 0.3898354 | 0.3915972 | 0.3408 | 0.2932 | 0.2937 | 0.2530317 | 0.238383 | 0.3309852 | 0.3529655 |
| 1999 | 0.3478 | 0.3648 | 0.3684 | 0.3366333 | 0.3421735 | 0.3934594 | 0.3953689 | 0.3432 | 0.294 | 0.2944 | 0.2531315 | 0.2379548 | 0.3327531 | 0.3550946 |
| 2000 | 0.3507 | 0.3676 | 0.3714 | 0.338723 | 0.3444562 | 0.3969489 | 0.3992666 | 0.353 | 0.2947 | 0.2952 | 0.25301 | 0.2370732 | 0.3343395 | 0.3574583 |
| 2001 | 0.3538 | 0.3704 | 0.3743 | 0.3407647 | 0.3464839 | 0.4004086 | 0.4029681 | 0.3586 | 0.2955 | 0.2962 | 0.2528089 | 0.2369291 | 0.3358785 | 0.3600253 |
| 2002 | 0.3558 | 0.3732 | 0.3773 | 0.343043 | 0.3488584 | 0.4037736 | 0.4066951 | 0.3607 | 0.2963 | 0.2968 | 0.2529703 | 0.2365396 | 0.3372903 | 0.3617245 |
| 2003 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.3618 | 0.2971 | 0.2977 | 0.2527958 | 0.2364216 | 0.3390515 | 0.3640936 |
| Old-age dependency ratio δ2 | ||||||||||||||
| 1900 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7171 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1901 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7234 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1902 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7221 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1903 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7231 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1904 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7178 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1905 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7183 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1906 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7178 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1907 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7129 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1908 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7138 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1909 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7086 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1910 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7162 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1911 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.719 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1912 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7139 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1913 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7152 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1914 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.738 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1915 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7656 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1916 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.8138 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1917 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.857 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1918 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.9359 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1919 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7304 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1920 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7327 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1921 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7258 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1922 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7142 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1923 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7219 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1924 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7149 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1925 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7168 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1926 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.721 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1927 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7126 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1928 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7207 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1929 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7047 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1930 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7238 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1931 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7141 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1932 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7152 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1933 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7156 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1934 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7207 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1935 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7181 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1936 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.713 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1937 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7107 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1938 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7205 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1939 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7113 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1940 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.714 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1941 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7276 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1942 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7462 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1943 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.749 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1944 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7601 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1945 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7735 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1946 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.726 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1947 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7204 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1948 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7338 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1949 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7183 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1950 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7173 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1951 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7041 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1952 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.721 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1953 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7205 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1954 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7226 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1955 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7189 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1956 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7193 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1957 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7245 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1958 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.7226 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1959 | 0.7392 | . . . | . . . | . . . | . . . | . . . | . . . | 0.725 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1960 | 0.737 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7283 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1961 | 0.7414 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7226 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1962 | 0.7392 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7231 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1963 | 0.7369 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7209 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1964 | 0.7428 | . . . | . . . | . . . | . . . | . . . | . . . | 0.736 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1965 | 0.7426 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7335 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1966 | 0.7425 | . . . | . . . | . . . | . . . | . . . | . . . | 0.731 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1967 | 0.7468 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7393 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1968 | 0.7429 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7304 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1969 | 0.7481 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7307 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1970 | 0.7515 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7348 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1971 | 0.7541 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7404 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1972 | 0.753 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7343 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1973 | 0.7557 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7377 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1974 | 0.7619 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7397 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1975 | 0.7696 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7421 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1976 | 0.7711 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7389 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1977 | 0.7768 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7467 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1978 | 0.7783 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7463 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1979 | 0.7845 | . . . | . . . | . . . | . . . | . . . | . . . | 0.7461 | . . . | . . . | . . . | . . . | . . . | . . . |
| 1980 | 0.7811 | 0.7869 | 0.7864 | 0.7814854 | 0.7809068 | 0.7924609 | 0.7921503 | 0.7514 | 0.7467 | 0.7469 | 0.7407507 | 0.7312871 | 0.752853 | 0.7638705 |
| 1981 | 0.7853 | 0.7893 | 0.7892 | 0.7815495 | 0.7818693 | 0.797094 | 0.796681 | 0.7546 | 0.7472 | 0.7474 | 0.7388714 | 0.7289924 | 0.755966 | 0.7671844 |
| 1982 | 0.7879 | 0.7917 | 0.7917 | 0.7821763 | 0.7829733 | 0.8013287 | 0.8007544 | 0.7549 | 0.7478 | 0.7482 | 0.737604 | 0.726057 | 0.758623 | 0.7721451 |
| 1983 | 0.7863 | 0.7941 | 0.7944 | 0.7830131 | 0.7843666 | 0.8052991 | 0.8045971 | 0.757 | 0.7484 | 0.7488 | 0.7365677 | 0.7242651 | 0.7609688 | 0.7750479 |
| 1984 | 0.7882 | 0.7966 | 0.797 | 0.7841649 | 0.7858574 | 0.8092064 | 0.8083655 | 0.7631 | 0.7491 | 0.7495 | 0.7358515 | 0.7221234 | 0.7632336 | 0.7785212 |
| 1985 | 0.7878 | 0.799 | 0.7996 | 0.7854193 | 0.7874449 | 0.8129956 | 0.8120172 | 0.7585 | 0.7496 | 0.7502 | 0.7352399 | 0.7210678 | 0.765351 | 0.78186 |
| 1986 | 0.791 | 0.8015 | 0.8022 | 0.7865587 | 0.7890069 | 0.8167474 | 0.8157425 | 0.7637 | 0.7503 | 0.7508 | 0.7345272 | 0.7196723 | 0.7674141 | 0.784236 |
| 1987 | 0.793 | 0.8039 | 0.8049 | 0.7879147 | 0.7908195 | 0.8204213 | 0.8194734 | 0.7702 | 0.7508 | 0.7515 | 0.7340211 | 0.7181084 | 0.7693747 | 0.7877582 |
| 1988 | 0.7934 | 0.8064 | 0.8076 | 0.7894491 | 0.7927865 | 0.8236606 | 0.8229094 | 0.7713 | 0.7514 | 0.7523 | 0.7336787 | 0.7172447 | 0.7708146 | 0.7903342 |
| 1989 | 0.799 | 0.8089 | 0.8103 | 0.7910071 | 0.7945162 | 0.8272973 | 0.8266726 | 0.7724 | 0.752 | 0.7528 | 0.7333565 | 0.7161473 | 0.7727089 | 0.7922366 |
| 1990 | 0.8032 | 0.8114 | 0.8129 | 0.7925888 | 0.7963735 | 0.830805 | 0.8302687 | 0.7788 | 0.7526 | 0.7536 | 0.7330541 | 0.7149966 | 0.7744406 | 0.7953727 |
| 1991 | 0.8059 | 0.8139 | 0.8157 | 0.7941877 | 0.7984978 | 0.8340053 | 0.8337502 | 0.7801 | 0.7532 | 0.7544 | 0.7327655 | 0.7140544 | 0.7758022 | 0.7983041 |
| 1992 | 0.8093 | 0.8165 | 0.8184 | 0.7959005 | 0.8003723 | 0.8375443 | 0.837232 | 0.7854 | 0.7539 | 0.7549 | 0.7325737 | 0.7134189 | 0.7775485 | 0.8003573 |
| 1993 | 0.8061 | 0.819 | 0.8211 | 0.7975401 | 0.8024405 | 0.8410517 | 0.8408718 | 0.7815 | 0.7545 | 0.7557 | 0.732316 | 0.7120346 | 0.7792468 | 0.8030725 |
| 1994 | 0.8093 | 0.8215 | 0.8238 | 0.7991837 | 0.8043641 | 0.8443439 | 0.8440046 | 0.7917 | 0.7551 | 0.7563 | 0.73206 | 0.7118593 | 0.7806842 | 0.8054232 |
| 1995 | 0.8102 | 0.824 | 0.8265 | 0.8009154 | 0.8063554 | 0.8477133 | 0.8475714 | 0.7899 | 0.7556 | 0.757 | 0.7318763 | 0.7108363 | 0.7822015 | 0.8077975 |
| 1996 | 0.8116 | 0.8265 | 0.8292 | 0.8027959 | 0.8084903 | 0.8508158 | 0.8508444 | 0.7956 | 0.7562 | 0.7577 | 0.7318135 | 0.7101598 | 0.7834002 | 0.8098067 |
| 1997 | 0.8138 | 0.8291 | 0.832 | 0.8045215 | 0.8103601 | 0.8541018 | 0.8542466 | 0.7995 | 0.7569 | 0.7585 | 0.7316179 | 0.7100974 | 0.7848024 | 0.8121652 |
| 1998 | 0.815 | 0.8316 | 0.8347 | 0.8061942 | 0.8124763 | 0.8573596 | 0.857806 | 0.8014 | 0.7574 | 0.7592 | 0.7313765 | 0.7088505 | 0.7861633 | 0.8139408 |
| 1999 | 0.8143 | 0.8342 | 0.8374 | 0.8082239 | 0.8146104 | 0.8607472 | 0.8611384 | 0.8036 | 0.7581 | 0.7598 | 0.7314275 | 0.7088786 | 0.787665 | 0.815943 |
| 2000 | 0.8173 | 0.8368 | 0.8402 | 0.8101297 | 0.8167252 | 0.8640133 | 0.8647204 | 0.8131 | 0.7587 | 0.7605 | 0.7313688 | 0.7080973 | 0.7890186 | 0.8182765 |
| 2001 | 0.8206 | 0.8394 | 0.8429 | 0.8119938 | 0.8187642 | 0.8672555 | 0.8682446 | 0.8184 | 0.7593 | 0.7614 | 0.7312731 | 0.7076554 | 0.7903369 | 0.8208523 |
| 2002 | 0.8226 | 0.8419 | 0.8457 | 0.8140766 | 0.8210406 | 0.8704127 | 0.8717245 | 0.8202 | 0.7599 | 0.7619 | 0.7313472 | 0.7071208 | 0.7915506 | 0.8224514 |
| 2003 | . . . | . . . | . . . | . . . | . . . | . . . | . . . | 0.8212 | 0.7605 | 0.7628 | 0.7312645 | 0.7069049 | 0.7930705 | 0.8251649 |
The experimental design of the ex-post analysis implemented in this paper looks at forecast error at fixed lead times, using different forecast origins. For every data set and model, N = 20,000 random paths are simulated from 1980 forward for each of the 21 age groups. Since the Lee-Carter model takes as inputs the logarithmic death rates while the AR(1) approach models the rates of mortality improvement, the generated paths are transformed back into mortality rates prior to computing the features of interest of the forecast distribution. The mortality paths are then used to calculate the mean, median, and 5th and 95th quantiles for each age group and forecast period. In addition, the simulations corresponding to all 21 ages are also used to compute similar estimates for life expectancy at birth and the dependency ratios and . Finally, the same process is repeated with other jump-off years (1981, 1982, 1983 and so on). This is done to limit the influence of any particular forecast origin on the results, and thus, improve the robustness of the findings. At the end of the exercise, there are n projections of the quantities of interest with a 1-year forecast horizon, n − 1 projections 2 years ahead, and eventually, 1 projection n years into the future, where n denotes the longest forecast horizon available, as the fourth column of Table 1 shows.
Once all the projections are obtained it is a simple matter to evaluate forecast error using the specified performance criteria. For the point estimators (means and medians), performance is measured in terms of RMSE. Formally, let represent the Δt-step-ahead forecast of the mortality rate for age group a in year t. The RMSE associated with a particular age series and fixed lead time Δt is calculated as follows:
where ti represents the jump-off year of the forecast in question and denotes observed mortality. For instance, taking a 1-year forecast horizon (Δt = 1), for the United States (see Table 1) there are 23 forecasts spanning the period from ti = 1980 to T = 2002. Similarly, there are 14 ten-step-ahead forecasts (Δt = 10), with ti = 1989 and T = 2002, while the single 23-years-ahead projection involves ti = T = 2002.
The performance of the interval forecasts is determined by computing the actual fraction of times ex-post mortality rates lie inside the intervals. Let denote the area covered by the 90 percent Δt-step-ahead interval forecast of mortality for age-group a in year t. Furthermore, define an indicator function taking a value of 1 if the calculated includes the observed mortality rate, and 0 otherwise:
Then, the empirical probability associated with the interval projection at age a and forecast horizon Δt is given by
A similar approach is used to calculate the average width of the intervals.
Finally, the overall measures of performance are a function of either all or most of the 21 age groups. In this case, the forecast error associated with the point estimates of the entire age profile at a particular forecast horizon Δt is simply obtained by averaging over the ages
Likewise, the RMSE associated with, for instance, the point projections of life expectancy at birth and forecast horizon Δt is computed as follows
Similar expressions for the dependency ratios are obtained by replacing and above with the corresponding values of and . The extension of these equations to compute the empirical coverage and average width of the interval estimates is also obvious. In addition, it is straightforward to modify these expressions to estimate forecast error over multiple forecast horizons or the entire forecast period.
Forecast Performance of Point Projections
The first four columns of Table 4 present the resulting RMSE corresponding to the median forecasts of the Lee-Carter (LC) model for the following measures of overall forecast performance: the age profile, life expectancy at birth e0, and the two age-dependency ratios δ1 and δ2 defined in equations (25) and (26), respectively. These quantities are computed over all available forecast horizons. Since both the means and medians of the forecast distribution are entertained as plausible point estimators, columns 5 through 8 in Table 4 display the ratio of RMSE between the two. Clearly, for the first three measures (the age profile, e0, and δ1), the median is a better performing point estimator than the mean in the large majority of cases, as most of the ratios exceed 1. Only for the more comprehensive measure of dependency (δ2) do the mean projections generally exhibit lower RMSE than their median counterpart, although the differences between the two are fairly small. Moreover, while not shown for the sake of conciseness, the results corresponding to the AR(1) model are qualitatively similar. In light of these findings, this paper focuses exclusively on the median forecasts from this point forward.
| Country | LC: RMSE of median forecasts | LC: Ratio of RMSE (mean/median) | ||||||
|---|---|---|---|---|---|---|---|---|
| Age Profile | e0 | δ1 | δ2 | Age Profile | e0 | δ1 | δ2 | |
| Austria | 0.01270 | 1.55660 | 0.03082 | 0.02887 | 1.006 | 1.057 | 1.005 | 0.996 |
| Belgium | 0.00787 | 1.08555 | 0.02921 | 0.03067 | 1.020 | 1.168 | 1.007 | 0.979 |
| Canada | 0.00422 | 0.91612 | 0.01810 | 0.01684 | 1.001 | 1.024 | 1.002 | 0.996 |
| Denmark | 0.00693 | 0.85787 | 0.01476 | 0.01346 | 1.004 | 1.124 | 1.020 | 0.982 |
| Finland | 0.00977 | 1.46775 | 0.03279 | 0.03256 | 1.005 | 1.147 | 1.009 | 0.972 |
| France | 0.00803 | 1.22205 | 0.02809 | 0.02854 | 1.081 | 1.367 | 1.024 | 0.928 |
| Germany | 0.00801 | 1.65540 | 0.02827 | 0.02494 | 1.021 | 1.031 | 0.997 | 0.993 |
| Italy | 0.01469 | 1.89066 | 0.03745 | 0.03691 | 1.007 | 1.094 | 1.013 | 0.992 |
| Japan | 0.01434 | 0.40010 | 0.01164 | 0.01453 | 1.003 | 0.962 | 1.016 | 1.007 |
| Netherlands | 0.00687 | 0.45293 | 0.01030 | 0.01043 | 0.995 | 1.541 | 1.056 | 0.954 |
| Norway | 0.00972 | 1.26707 | 0.02499 | 0.02474 | 1.001 | 1.083 | 1.011 | 0.990 |
| Spain | 0.00703 | 0.41821 | 0.01380 | 0.01659 | 1.010 | 1.342 | 1.060 | 1.006 |
| Sweden | 0.00698 | 1.90267 | 0.03206 | 0.02914 | 1.025 | 1.144 | 1.034 | 0.992 |
| Switzerland | 0.00662 | 1.19000 | 0.02600 | 0.02568 | 1.024 | 1.096 | 1.018 | 0.996 |
| United Kingdom | 0.00851 | 1.90517 | 0.03731 | 0.03622 | 1.011 | 1.107 | 1.012 | 0.987 |
| United States | 0.00854 | 0.31685 | 0.00782 | 0.00861 | 0.991 | 0.981 | 1.002 | 1.006 |
| SOURCE: Author's calculations | ||||||||
| NOTES: LC = Lee-Carter Model; RMSE = root mean squared error. | ||||||||
To facilitate comparison, columns 1 through 4 in Table 5 present the ratios of RMSE in the median forecasts between the LC and AR(1) models (again, over all forecast horizons). Notice how forecast performance can vary across the different specified criteria. For example, for the Netherlands or the United States, the AR(1) approach outperforms Lee-Carter over the age profile, while the latter model actually exhibits lower RMSE for the projections of life expectancy and the dependency ratios. Conversely, for Finland, Germany and Japan, the LC model enjoys lower RMSE over the age profile but is outranked by the first-order autoregressive approach in the remaining measures.
| Country | Ratio of RMSE AR(1)/LC | LC: Below actual (percent) | AR(1): Below actual (percent) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age Profile | e0 | δ1 | δ2 | Age Profile | e0 | δ1 | δ2 | Age Profile | e0 | δ1 | δ2 | |
| Austria | 1.224 | 1.194 | 1.141 | 1.125 | 22.89 | 96.59 | 97.85 | 98.28 | 20.11 | 98.60 | 99.81 | 99.43 |
| Belgium | 0.918 | 0.979 | 0.911 | 0.865 | 49.87 | 95.39 | 97.49 | 97.49 | 48.67 | 97.40 | 98.26 | 98.26 |
| Canada | 0.988 | 0.997 | 0.970 | 0.956 | 31.26 | 96.11 | 96.52 | 96.75 | 27.45 | 96.32 | 97.21 | 96.77 |
| Denmark | 1.045 | 1.124 | 1.020 | 0.965 | 41.88 | 79.01 | 79.96 | 81.49 | 41.38 | 83.15 | 81.12 | 80.90 |
| Finland | 1.045 | 0.954 | 0.947 | 0.848 | 41.88 | 93.24 | 96.76 | 98.07 | 41.38 | 93.77 | 98.81 | 98.83 |
| France | 0.901 | 0.574 | 0.893 | 0.818 | 33.29 | 97.07 | 97.46 | 97.44 | 37.10 | 98.62 | 98.84 | 95.23 |
| Germany | 1.013 | 0.933 | 0.937 | 0.944 | 15.40 | 98.03 | 98.64 | 98.25 | 15.06 | 98.41 | 99.03 | 99.05 |
| Italy | 0.985 | 0.992 | 1.020 | 1.005 | 32.26 | 98.47 | 98.63 | 98.44 | 36.54 | 99.05 | 98.82 | 98.82 |
| Japan | 1.002 | 0.845 | 0.985 | 0.969 | 71.89 | 20.47 | 78.85 | 85.70 | 70.50 | 29.67 | 83.37 | 87.07 |
| Netherlands | 0.943 | 1.450 | 1.234 | 1.136 | 46.25 | 89.57 | 92.00 | 92.82 | 42.21 | 95.47 | 95.92 | 96.38 |
| Norway | 0.914 | 0.978 | 0.924 | 0.900 | 33.79 | 89.76 | 93.63 | 95.51 | 33.76 | 90.33 | 93.62 | 94.86 |
| Spain | 0.964 | 0.923 | 0.888 | 0.849 | 51.62 | 72.22 | 92.69 | 94.72 | 53.05 | 71.30 | 93.35 | 94.31 |
| Sweden | 1.154 | 1.181 | 1.159 | 1.132 | 11.44 | 98.56 | 98.04 | 97.66 | 10.77 | 99.65 | 99.65 | 99.48 |
| Switzerland | 1.102 | 1.044 | 1.023 | 0.982 | 31.32 | 95.46 | 98.04 | 98.20 | 30.38 | 96.83 | 98.36 | 98.53 |
| United Kingdom | 1.023 | 1.114 | 1.035 | 0.989 | 29.33 | 99.12 | 99.12 | 98.94 | 25.92 | 99.65 | 99.65 | 99.65 |
| United States | 0.970 | 1.413 | 1.235 | 1.191 | 50.41 | 33.07 | 19.01 | 17.79 | 54.86 | 24.64 | 13.05 | 11.82 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag 1 autoregression; LC = Lee-Carter Model. | ||||||||||||
The LC model outranks the autoregressive approach in half of all cases for δ1 and the age profile, while the AR(1) model displays lower RMSE in the other half. For life expectancy at birth e0, the LC model does better in 7 of the data sets but is outperformed in the remaining 9 cases. For the broader dependency measure δ2, the AR(1) approach outperforms the LC model in 11 out of the 16 countries. Furthermore, in most instances, the differences in performance between the models are relatively small (that is, most of the ratios are fairly close to 1). There are a few notable exceptions to this finding for the forecasts of e0. For instance, for France, the AR(1) approach reduces forecast error in life expectancy at birth by almost half relative to the LC model-likewise for the Netherlands and the United States. Overall, however, both models seem to display rather similar performance.
The remaining columns in Table 5 report the percentage of times the median projections in both models fall below the actual values for each of the four evaluation criteria. Clearly, for a given measure, the percentages corresponding to each model are very close to one another, suggesting that both models generate forecasts that are roughly biased in the same direction. With the exceptions of Japan, Spain, and the United States, notice that over the age profile, the percentages in Table 5 fall below 50 percent, so that the models tend to moderately overestimate actual mortality in most cases. By contrast, the large majority of the forecasts of life expectancy at birth and the age-dependency ratios underestimate their observed values. Specifically, only the median projections corresponding to Japan and the United States overpredict life expectancy, while the dependency ratios are also overestimated only for the United States. For the remaining data sets, between 70 percent to 99 percent of all generated forecasts underpredict e0, δ1, and δ2.
To gain insight into the results presented in Table 5 (the models' forecasts overestimate actual mortality but underestimate life expectancy and the age dependency ratios), it is important to consider the mechanism via which the age-specific mortalities enter the calculation of e0, δ1, and δ2. In all cases, the quantities that matter are the longitudinal numbers of survivors out of some initial population, as defined in equation (21). Suppose that a particular forecast overpredicts actual mortality at age a and time t. Then, the implied survival rate will underestimate the projected number of people that graduate into the next age category. Of course, whether the resulting future estimates of life expectancy at birth will underproject the observed values depends not only on the fraction of the age-specific rates that overestimate mortality, but also on the magnitude of their forecast error. Dependency ratios are further complicated by the fact that they comprise the quotient of longitudinal numbers of survivors at different ages, so that the distribution of both the bias and magnitude of forecast error across the ages plays a large role.
Performance by Age Group
One way to measure how error is distributed among the ages is to determine the percentage that each particular age group contributes to the value of total forecast error. For ease of presentation and to maintain consistency with how the dependency ratios have been defined, the individual age groups are aggregated into three broad categories (ages 0–19, ages 2–64, and ages 65–95 or older, respectively), containing 5, 9, and 7 of the 21 original groups. Broadly, these three categories encompass birth to young adulthood, the working population, and individuals in retirement ages. Following the discussion in the previous section, the RMSE associated with some individual age group a over all forecast horizons Δt is determined by
where n denotes the longest forecast horizon shown in Table 1. Similarly, the computation of RMSE over the entire age profile involves
with aj representing either a single age group or a subset of ages, such as the 65–95 or older retirement category. It follows then, that the proportion pi of total mean squared error (MSE) corresponding to aj is given by
Table 6 displays the percentage of forecast error over the entire age profile that is attributed to two broad sets of ages. The first set comprises the initial 14 age groups being modeled (from birth to age 64). These series make up less than 1 percent of total forecast error in most cases, and less than 3 percent in both models and all 16 data sets. By contrast, the retirement ages account for 97 percent to 99 percent of total MSE. In terms of model performance by age, the first three columns in Table 7 present the ratio of RMSE between models for the three broad age categories specified by the dependency measures. The first-order autoregressive approach outperforms the Lee-Carter model in 11 out of the 16 countries for the youngest age groups (ages 0–19), 7 countries for the working population (ages 20–64), and half of all countries for the retirement category (ages 65–95 or older). Furthermore, a comparison of the ratios in the first column of Table 5 with those in the third column of Table 7 reveals that they are virtually identical in magnitude, confirming once more that the oldest age groups overwhelmingly determine total forecast error over the age profile. The remaining columns in Table 7 show the percentage of the median forecasts that fall below the observed ex-post mortality rates by model and broad age category. Clearly, in all but one case (the United States), the models are far more likely to overestimate actual mortality for the oldest ages than for any age group. In most cases, over three-fourths of the generated projections for the 65–95 or older ages overpredict observed mortality.
| Country | Ages 0–64 | Ages 65–95 or Older | ||
|---|---|---|---|---|
| LC | AR(1) | LC | AR(1) | |
| Austria | 0.13 | 0.12 | 99.87 | 99.88 |
| Belgium | 0.63 | 0.64 | 99.37 | 99.36 |
| Canada | 2.24 | 2.12 | 97.76 | 97.88 |
| Denmark | 0.70 | 0.66 | 99.30 | 99.34 |
| Finland | 0.70 | 0.58 | 99.30 | 99.42 |
| France | 0.38 | 0.42 | 99.62 | 99.58 |
| Germany | 0.29 | 0.28 | 99.71 | 99.72 |
| Italy | 0.39 | 0.38 | 99.61 | 99.62 |
| Japan | 0.15 | 0.12 | 99.85 | 99.88 |
| Netherlands | 0.25 | 0.35 | 99.75 | 99.65 |
| Norway | 0.53 | 0.54 | 99.47 | 99.46 |
| Spain | 0.35 | 0.26 | 99.65 | 99.74 |
| Sweden | 0.90 | 0.82 | 99.10 | 99.18 |
| Switzerland | 0.33 | 0.30 | 99.67 | 99.70 |
| United Kingdom | 1.57 | 1.65 | 98.43 | 98.35 |
| United States | 0.09 | 0.13 | 99.91 | 99.87 |
| SOURCE: Author's calculations | ||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||
| Country | Ratio of RMSE AR(1)/LC | Ages 0–19 | Ages 20–64 | Ages 65–95 or older | |||||
|---|---|---|---|---|---|---|---|---|---|
| Ages 0–19 | Ages 20–64 | Ages 65–95 or older |
LC | AR(1) | LC | AR(1) | LC | AR(1) | |
| Austria | 1.131 | 1.195 | 1.224 | 49.62 | 41.63 | 20.36 | 20.65 | 7.05 | 4.04 |
| Belgium | 0.916 | 0.926 | 0.918 | 67.82 | 64.29 | 68.22 | 66.29 | 13.45 | 14.86 |
| Canada | 1.166 | 0.951 | 0.989 | 52.79 | 50.86 | 39.59 | 39.17 | 37.03 | 37.47 |
| Denmark | 0.883 | 1.038 | 1.045 | 36.77 | 31.71 | 33.17 | 29.38 | 24.87 | 21.92 |
| Finland | 0.968 | 0.949 | 1.045 | 62.47 | 55.50 | 50.01 | 52.48 | 21.47 | 18.23 |
| France | 0.624 | 1.019 | 0.901 | 31.56 | 44.02 | 54.50 | 56.21 | 7.25 | 7.60 |
| Germany | 1.093 | 0.989 | 1.013 | 23.09 | 19.42 | 15.46 | 17.43 | 9.84 | 8.91 |
| Italy | 0.930 | 1.001 | 0.986 | 52.51 | 62.96 | 43.17 | 47.96 | 3.76 | 2.99 |
| Japan | 0.893 | 0.935 | 1.002 | 96.34 | 95.64 | 96.28 | 94.31 | 23.07 | 21.91 |
| Netherlands | 0.989 | 1.130 | 0.942 | 38.87 | 36.90 | 58.71 | 54.69 | 35.51 | 29.96 |
| Norway | 0.916 | 0.923 | 0.914 | 31.99 | 33.28 | 48.26 | 47.36 | 16.48 | 16.62 |
| Spain | 0.720 | 1.039 | 0.964 | 68.86 | 68.63 | 71.87 | 74.11 | 13.29 | 14.84 |
| Sweden | 0.929 | 1.152 | 1.154 | 18.29 | 19.60 | 8.14 | 7.54 | 10.79 | 8.60 |
| Switzerland | 1.055 | 1.054 | 1.102 | 37.51 | 39.30 | 42.81 | 44.39 | 12.12 | 6.00 |
| United Kingdom | 0.995 | 1.060 | 1.023 | 19.85 | 15.40 | 52.39 | 48.32 | 6.45 | 4.64 |
| United States | 1.515 | 0.983 | 0.969 | 28.35 | 36.11 | 42.40 | 43.60 | 76.47 | 82.75 |
| SOURCE: Author's calculations | |||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag autoregression; LC = Lee-Carter Model. | |||||||||
Two obvious patterns concerning the models' median forecasts emerge from Tables 6 and 7. First, the bulk of forecast error is heavily concentrated among the oldest ages. Second, the majority of the forecasts corresponding to these age groups overestimate observed mortality. These findings shed additional light on the results shown previously in Table 5. In particular, a very high proportion of the forecasts for the 65–95 or older age groups overestimates mortality and hence, underestimates the number of population survivors at these ages. Furthermore, since these groups carry greater importance in determining how the magnitude of the forecast error is distributed across the ages, they are more likely to underpredict the total number of person-years remaining at birth, and thus e0. Similarly, the 65–95 or older age groups enter the computation of the dependency ratios through the numerator. Consequently, if the number of survivors at these ages is underestimated, so are likely to be the values of δ1 and δ2. The exception to this pattern involves the projections for the United States, where mortality is underestimated at the oldest ages instead, while the forecasts of life expectancy and the dependency ratios overestimate their ex-post values.
Performance by Forecast Horizon
To assess how the median forecasts change with the length of the forecast horizon, the generated projections are grouped into four periods: 1–5 years, 6–10 years, 11–15 years, and 16 or more years ahead. Notice that the last category varies with the final year of data available for each series, involving 16–23 years ahead in most cases. Table 8 presents the ratio of RMSE between models over the age profile, as well as the percentage of the median forecasts that fall below observed ex-post mortality over the various forecast horizons. Tables 9 through 11 display similar quantities for the projections of life expectancy at birth e0 and the dependency ratios δ1 and δ2, respectively. Although not discernible from the ratios in the first four columns of each table, as expected, forecast error generally increases with the distance of the forecast horizon.
| Country | Ratio of RMSE AR(1)/LC | LC: Below actual (percent | AR(1): Below actual (percent) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 1.015 | 1.160 | 1.213 | 1.249 | 36.04 | 22.50 | 19.01 | 17.35 | 32.90 | 20.87 | 16.97 | 13.60 |
| Belgium | 0.930 | 0.953 | 0.973 | 0.874 | 49.92 | 51.35 | 51.15 | 48.12 | 45.98 | 49.55 | 50.54 | 48.64 |
| Canada | 0.883 | 0.874 | 0.953 | 1.049 | 38.74 | 41.61 | 46.97 | 40.83 | 37.84 | 40.27 | 45.58 | 41.68 |
| Denmark | 1.026 | 1.030 | 0.995 | 1.066 | 42.69 | 38.49 | 32.35 | 21.39 | 39.69 | 35.89 | 28.51 | 16.57 |
| Finland | 1.011 | 0.952 | 0.955 | 1.125 | 40.89 | 40.62 | 44.74 | 46.05 | 34.87 | 40.26 | 45.03 | 45.03 |
| France | 0.962 | 0.953 | 0.918 | 0.878 | 40.35 | 30.76 | 30.72 | 32.05 | 39.22 | 39.70 | 35.96 | 34.87 |
| Germany | 0.996 | 1.004 | 1.000 | 1.019 | 28.56 | 22.03 | 12.37 | 4.93 | 28.42 | 23.76 | 13.97 | 1.97 |
| Italy | 1.019 | 1.003 | 0.988 | 0.981 | 30.70 | 28.21 | 36.82 | 32.91 | 28.30 | 31.83 | 41.83 | 41.33 |
| Japan | 0.996 | 1.033 | 1.023 | 0.995 | 68.01 | 72.06 | 74.11 | 72.83 | 63.03 | 70.47 | 74.26 | 72.83 |
| Netherlands | 0.972 | 0.915 | 0.948 | 0.940 | 46.13 | 44.90 | 47.38 | 46.44 | 38.24 | 41.38 | 44.61 | 43.55 |
| Norway | 0.932 | 0.954 | 0.905 | 0.874 | 43.42 | 36.34 | 30.18 | 28.45 | 41.93 | 37.17 | 29.41 | 29.25 |
| Spain | 0.959 | 0.978 | 0.954 | 0.965 | 50.42 | 47.47 | 51.81 | 54.50 | 47.68 | 51.39 | 55.12 | 55.81 |
| Sweden | 1.080 | 1.076 | 1.133 | 1.186 | 27.30 | 13.88 | 6.14 | 4.22 | 21.02 | 12.46 | 6.75 | 6.36 |
| Switzerland | 1.056 | 1.077 | 1.079 | 1.115 | 38.76 | 30.11 | 29.34 | 29.19 | 34.45 | 29.13 | 28.73 | 29.81 |
| United Kingdom | 0.968 | 1.010 | 1.026 | 1.027 | 36.26 | 31.89 | 27.75 | 24.94 | 30.11 | 29.22 | 25.87 | 21.79 |
| United States | 0.975 | 0.961 | 0.962 | 0.972 | 51.02 | 50.57 | 50.56 | 49.84 | 54.09 | 55.28 | 57.03 | 53.74 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag autoregression; LC = Lee-Carter Model. | ||||||||||||
Beginning with the age profile in Table 8, the first-order autoregressive approach outperforms the Lee-Carter model in ten cases for the 1–5 and 11–15 year horizons and in eight cases for the 6–10 and 16 or more year periods. While not always true, the differences in model performance tend to increase with the length of the forecast horizon, with the largest divergence corresponding to Austria in the 16 or more year period, where RMSE over the age profile for the AR(1) model is approximately 25 percent greater than for the LC approach. In most cases, a moderately larger proportion of the mortality forecasts tend to overpredict their observed values, except for Japan, where roughly three-fourths of the mortality forecasts involve underpredictions. The same pattern holds true for Spain and the United States, where approximately 50 percent of all forecasts underpredict mortality. Moreover, in about half of all countries, the percentage of projections overpredicting mortality increases as a function of the forecast horizon.
Turning to the median projections of life expectancy at birth in Table 9, the LC model outperforms the AR(1) approach in thirteen countries for the 1–5 year horizon, nine countries for the 6–10 year period, eight countries for the 11–15 horizon, and seven countries for 16 or more years ahead. Barring a few exceptions typically involving the longest forecast horizons (such as France, the Netherlands, and the United States), most of these ratios are relatively close to 1. Moreover, excluding the United States and Japan, the projections generated by both models overwhelmingly underpredict life expectancy, particularly as the distance of the forecast horizon increases. In fact, at the 16 or more year horizon 100 percent of the forecasts of life expectancy at birth underpredict their ex-post values for the majority of the data sets in both models.
| Country | Ratio of RMSE AR(1)/LC | LC: Below actual (percent | AR(1): Below actual (percent) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 1.169 | 1.194 | 1.198 | 1.193 | 84.32 | 100.00 | 100.00 | 100.00 | 93.58 | 100.00 | 100.00 | 100.00 |
| Belgium | 1.057 | 1.004 | 0.982 | 0.974 | 78.80 | 100.00 | 100.00 | 100.00 | 88.06 | 100.00 | 100.00 | 100.00 |
| Canada | 1.024 | 1.012 | 1.005 | 0.994 | 82.10 | 100.00 | 100.00 | 100.00 | 83.05 | 100.00 | 100.00 | 100.00 |
| Denmark | 1.102 | 1.082 | 1.106 | 1.139 | 62.42 | 61.24 | 75.61 | 97.89 | 68.76 | 71.10 | 80.13 | 97.89 |
| Finland | 1.068 | 0.977 | 0.938 | 0.952 | 78.36 | 90.55 | 100.00 | 100.00 | 80.78 | 90.55 | 100.00 | 100.00 |
| France | 0.800 | 0.468 | 0.516 | 0.595 | 86.54 | 100.00 | 100.00 | 100.00 | 95.94 | 97.71 | 100.00 | 100.00 |
| Germany | 0.977 | 0.954 | 0.929 | 0.931 | 90.93 | 100.00 | 100.00 | 100.00 | 92.67 | 100.00 | 100.00 | 100.00 |
| Italy | 1.025 | 0.981 | 0.981 | 0.995 | 92.96 | 100.00 | 100.00 | 100.00 | 95.61 | 100.00 | 100.00 | 100.00 |
| Japan | 0.907 | 0.842 | 0.795 | 0.901 | 36.63 | 17.32 | 1.54 | 24.18 | 48.30 | 29.91 | 5.76 | 32.83 |
| Netherlands | 1.193 | 1.344 | 1.479 | 1.471 | 69.87 | 86.15 | 93.94 | 100.00 | 83.07 | 95.19 | 100.00 | 100.00 |
| Norway | 1.020 | 0.998 | 0.980 | 0.971 | 73.60 | 79.31 | 100.00 | 100.00 | 76.21 | 79.31 | 100.00 | 100.00 |
| Spain | 1.022 | 0.972 | 0.912 | 0.898 | 55.74 | 58.69 | 64.17 | 93.36 | 61.03 | 57.30 | 60.93 | 90.54 |
| Sweden | 1.225 | 1.192 | 1.179 | 1.180 | 93.07 | 100.00 | 100.00 | 100.00 | 98.33 | 100.00 | 100.00 | 100.00 |
| Switzerland | 1.083 | 1.048 | 1.035 | 1.044 | 80.33 | 96.95 | 100.00 | 100.00 | 86.14 | 98.00 | 100.00 | 100.00 |
| United Kingdom | 1.151 | 1.127 | 1.115 | 1.113 | 95.80 | 100.00 | 100.00 | 100.00 | 98.33 | 100.00 | 100.00 | 100.00 |
| United States | 1.097 | 1.255 | 1.390 | 1.525 | 43.78 | 36.78 | 37.23 | 21.47 | 38.04 | 33.15 | 33.47 | 5.43 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag autoregression; LC = Lee-Carter Model. | ||||||||||||
Finally, Tables 10 and 11 show the performance of the point projections of the dependency ratios. For the δ1 ratio (survivors at ages 65–95 or older over ages 20–64), the LC model outperforms the AR(1) approach in ten cases for the 1–5 and 6–10 year horizons, nine cases for the 11–15 year period and eight cases for 16 or more years ahead. On the other hand, for the broader measure of dependency δ2 (ages 0–19 and 65–95 or older over 20–64), the LC approach outranks the autoregressive model in ten cases for the 1–5 year forecast period, six cases for the 6–10 year horizon, and only five cases for 11–15 and 16 or more years ahead. For both measures of dependency and all sixteen data sets, the largest difference in performance between the models does not exceed 26 percent at any forecast horizon. In all but one instance (the United States), the median projections of both dependency ratios underestimate their observed values increasingly as a function of the forecast period. At the 16 or more year horizon, virtually all of the generated forecasts underestimate the observed dependency values, while the converse is also true for the U.S. data (none of the median projections fall below the corresponding ex-post quantities).
| Country | Ratio of RMSE AR(1)/LC | LC: Below actual (percent | AR(1): Below actual (percent) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 1.182 | 1.170 | 1.158 | 1.134 | 90.10 | 100.00 | 100.00 | 100.00 | 99.13 | 100.00 | 100.00 | 100.00 |
| Belgium | 0.964 | 0.924 | 0.913 | 0.908 | 88.46 | 100.00 | 100.00 | 100.00 | 92.02 | 100.00 | 100.00 | 100.00 |
| Canada | 1.022 | 1.001 | 0.993 | 0.961 | 85.11 | 98.89 | 100.00 | 100.00 | 87.15 | 100.00 | 100.00 | 100.00 |
| Denmark | 1.065 | 1.030 | 1.023 | 1.015 | 65.15 | 63.16 | 75.70 | 97.89 | 67.70 | 66.52 | 75.59 | 97.89 |
| Finland | 1.005 | 0.958 | 0.941 | 0.945 | 86.23 | 98.89 | 100.00 | 100.00 | 94.53 | 100.00 | 100.00 | 100.00 |
| France | 0.989 | 0.927 | 0.902 | 0.884 | 88.32 | 100.00 | 100.00 | 100.00 | 94.66 | 100.00 | 100.00 | 100.00 |
| Germany | 0.987 | 0.960 | 0.947 | 0.932 | 93.75 | 100.00 | 100.00 | 100.00 | 95.53 | 100.00 | 100.00 | 100.00 |
| Italy | 1.026 | 1.008 | 1.012 | 1.023 | 93.70 | 100.00 | 100.00 | 100.00 | 94.57 | 100.00 | 100.00 | 100.00 |
| Japan | 0.998 | 1.024 | 1.054 | 0.974 | 61.45 | 67.19 | 74.09 | 100.00 | 67.91 | 72.54 | 83.06 | 100.00 |
| Netherlands | 1.138 | 1.181 | 1.241 | 1.243 | 72.49 | 90.54 | 98.57 | 100.00 | 84.07 | 96.36 | 100.00 | 100.00 |
| Norway | 0.970 | 0.946 | 0.925 | 0.919 | 77.61 | 93.06 | 100.00 | 100.00 | 81.05 | 89.60 | 100.00 | 100.00 |
| Spain | 0.966 | 0.880 | 0.867 | 0.891 | 72.71 | 92.19 | 100.00 | 100.00 | 75.24 | 94.36 | 98.46 | 100.00 |
| Sweden | 1.198 | 1.167 | 1.156 | 1.158 | 90.61 | 100.00 | 100.00 | 100.00 | 98.33 | 100.00 | 100.00 | 100.00 |
| Switzerland | 1.064 | 1.036 | 1.021 | 1.022 | 90.20 | 100.00 | 100.00 | 100.00 | 91.80 | 100.00 | 100.00 | 100.00 |
| United Kingdom | 1.070 | 1.040 | 1.033 | 1.035 | 95.80 | 100.00 | 100.00 | 100.00 | 98.33 | 100.00 | 100.00 | 100.00 |
| United States | 1.042 | 1.146 | 1.240 | 1.252 | 40.36 | 28.64 | 18.46 | 0.00 | 36.55 | 14.80 | 8.69 | 0.00 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag autoregression; LC = Lee-Carter Model. | ||||||||||||
| Country | Ratio of RMSE AR(1)/LC | LC: Below actual (percent | AR(1): Below actual (percent) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 1.192 | 1.170 | 1.150 | 1.115 | 92.10 | 100.00 | 100.00 | 100.00 | 97.39 | 100.00 | 100.00 | 100.00 |
| Belgium | 0.915 | 0.877 | 0.870 | 0.861 | 88.46 | 100.00 | 100.00 | 100.00 | 92.02 | 100.00 | 100.00 | 100.00 |
| Canada | 1.020 | 0.995 | 0.986 | 0.944 | 86.15 | 98.89 | 100.00 | 100.00 | 86.28 | 98.89 | 100.00 | 100.00 |
| Denmark | 1.051 | 1.009 | 0.983 | 0.948 | 68.00 | 66.64 | 77.03 | 97.89 | 67.89 | 66.66 | 74.16 | 97.89 |
| Finland | 0.901 | 0.846 | 0.836 | 0.851 | 91.14 | 100.00 | 100.00 | 100.00 | 94.62 | 100.00 | 100.00 | 100.00 |
| France | 0.805 | 0.800 | 0.817 | 0.821 | 88.22 | 100.00 | 100.00 | 100.00 | 80.34 | 97.71 | 100.00 | 100.00 |
| Germany | 0.996 | 0.968 | 0.960 | 0.938 | 91.97 | 100.00 | 100.00 | 100.00 | 95.61 | 100.00 | 100.00 | 100.00 |
| Italy | 1.007 | 0.993 | 0.998 | 1.008 | 92.83 | 100.00 | 100.00 | 100.00 | 94.57 | 100.00 | 100.00 | 100.00 |
| Japan | 1.002 | 1.027 | 1.020 | 0.957 | 68.74 | 73.58 | 91.90 | 100.00 | 68.78 | 79.85 | 91.90 | 100.00 |
| Netherlands | 1.101 | 1.103 | 1.136 | 1.140 | 71.61 | 93.94 | 100.00 | 100.00 | 84.94 | 97.70 | 100.00 | 100.00 |
| Norway | 0.947 | 0.920 | 0.900 | 0.896 | 81.57 | 97.78 | 100.00 | 100.00 | 82.13 | 94.24 | 100.00 | 100.00 |
| Spain | 0.924 | 0.848 | 0.834 | 0.851 | 78.92 | 95.73 | 100.00 | 100.00 | 80.50 | 92.19 | 100.00 | 100.00 |
| Sweden | 1.172 | 1.141 | 1.130 | 1.131 | 88.78 | 100.00 | 100.00 | 100.00 | 97.50 | 100.00 | 100.00 | 100.00 |
| Switzerland | 1.018 | 0.985 | 0.974 | 0.983 | 91.00 | 100.00 | 100.00 | 100.00 | 92.63 | 100.00 | 100.00 | 100.00 |
| United Kingdom | 1.032 | 0.994 | 0.988 | 0.989 | 94.93 | 100.00 | 100.00 | 100.00 | 98.33 | 100.00 | 100.00 | 100.00 |
| United States | 1.015 | 1.134 | 1.237 | 1.199 | 32.64 | 33.92 | 15.25 | 0.00 | 29.81 | 24.55 | 0.00 | 0.00 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: RMSE = root mean squared error; AR(1) = Lag autoregression; LC = Lee-Carter Model. | ||||||||||||
Forecast Performance of Interval Projections
The first two columns in Table 12 display the empirical probability content of the 90-percent forecast confidence intervals generated by the models for the age profile, over all forecast horizons. The third and fourth columns in the same table respectively present the average width of these intervals for the Lee-Carter model, and the ratio of average width between models. The last four columns in Table 12 show similar quantities for life expectancy at birth e0, while Table 13 displays analogous coverage and width measures for the two age dependency ratios δ1 and δ2.
| Country | Age profile | Life expectancy at birth | ||||||
|---|---|---|---|---|---|---|---|---|
| Empirical coverage (percent) | Average width | Empirical coverage (percent) | Average width | |||||
| LC | AR(1) | LC | AR(1)/LC | LC | AR(1) | LC | AR(1)/LC | |
| Austria | 66.02 | 74.43 | 0.006 | 3.559 | 71.66 | 24.58 | 3.666 | 0.544 |
| Belgium | 81.97 | 89.05 | 0.011 | 2.831 | 100.00 | 100.00 | 5.287 | 0.839 |
| Canada | 63.56 | 82.01 | 0.003 | 4.648 | 76.44 | 100.00 | 1.977 | 1.295 |
| Denmark | 87.74 | 98.57 | 0.006 | 8.742 | 99.78 | 100.00 | 4.652 | 1.112 |
| Finland | 79.10 | 98.07 | 0.010 | 9.545 | 100.00 | 100.00 | 5.760 | 1.542 |
| France | 99.88 | 99.89 | 0.018 | 1.517 | 100.00 | 100.00 | 9.955 | 1.131 |
| Germany | 59.06 | 63.10 | 0.010 | 1.450 | 61.54 | 44.29 | 3.101 | 0.711 |
| Italy | 75.26 | 97.67 | 0.008 | 6.173 | 99.13 | 100.00 | 5.770 | 1.263 |
| Japan | 36.43 | 56.11 | 0.005 | 4.696 | 100.00 | 100.00 | 2.490 | 1.369 |
| Netherlands | 97.55 | 99.92 | 0.011 | 3.924 | 100.00 | 100.00 | 6.792 | 0.998 |
| Norway | 66.84 | 96.29 | 0.004 | 7.896 | 94.01 | 100.00 | 3.789 | 1.078 |
| Spain | 84.09 | 99.99 | 0.006 | 4.656 | 100.00 | 100.00 | 5.720 | 1.219 |
| Sweden | 90.88 | 99.16 | 0.009 | 7.251 | 100.00 | 100.00 | 7.124 | 1.387 |
| Switzerland | 91.27 | 94.82 | 0.010 | 3.979 | 100.00 | 100.00 | 5.183 | 0.847 |
| United Kingdom | 71.22 | 88.34 | 0.007 | 4.460 | 92.36 | 100.00 | 5.476 | 0.968 |
| United States | 67.80 | 82.29 | 0.006 | 1.377 | 99.81 | 99.81 | 2.488 | 0.933 |
| SOURCE: Author's calculations | ||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||
| Country | Age dependency ratio δ1 | Age dependency ratio δ2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Empirical coverage (percent) | Average width | Empirical coverage (percent) | Average width | |||||
| LC | AR(1) | LC | AR(1)/LC | LC | AR(1) | LC | AR(1)/LC | |
| Austria | 41.03 | 24.99 | 0.043 | 0.834 | 36.59 | 26.54 | 0.035 | 1.015 |
| Belgium | 54.24 | 100.00 | 0.057 | 1.088 | 35.38 | 91.71 | 0.042 | 1.302 |
| Canada | 39.44 | 100.00 | 0.024 | 1.943 | 30.45 | 100.00 | 0.020 | 2.258 |
| Denmark | 95.33 | 100.00 | 0.052 | 1.843 | 91.76 | 100.00 | 0.038 | 2.401 |
| Finland | 59.16 | 100.00 | 0.061 | 1.792 | 38.01 | 100.00 | 0.042 | 2.292 |
| France | 100.00 | 100.00 | 0.114 | 0.827 | 100.00 | 100.00 | 0.084 | 1.131 |
| Germany | 52.81 | 57.84 | 0.044 | 0.966 | 54.56 | 59.74 | 0.039 | 1.020 |
| Italy | 58.58 | 100.00 | 0.069 | 1.597 | 38.65 | 100.00 | 0.055 | 1.766 |
| Japan | 95.17 | 100.00 | 0.039 | 1.840 | 79.44 | 100.00 | 0.034 | 2.019 |
| Netherlands | 100.00 | 100.00 | 0.082 | 1.363 | 100.00 | 100.00 | 0.065 | 1.545 |
| Norway | 34.66 | 100.00 | 0.038 | 1.902 | 25.80 | 100.00 | 0.026 | 2.608 |
| Spain | 100.00 | 100.00 | 0.071 | 1.550 | 100.00 | 100.00 | 0.057 | 1.727 |
| Sweden | 100.00 | 100.00 | 0.086 | 1.916 | 99.65 | 100.00 | 0.067 | 2.191 |
| Switzerland | 95.71 | 95.87 | 0.070 | 0.935 | 88.41 | 95.87 | 0.058 | 1.051 |
| United Kingdom | 42.23 | 100.00 | 0.058 | 1.548 | 26.36 | 100.00 | 0.042 | 1.962 |
| United States | 99.81 | 99.81 | 0.040 | 0.920 | 99.62 | 98.72 | 0.036 | 0.890 |
| SOURCE: Author's calculations | ||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||
Beginning with the age profile, it is evident that over all the age groups, the first-order autoregressive approach yields interval projections in every single case that exhibit greater probability content than the Lee-Carter model, but are also much wider. In general, the LC model seems more likely to generate mortality intervals that are "too narrow" (that is., that fall below their nominal 90-percent level of coverage). Conversely, the AR(1) model tends to produce intervals that are "too wide." For instance, with the LC model, only 4 nations exhibit coverage greater than or equal to 90 percent (France, the Netherlands, Sweden, and Switzerland), while in 9 of the 16 cases empirical coverage falls below 80 percent. By contrast, with the first-order autoregressive approach, probability content is in excess of 90 percent in nine of the data sets, whereas only three countries exhibit coverage below 80 percent (Austria, Germany and Japan). On average, the interval forecasts of mortality produced by the AR(1) model are wider than those of the LC approach by a factor ranging from less than one-and-a-half times wider for the United States, to nearly 10 times wider for Finland (fourth column in Table 12).
Turning to the projections of life expectancy at birth, it is clear that both models tend to generate intervals that are "too wide." With the exceptions of Austria and Germany in the AR(1) model and Austria, Canada, and Germany in the LC approach, empirical coverage exceeds 90 percent for the remaining countries and is either equal or closer to 100 percent in most cases. Moreover, the differences in size between the interval forecasts generated by the two models are far less pronounced than for the age profile. In roughly half of the data sets, each model produces narrower intervals on average than the other. These findings highlight the type of cancellation effects that can occur when the age-specific mortality forecasts are combined to produce such a highly nonlinear aggregate measure of overall performance. Consider, for instance, the interval projections corresponding to Japan. In this case, over all age groups and forecasts horizons the 90 percent interval projections generated by the Lee-Carter model contain observed mortality only 36 percent of the time. However, when the simulated paths are used to compute e0, all 276 interval forecasts of life expectancy at birth contain the corresponding ex-post values, resulting in 100-percent probability coverage.10 The converse can also be the case. In the AR(1) approach, the interval projections of mortality for Austria over the age profile have an empirical probability content of 74 percent, while those associated with the LC model yield 66-percent coverage. Yet, for the latter model, the interval forecasts of life expectancy display 71-percent coverage, with an average width of 3.6 years over all forecast horizons. By contrast, the projections of life expectancy generated by the AR(1) model exhibit extremely poor coverage (24 percent) and are half the size of those produced by the LC approach.
For the OASDI program, a more useful performance evaluation criterion regarding the age-specific mortality forecasts generated by the models involves the forecast error associated with the age dependency ratios presented in Table 13. In this case, with the exceptions of Austria and Germany, where empirical coverage is quite poor, the first-order autoregressive approach produces interval forecasts with probability content in excess of 90 percent for both measures δ1 and δ2. On the other hand, the Lee-Carter model generates intervals that are "too narrow" for half of the data sets and "too wide" for the other half. Specifically, empirical coverage in Austria, Belgium, Canada, Finland, Germany, Italy, Norway and the United Kingdom falls below 60 percent. Not surprisingly, the AR(1) model generates wider interval projections than the LC model in 11 cases for δ1, and 15 cases for δ2.
Finally, Table 14 shows the performance of the interval projections generated by the models over the three broad age categories previously defined. In general, the Lee-Carter model tends to produce interval forecasts of mortality that exceed their hypothetical probability content at the youngest ages, but seriously underestimate it for the older age groups. For instance, in the 0–19 age category there are 12 cases with coverage in excess of 90 percent and only 3 countries with coverage below 80 percent (Germany, Japan and the United States). By contrast, for the retirement ages (65–95 or older), coverage stays above 90 percent in 2 countries (France and the Netherlands), while it falls below 80 percent in the remaining 14 countries. On the other hand, for all three age categories (0–19, 20–64, and 65–95 or older), the first-order autoregressive approach generates interval forecasts with over 90-percent probability content in the majority of instances. Moreover, in every single case the AR(1) interval projections are narrower than those of the LC model for the youngest ages, but much wider for the 65–95 or older age class.
| Country | Ages 0–19 | Ages 20–64 | Aged 65–95 or oder | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Empirical coverage (percent) | Average width | Empirical coverage (percent) | Average width | Empirical coverage (percent) | Average width | ||||
| LC | AR(1) | AR(1)/LC | LC | AR(1) | AR(1)/LC | LC | AR(1) | AR(1)/LC | |
| Austria | 85.07 | 97.20 | 0.452 | 81.22 | 76.91 | 0.963 | 32.85 | 54.96 | 4.086 |
| Belgium | 99.62 | 99.12 | 0.506 | 92.18 | 91.82 | 1.033 | 56.23 | 78.30 | 3.142 |
| Canada | 97.35 | 97.63 | 0.804 | 55.78 | 68.16 | 1.699 | 49.42 | 88.67 | 5.217 |
| Denmark | 98.38 | 98.28 | 0.762 | 94.61 | 97.80 | 1.215 | 71.33 | 99.78 | 10.820 |
| Finland | 99.69 | 99.26 | 0.559 | 86.45 | 98.24 | 1.926 | 54.94 | 96.98 | 11.065 |
| France | 100.00 | 100.00 | 0.571 | 100.00 | 100.00 | 1.638 | 99.64 | 99.67 | 1.558 |
| Germany | 77.00 | 66.16 | 0.377 | 48.93 | 54.09 | 0.976 | 59.26 | 72.47 | 1.518 |
| Italy | 99.96 | 90.21 | 0.584 | 88.58 | 100.00 | 1.551 | 40.49 | 100.00 | 7.279 |
| Japan | 36.74 | 38.22 | 0.538 | 34.93 | 35.72 | 0.858 | 38.15 | 95.12 | 5.093 |
| Netherlands | 99.86 | 99.67 | 0.558 | 100.00 | 100.00 | 1.097 | 92.75 | 100.00 | 4.475 |
| Norway | 93.22 | 91.51 | 0.732 | 85.65 | 96.45 | 1.298 | 23.80 | 99.51 | 10.172 |
| Spain | 99.96 | 99.96 | 0.713 | 93.41 | 100.00 | 1.434 | 60.78 | 100.00 | 5.615 |
| Sweden | 99.33 | 96.47 | 0.513 | 99.98 | 100.00 | 1.560 | 73.14 | 100.00 | 8.693 |
| Switzerland | 97.16 | 98.09 | 0.530 | 96.77 | 96.65 | 1.025 | 79.99 | 90.14 | 4.363 |
| United Kingdom | 100.00 | 92.49 | 0.479 | 85.39 | 85.31 | 1.119 | 32.44 | 89.26 | 5.503 |
| United States | 72.73 | 86.30 | 0.700 | 59.03 | 79.48 | 1.226 | 75.57 | 83.04 | 1.414 |
| SOURCE: Author's calculations | |||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | |||||||||
Performance by Forecast Horizon
Table 15 displays the empirical probability content and ratio of average width corresponding to the 90-percent interval projections of the models over the age profile and various forecast horizons (1–5, 6–10, 11–15 and 16 or more years ahead). Tables 16 through 18 present similar quantities for the interval projections of life expectancy at birth e0 and the two age dependency measures δ1 and δ2. Although not always the case, coverage over the age profile tends to decrease with the length of the forecast horizon. For the 1–5 year period, the LC and AR(1) models generate interval forecasts with over 80-percent coverage in 10 and all 16 countries, respectively. Out of these countries, coverage exceeds the hypothetical 90-percent level in 6 cases for the LC model and 12 cases for AR(1) approach. On the other hand, for the most distant forecast period (the 16 or more year horizon), probability content lies above 80 percent in 6 countries for the LC model and 10 countries for AR(1) approach. Even at this forecast length, coverage exceeds 90 percent in half of all cases for the latter model. In terms of the size of the generated intervals, the LC model generates narrower projections over the age profile than the AR(1) model across all forecast horizons. As previously mentioned, this is because interval projections for the oldest age groups in the first-order autoregressive approach are much wider.
| Country | Empirical coverage LC (percent) | Empirical coverage AR(1) (percent) | Average width AR(1)/LC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 74.40 | 73.15 | 68.16 | 54.97 | 86.38 | 81.83 | 73.84 | 62.69 | 3.391 | 3.226 | 3.425 | 3.825 |
| Belgium | 91.62 | 86.60 | 78.58 | 75.16 | 97.09 | 94.05 | 86.25 | 82.65 | 2.933 | 2.749 | 2.757 | 2.877 |
| Canada | 68.60 | 65.22 | 62.07 | 60.30 | 92.80 | 85.96 | 78.96 | 74.72 | 4.635 | 4.398 | 4.528 | 4.829 |
| Denmark | 83.44 | 87.29 | 89.52 | 89.24 | 97.44 | 97.61 | 98.55 | 99.63 | 8.199 | 7.950 | 8.338 | 9.301 |
| Finland | 90.09 | 87.30 | 77.43 | 68.14 | 99.05 | 99.09 | 97.97 | 96.88 | 7.861 | 8.143 | 9.007 | 10.929 |
| France | 99.45 | 100.00 | 100.00 | 100.00 | 99.86 | 100.00 | 99.63 | 100.00 | 1.634 | 1.530 | 1.511 | 1.489 |
| Germany | 72.32 | 67.19 | 63.57 | 42.87 | 80.82 | 73.46 | 69.18 | 41.74 | 1.602 | 1.454 | 1.419 | 1.430 |
| Italy | 88.85 | 80.80 | 73.01 | 64.71 | 99.65 | 99.55 | 97.45 | 95.39 | 5.788 | 5.807 | 6.046 | 6.474 |
| Japan | 75.53 | 49.42 | 25.26 | 10.87 | 83.94 | 64.89 | 48.02 | 38.29 | 4.086 | 4.158 | 4.545 | 5.225 |
| Netherlands | 95.96 | 98.19 | 98.30 | 97.67 | 99.63 | 100.00 | 100.00 | 100.00 | 3.990 | 3.773 | 3.826 | 4.009 |
| Norway | 72.26 | 70.65 | 66.57 | 61.23 | 94.95 | 94.11 | 94.54 | 99.59 | 7.717 | 7.395 | 7.694 | 8.265 |
| Spain | 87.63 | 83.28 | 81.56 | 83.99 | 99.96 | 100.00 | 100.00 | 100.00 | 4.557 | 4.421 | 4.523 | 4.829 |
| Sweden | 92.63 | 94.20 | 93.31 | 86.71 | 99.34 | 98.58 | 98.62 | 99.68 | 7.009 | 6.892 | 7.086 | 7.497 |
| Switzerland | 90.17 | 93.94 | 95.03 | 88.61 | 97.52 | 98.99 | 97.68 | 89.95 | 4.019 | 3.806 | 3.884 | 4.064 |
| United Kingdom | 87.02 | 80.69 | 69.02 | 58.39 | 98.65 | 95.06 | 89.78 | 78.07 | 4.632 | 4.349 | 4.366 | 4.503 |
| United States | 71.20 | 69.71 | 68.12 | 64.29 | 86.42 | 85.39 | 87.48 | 74.52 | 1.623 | 1.463 | 1.384 | 1.283 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||||||
Table 16 shows the empirical content of the interval projections of life expectancy at birth. Clearly, with the exceptions of Austria and Germany, where coverage deteriorates with the length of the forecast horizon, both models generate intervals that are "too wide." For most of the data sets there is 100 percent coverage at every forecast horizon. The forecast intervals of e0 produced by the LC model are narrower than those of the AR(1) approach in 11 cases for the 1–5 year period, and 10 cases for the remaining forecast horizons.
| Country | Empirical coverage LC (percent) | Empirical coverage AR(1) (percent) | Average width AR(1)/LC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 100.00 | 100.00 | 95.78 | 21.18 | 79.31 | 30.57 | 3.21 | 0.00 | 0.577 | 0.546 | 0.538 | 0.538 |
| Belgium | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 0.868 | 0.833 | 0.828 | 0.839 |
| Canada | 100.00 | 100.00 | 94.29 | 35.83 | 100.00 | 100.00 | 100.00 | 100.00 | 1.258 | 1.240 | 1.282 | 1.335 |
| Denmark | 100.00 | 98.89 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.181 | 1.093 | 1.094 | 1.112 |
| Finland | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.425 | 1.420 | 1.480 | 1.659 |
| France | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.132 | 1.224 | 1.184 | 1.066 |
| Germany | 98.95 | 92.27 | 84.37 | 4.69 | 95.84 | 66.10 | 41.81 | 0.00 | 0.725 | 0.704 | 0.706 | 0.713 |
| Italy | 100.00 | 100.00 | 100.00 | 97.50 | 100.00 | 100.00 | 100.00 | 100.00 | 1.355 | 1.290 | 1.256 | 1.233 |
| Japan | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.161 | 1.220 | 1.342 | 1.526 |
| Netherlands | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.059 | 0.995 | 0.991 | 0.988 |
| Norway | 99.00 | 89.69 | 83.73 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.113 | 1.064 | 1.061 | 1.083 |
| Spain | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.257 | 1.208 | 1.204 | 1.221 |
| Sweden | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.465 | 1.402 | 1.385 | 1.368 |
| Switzerland | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 0.902 | 0.852 | 0.842 | 0.836 |
| United Kingdom | 100.00 | 100.00 | 100.00 | 79.63 | 100.00 | 100.00 | 100.00 | 100.00 | 1.041 | 0.980 | 0.966 | 0.949 |
| United States | 99.13 | 100.00 | 100.00 | 100.00 | 99.13 | 100.00 | 100.00 | 100.00 | 0.882 | 0.908 | 0.925 | 0.959 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||||||
Finally, Tables 17 and 18 present the empirical probability coverage of the interval forecasts for the age-dependency ratios δ1 and δ2. Clearly, for the Lee-Carter model, performance tends to deteriorate dramatically with the distance of the forecast horizon. By contrast, with the exceptions of Austria and Germany, the AR(1) approach yields interval projections with 100-percent probability content in the large majority of cases across all forecast periods. For instance, over the 1–5 year horizon, coverage in the LC model exceeds 80 percent in 15 cases for δ1, and in 13 cases for δ2. On the other hand, over the longest forecast period (16 or more years ahead), these quantities drop down to 8 and 6 cases, respectively. In fact, for this same period, probability content in the LC model is actually 0 percent in five and eight nations for the δ1 and δ2 ratios, respectively. Conversely, over the 16 or more years horizon, the AR(1) approach yields coverage in excess of 90 percent in 13 and 12 cases. Generally, the interval forecasts corresponding to the first-order autoregressive approach are wider on average than those of the LC model.
| Country | Empirical coverage LC (percent) | Empirical coverage AR(1) (percent) | Average width AR(1)/LC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 92.16 | 66.38 | 30.19 | 0.00 | 78.27 | 35.15 | 1.54 | 0.00 | 0.903 | 0.830 | 0.818 | 0.828 |
| Belgium | 91.20 | 80.63 | 58.63 | 11.91 | 100.00 | 100.00 | 100.00 | 100.00 | 1.125 | 1.068 | 1.071 | 1.096 |
| Canada | 73.99 | 69.83 | 37.63 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.938 | 1.868 | 1.909 | 1.993 |
| Denmark | 92.94 | 87.91 | 95.80 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.979 | 1.820 | 1.816 | 1.835 |
| Finland | 99.13 | 90.72 | 66.10 | 10.12 | 100.00 | 100.00 | 100.00 | 100.00 | 1.721 | 1.662 | 1.725 | 1.902 |
| France | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 0.863 | 0.822 | 0.819 | 0.825 |
| Germany | 98.95 | 88.43 | 55.56 | 0.00 | 98.95 | 88.43 | 70.84 | 4.91 | 1.007 | 0.957 | 0.953 | 0.966 |
| Italy | 98.13 | 93.52 | 63.08 | 9.20 | 100.00 | 100.00 | 100.00 | 100.00 | 1.697 | 1.619 | 1.588 | 1.570 |
| Japan | 95.61 | 98.82 | 100.00 | 89.58 | 100.00 | 100.00 | 100.00 | 100.00 | 1.638 | 1.669 | 1.798 | 2.002 |
| Netherlands | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.460 | 1.356 | 1.350 | 1.351 |
| Norway | 80.67 | 49.54 | 29.24 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.982 | 1.888 | 1.883 | 1.899 |
| Spain | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.592 | 1.518 | 1.524 | 1.565 |
| Sweden | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.006 | 1.929 | 1.914 | 1.894 |
| Switzerland | 99.20 | 100.00 | 100.00 | 89.67 | 100.00 | 100.00 | 100.00 | 89.67 | 1.003 | 0.928 | 0.923 | 0.929 |
| United Kingdom | 91.74 | 77.30 | 33.69 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.709 | 1.572 | 1.542 | 1.509 |
| United States | 99.13 | 100.00 | 100.00 | 100.00 | 99.13 | 100.00 | 100.00 | 100.00 | 0.949 | 0.919 | 0.915 | 0.917 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||||||
| Country | Empirical coverage LC (percent) | Empirical coverage AR(1)(percent) | Average width AR(1)/LC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | 1–5 | 6–10 | 11–15 | 16 or more | |
| Austria | 87.24 | 61.34 | 19.72 | 0.00 | 82.96 | 37.58 | 1.54 | 0.00 | 1.077 | 0.992 | 0.987 | 1.024 |
| Belgium | 85.38 | 53.00 | 24.37 | 0.00 | 95.12 | 92.84 | 94.64 | 87.05 | 1.348 | 1.274 | 1.278 | 1.315 |
| Canada | 68.42 | 54.41 | 17.25 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.276 | 2.175 | 2.208 | 2.314 |
| Denmark | 87.62 | 84.48 | 89.22 | 98.75 | 100.00 | 100.00 | 100.00 | 100.00 | 2.591 | 2.381 | 2.369 | 2.384 |
| Finland | 86.78 | 61.57 | 26.50 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.148 | 2.097 | 2.198 | 2.460 |
| France | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 0.973 | 1.082 | 1.149 | 1.180 |
| Germany | 98.95 | 91.10 | 60.91 | 0.00 | 98.95 | 93.38 | 74.60 | 4.91 | 1.069 | 1.012 | 1.007 | 1.019 |
| Italy | 94.13 | 67.32 | 16.36 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.891 | 1.798 | 1.754 | 1.731 |
| Japan | 89.73 | 95.27 | 96.46 | 52.49 | 100.00 | 100.00 | 100.00 | 100.00 | 1.828 | 1.843 | 1.971 | 2.178 |
| Netherlands | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.665 | 1.538 | 1.529 | 1.529 |
| Norway | 61.45 | 42.13 | 15.12 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.760 | 2.613 | 2.593 | 2.578 |
| Spain | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 1.813 | 1.713 | 1.702 | 1.725 |
| Sweden | 98.33 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.278 | 2.195 | 2.187 | 2.173 |
| Switzerland | 99.20 | 100.00 | 98.33 | 72.25 | 100.00 | 100.00 | 100.00 | 89.67 | 1.136 | 1.050 | 1.040 | 1.039 |
| United Kingdom | 79.42 | 41.04 | 6.06 | 0.00 | 100.00 | 100.00 | 100.00 | 100.00 | 2.171 | 1.985 | 1.944 | 1.919 |
| United States | 98.26 | 100.00 | 100.00 | 100.00 | 99.13 | 100.00 | 100.00 | 96.88 | 0.947 | 0.899 | 0.887 | 0.876 |
| SOURCE: Author's calculations | ||||||||||||
| NOTES: LC = Lee-Carter Model; AR(1) = Lag 1 autoregression. | ||||||||||||
Conclusion
This paper evaluates the out-of-sample forecast performance of two stochastic models used to forecast age-specific mortality rates: (1) a variant of the Lee-Carter (LC) model that accommodates bias correction for the jump off year; and (2) a set of univariate first-order autoregressions AR(1) with a common residual covariance matrix. To this aim, mortality data from 16 industrialized nations, each comprising 21 different age groups is used to compare observed ex-post mortality rates to the forecasts produced by the models. To assess overall model performance, several functions of the individual age-specific mortality rates are entertained, including forecast error over the entire age profile, life expectancy at birth e0, and two alternative measures of the age-dependency ratio. The first measure (denoted δ1) involves the ratio of population ages 65–95 or older to those ages 20–64. The second criterion (δ2) entails a broader measure of dependency that includes both the youngest and oldest age groups (the ratio of population ages 0–19 and ages 65–95 or older to those aged 20–64).
With few exceptions, it is generally found that the differences in RMSE associated with the median projections of the models are not substantial. In most cases, the median forecasts of both models tend to moderately overpredict actual mortality over the age profile. This is particularly the case for the retirement ages (65–95 or older), where a high proportion of the forecasts corresponding to the oldest age groups overestimate mortality. Conversely, the large majority of the median forecasts of e0, δ1 and δ2 underestimate their observed values, with the proportion of forecasts involving underestimation increasing with the length of the forecast horizon.
The retirement ages account for the overwhelming majority of total forecast error over the age profile. For the youngest age category (ages 0–19), the first order autoregressive approach outperforms the LC model in 11 of the 16 countries considered. However, over all ages and forecast horizons each model displays lower RMSE than the other in half of all cases. The same is true for the median projections of e0 and δ1, where over all forecast periods, each model outperforms the other in roughly half of the data sets entertained. On the other hand, the median projections of δ2 corresponding to the AR(1) model exhibit lower forecast error than those of the LC method in 11 cases. In the very short-run (1–5 year horizons), the LC model outranks the AR(1) approach in 13 countries for the median forecasts of e0, and 10 countries for the median projections of δ1 and δ2.
While differences in the performance of the point projections of both models tend to be fairly small, much more variation is found in the performance of the generated 90-percent confidence interval forecasts. The AR(1) approach typically produces interval projections of mortality across all ages that are close to and often exceed their hypothetical 90-percent probability content. The LC model also generates interval forecasts with adequate empirical coverage for the youngest age groups (ages 0–19), but seriously underestimates the 90-percent level of coverage for the retirement ages (65–95 or older). Not surprisingly, the AR(1) approach produces much wider intervals on average than the LC model for the oldest age category, although it also yields narrower projections for the youngest ages. Hence, over the entire age profile, the LC model is more likely to generate interval projections that are "too narrow," whereas the AR(1) method tends to produce interval forecasts that are "too wide."
For life expectancy at birth e0, both models clearly generate interval forecasts that are "too wide" (that is, with coverage in excess of 90 percent). In fact, for the large majority of countries the empirical probability content of the projections of e0 is 100 percent, even over the longest forecast horizons (16 or more years ahead). With a couple of exceptions, the AR(1) approach also generates interval forecasts of the dependency ratios δ1 and δ2 with 100-percent empirical coverage. In this case, however, the projections of the LC model deteriorate quickly with the length of the forecast period, so that at the 16 or more years horizon, coverage is adequate in about half of the data, but extremely poor for the other half. Indeed, over this same forecast period the LC interval projections of δ2 in 8 of the 16 countries never contain their corresponding ex-post values (that is, there is 0 percent probability content).
From the perspective of a pay-as-you-go public retirement program, the age-dependency ratios seem to be more relevant performance evaluation criteria than either the projections of life expectancy at birth or the age profile. In light of the evidence suggesting the tendency of the Lee-Carter model to underestimate forecast uncertainty for these ratios, a conservative approach to modeling mortality appears to favor the first-order autoregressive model.
Notes
1 Alternatively, the first p principal components can be defined as the eigenvectors corresponding to the largest p eigenvalues of the product
2 See for instance Girosi and King (2004; Chapter 2).
3 Notice that there are alternative ways to implement bias correction in the Lee-Carter model. For instance, Lee and Carter (1992) suggest setting the value of αa to the most recent rates prior to performing SVD, while ignoring the normalization constraint on kt. By contrast, Lee (2000) favors estimating the model as originally proposed, prior to changing αa. This paper follows the latter approach.
4 The Congressional Budget Office's stochastic model of Social Security's long-term trust fund finances uses a similar approach (CBO; 2000).
5 The HMD is a collaborative project sponsored by the University of California at Berkeley and the Max Planck Institute for Demographic Research. The data, as well as both general and country specific documentation can be accessed via www.mortality.org or www.humanmortality.de.
6 The mortality rates corresponding to Germany were obtained by pooling the death counts and risk-to-exposure estimates listed separately for East and West Germany in the HMD. The U.K. data comprises England and Wales.
7 Notice that Lee and Miller (2001) employ a different variation in the second stage estimation of kt, matching life expectancy for that year instead of total number of deaths.
8 For single-year ages except age 0, is usually set to one-half, under the assumption that deaths occur uniformly. In addition, notice that for period life table calculations, the mortality rates are transformed into probabilities of death using standard procedures.
9 For comparison, the corresponding values reported in Table V.A2 of the 2005 Trustees Report, based on the total Social Security area population at mid-year in 2000 are respectively and
10 See the last column in Table 1.
References
Bell, W. 1997. Comparing and assessing time series methods for forecasting age-specific fertility and mortality rates. Journal of Official Statistics 13(3): 279–303.
Bell, W., and B. Monsell. 1991. Using principal components in time series modeling and forecasting of age-specific mortality rates. Paper presented at the 1991 Annual Meetings of the Population Association of America, Washington, DC.
Board of Trustees of the Federal Old-Age and Survivors Insurance and Disability Insurance Trust Funds. 2005. 2005 Annual Report. Washington, DC: U.S. Government Printing Office.
Congressional Budget Office. 2001. Uncertainty in Social Security's long-term finances: A stochastic analysis. Washington, DC: U.S. Government Printing Office.
Denton, F. T., C. H. Feaver, and B. G. Spencer. 2005. Time series analysis and stochastic forecasting: An econometric study of mortality and life expectancy. Journal of Population Economics 18: 203–227.
Girosi, F., and G. King. 2004. Demographic Forecasting. Unpublished book manuscript.
Lee, R. D. 2000. The Lee-Carter method for forecasting mortality, with various extensions and applications. North American Actuarial Journal 4(1): 80–91.
Lee, R. D., and L. R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–671.
Lee, R. D., and T. Miller. 2001. Evaluating the performance of the Lee-Carter method for forecasting mortality. Demography 38(4): 537–549.
Wilmoth, J. 1993. Computational methods for fitting and extrapolating the Lee-Carter model of mortality change. Technical Report, Department of Demography, University of California, Berkeley.
———. Methods protocol for the human mortality database. Technical Report. Available at www.mortality.org.