The Effects of Wage Indexing on Social Security Disability Benefits
Social Security Bulletin, Vol. 68, No. 3, 2008
Researchers David Autor and Mark Duggan have hypothesized that the Social Security benefit formula using the average wage index, coupled with a widening distribution of income, has created an implicit rise in replacement rates for low-earner disability beneficiaries. This research attempts to confirm and quantify the replacement rate creep identified by Autor and Duggan using actual earnings histories of disability-insured workers over the period 1979–2004. The research finds that disability replacement rates are rising for many insured workers, although the effect may be somewhat smaller than that suggested by Autor and Duggan.
The author is with the Office of Research, Evaluation and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: The author acknowledges the contributions of Jae Song, who provided the CWHS data used in this study; and of Mark Duggan and Paul Van de Water, who offered their insight with respect to the conduct of this study. Acknowledgments are also due to Michael Compson, Eli Donkar, Jeffrey Hemmeter, Russ Hudson, Mike Leonesio, and Joyce Manchester, who offered comments on an earlier draft.
The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Summary and Introduction
Economists David Autor and Mark Duggan have hypothesized that the Social Security Administration's (SSA's) use of the average wage index (AWI) in its benefit formula, coupled with a widening distribution of income, has created an implicit rise in replacement rates for low-earner disability beneficiaries. They point out that the actual disability benefit received depends implicitly on the individual's earnings growth relative to the growth of earnings for all workers over the benefit calculation period.
This article examines the effect that indexing using the AWI has had on Social Security benefits. To the extent possible, the article tests the Autor and Duggan hypothesis and attempts to quantify the earnings history and bracket effects using actual earnings histories of disability-insured workers. Whereas Autor and Duggan used earnings at certain percentiles of the earnings distribution to demonstrate the potential effect, this article uses actual earnings histories of disability-insured workers to estimate the benefit and replacement rates that each worker would have received if he or she became disabled over the period 1979 to 2004 and to determine if these are, in fact, rising.
This article demonstrates that the distribution of Social Security–reported annual earnings is widening, with the highest earners receiving larger increases. Hence, the AWI may overstate growth for lower earners. Using the Continuous Work History Sample, the article shows that over time replacement rates for many workers have been increasing relative to recent earnings and, as a result, may be increasing incentives to seek disability benefits.
In an alternate approach, a different, more representative index of earnings growth for the majority of workers is used to create a counterfactual, permitting the decomposition of replacement rate changes into the "earnings history" and "bracket" effects identified by Autor and Duggan. Results suggest that both effects have led to higher replacement rates, but the bracket effect appears to contribute most to the trend. Direct comparisons are made between the results from this article, using actual earnings histories, and those obtained in Autor and Duggan's 2006 article.
Finally, this article analyzes the potential impact of using alternative methods of indexing on benefits, replacement rates, and program solvency. For example, an index based on median earnings growth could help solvency not only for the disability program, but for the retirement program as well. The analysis suggests that progressive indexing could exacerbate problems with incentives to seek benefits and result in a less efficient solution to long-term solvency issues.
Tables presenting detailed data underlying the charts in this article are available as Appendices B and C at http://www.socialsecurity.gov/policy/docs/ssb/v68n3/v68n3p1_app.html.
Background
In the early years of Social Security, the benefit calculation was static, with Congress legislatively granting ad hoc increases in benefits to account for increases in the cost of living or for other reasons. In 1972, Congress passed legislation that provided for automatic annual cost-of-living adjustments (COLAs) to benefits based on the Consumer Price Index (CPI). The first annual COLA for Social Security benefits occurred in June 1975. Adjustments were made to the benefit formula by increasing the percentage of the average monthly wage (AMW) applicable to the primary insurance amount (PIA) at each bend point in the formula. As the taxable maximum increased each year, an additional bend point was also added to the formula.
Before long it became apparent that this method of adjustment resulted not only in higher benefits, but also in higher real benefits for successive cohorts. Inflation increased not only the cost of living and hence the CPI, but generally resulted in higher earnings as well. Higher AMWs and the CPI-adjusted benefit formula resulted in overcompensation for the effects of inflation, increasing real benefits and program costs. Congress debated solutions to the unintended problem and, with the 1977 Amendments to the Social Security Act (P.L. 95-216), legislated a new benefit formula that "decoupled" the COLA from the increase in the wage base.1 After much debate, Congress decided to adjust the benefit for current beneficiaries using the CPI, but to use an average wage index to adjust the earnings history used in computing the initial benefit (PIA).2 Using the CPI to adjust earnings, it was argued, would lead to declining replacement rates for successive cohorts of beneficiaries.3 Adjusting earnings using a wage index would stabilize replacement rates for successive cohorts. Considered somewhat differently, indexing earnings for price changes would provide benefits based on the worker's share of prior real production, while indexing earnings for wage changes provides benefits based on the individual's share of current production. In essence, Congress chose to offer benefits based on the standard of living at the time of entitlement, rather than a weighted average of the standard of living over the worker's working lifetime. At the time, some argued that using wage-indexing in the calculation of benefits would not be sustainable.4
The Decoupled Benefit Calculation
The 1977 amendments were passed to address, among other things, the inadvertent increase in benefits caused by the automatic indexing method enacted in 1972 and begun in June 1975. The 1977 amendments provided for the indexation of the worker's earnings history to create an average indexed monthly earnings (AIME) measure to replace the AMW.5 The individual's earnings history is indexed to wage levels in the national economy 2 years prior to the year of benefit eligibility6 using a measure of average wages for all workers.7 The 1977 amendments also created a new benefit formula for calculating the PIA that uses fixed replacement rates (90 percent, 32 percent, and 15 percent) and variable formula bend points that are annually adjusted using a wage index. The formula for computing the maximum family benefit amount (MFBA) was also changed by the 1977 amendments and uses fixed replacement rates and a variable bend point formula that is wage indexed. The national average wage is used to make the wage-indexed adjustments to the individual's earnings history, the bend points in the PIA and MFBA formulas, and the taxable maximum of annual earnings. The individual's benefit is calculated at the time of eligibility,8 and the beneficiary receives a COLA in January of each year of entitlement based on changes in the CPI.
The PIA and MFBA benefit formulas from 1979 and 2007 illustrate how wage indexing changes the formula over time:
PIA formula
1979: 90 percent of the first $180 of AIME + 32 percent of the next $905 of AIME + 15 percent of AIME over $1,085
2007: 90 percent of the first $680 of AIME + 32 percent of the next $4,100 of AIME + 15 percent of AIME over $4,780
MFBA formula9
1979: 150 percent of the first $230 of PIA + 272 percent of the next $102 of PIA + 134 percent of the next $101 of PIA + 175 percent of PIA over $433
2007: 150 percent of the first $869 of PIA + 272 percent of the next $386 of PIA + 134 percent of the next $381 of PIA + 175 percent of PIA over $1,636
Over the years larger portions of earnings (and benefits in the MFBA) are subject to the higher replacement rates. However, the indexation of the earnings history, coupled with the changes in the formulas, is intended to result in a constant replacement rate for successive cohorts of entitlements over time, as measured against near-current wage levels.10 This would be the case if earnings grew at the same rate for all individuals, but, as discussed below, it may not be the case if there are changes in the distribution of earnings.
The Autor/Duggan Hypothesis
David Autor and Mark Duggan (2003, 2006) have hypothesized that the benefit formula using the AWI, coupled with a widening distribution of income, has created an implicit rise in replacement rates for low-earner disability beneficiaries. They point out that the actual disability benefit received depends implicitly on the individual's earnings growth relative to the growth of earnings for all workers over the benefit calculation period. Autor and Duggan's work pertains specifically to disabled workers, but any impact of wage indexing on benefits also affects the benefit calculation for other beneficiaries, including retired workers.11 In their 2006 article, Autor and Duggan demonstrate the implicit increase in benefits graphically:
Illustration of the impact of earnings inequality and indexation on disability insurance benefits in 1980 and 2000
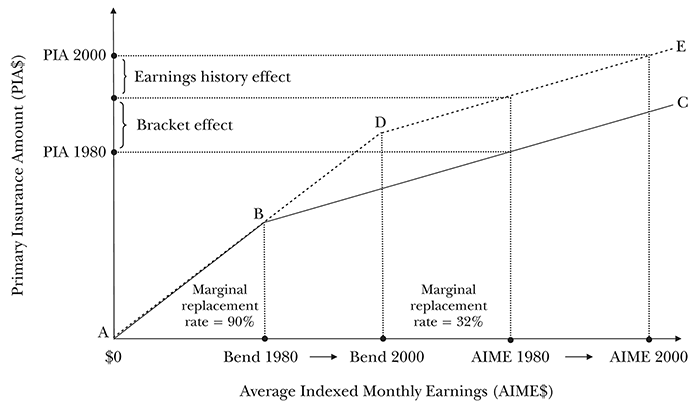
Text description for Figure 1.
Illustration of the impact of earnings inequality and indexation on disability insurance benefits in 1980 and 2000
This is an illustrative line chart. The vertical axis is labeled primary insurance amount (PIA) and the horizontal axis is labeled average indexed monthly earnings (AIME). The bottom of each scale is marked zero, but no other specific dollar values are given on either axis.
A point on the vertical axis is labeled PIA 1980; above it, another is labeled PIA 2000. Between the two is a third point, which is unlabeled. However, the gap between PIA 1980 and the third point is labeled "bracket effect," and the gap between the third point and PIA 2000 is labeled "earnings history effect."
From left to right, points on the horizontal axis are labeled "Bend 1980," "Bend 2000," "AIME 1980," and "AIME 2000."
Five points are shown in the chart. Point A is the zero-zero coordinate. Point B appears directly above Bend 1980, such that the straight line AB ascends at approximately 45 degrees. Point C appears to the extreme right of the chart at a level slightly lower than the unlabeled point on the vertical axis. The straight line BC ascends at approximately 30 degrees. Point D appears directly above Bend 2000, at a level near the midpoint of the bracket effect. The line BD continues in the trajectory of line AB, such that ABD is a straight line. Point E appears to the extreme right of the chart at a level slightly above PIA 2000. The line DE is above and parallel to line BC.
The chart also notes that PIA marginal replacement rates are 90 percent of the amount under the bend point and 32 percent of the amount over the bend point.
Autor and Duggan (2006, 71–96) explain their graph as follows:
Although DI benefits awarded are nominally only a function of a worker's prior earnings, award amounts are calculated using a wage index equal to mean wage growth economy-wide. Consequently, an individual's benefit also depends implicitly upon the individual's earnings growth relative to the growth of earnings for all workers during that worker's years of employment.
Figure [1] illustrates how this indexation scheme interacts with earnings inequality to raise the replacement rate of low-earnings workers. Line segment A-B-C depicts the benefits schedule of a worker awarded Disability Insurance benefits in 1980 whose wage growth prior to receiving DI exactly paced mean earnings in the economy. The worker's calculated average indexed monthly earnings amount (AIME) is identical to her 1980 wage. Because the benefits formula replaces between 15 and 90 percent of the marginal dollar (depending on the claimant's AIME), her monthly payment Primary Insurance Amount (PIA) falls somewhat below her 1980 wage.
Next, consider a worker, represented by line segment A-B-D-E, who is awarded Disability Insurance benefits in 2000. This worker's nominal wage history in 2000 is identical to that of the beneficiary in 1980 but, in contrast to the 1980 beneficiary, his wage growth during his career lagged contemporaneous annual average wage growth economy-wide. This worker will receive a higher real Primary Insurance Amount than the worker entering Disability Insurance in 1980. Why? The indexation of the earnings "brackets"—that is, the ranges over which income is replaced at the 90, 32 or 15 percent rates—moves these brackets upward, causing a larger share of the worker's income to be replaced at the 90 or 32 percent rates than would have been the case in 1980. We label this as the "bracket effect" in Figure [1]. Indexation also raises this worker's DI benefit through a second channel. Because the more recent worker's entire earnings history is inflated by historical mean wage growth, his average indexed monthly earnings amount will actually exceed current earnings (recall that his wage growth has lagged the economy-wide average). We label this as the "earnings history effect" in Figure [1]. Jointly, these two forces—indexation of the earnings brackets and indexation of past earnings—have substantially raised the income replacement rate of low-earnings DI beneficiaries since 1979, when earnings inequality began growing rapidly.
In essence, Autor and Duggan suggest that, if earnings rise more slowly for low earners than high earners, over time the AWI will overstate the actual wage growth of low earners, raising the value of their earnings in the calculation ("earnings history effect") and increasing the amount of predisability earnings (or lifetime earnings in the case of retirees) subject to the high replacement rate of the first bend point ("bracket effect"). The combined effect would, over time, increase implicit replacement rates and provide more incentives for low earners to seek disability benefits.12 If the hypothesized effect is actually occurring, the higher benefits and increased incentives to leave the labor force to receive those benefits combine to raise program costs and contribute to long-term solvency problems.
The impact of wage indexing on implicit replacement rates may in fact be more complex than that hypothesized by Autor and Duggan. The AWI measure is based only on the wages of persons who have wages during a given year. As employment and labor force participation patterns change, the AWI will be affected. For example, as economic conditions deteriorate, the number of individuals who are unemployed or leave the labor force for an entire year will increase and, since these individuals are not included in the calculation of average wages, that measure will tend to show higher average wages than would be the case if the nonearners were included. Hence, average wage figures based only on those who actually have earned income in a year will influence the AWI, most likely overstating wage growth during times of poor economic conditions. Similarly, during good economic times when marginal workers tend to enter the labor force, their low wages may offset some of the wage gains of the workers with greater labor force attachment, tending to hold down the AWI.13
Actual Trends in Replacement Rates for Newly Entitled Disability Beneficiaries
Recent research has examined the replacement rates among newly entitled disabled-worker beneficiaries for the period 1979 to 2000 (Muller and Lee 2004). The research shows that replacement rates based on individuals' actual PIA and their lifetime earnings (Chart 1, using the AIME as the denominator to calculate replacement rates) show a decline until about 1983, likely because persons with disability onset before 1979 were eligible for benefits based on the old, undecoupled benefit formula. Median and quartile replacement rates have been relatively constant since 1983, as was intended by the legislation that established the new (decoupled) indexing formula. Median and 75th percentile replacement rates based on lifetime earnings actually show very slight declines for those entering the rolls after 1990, but certainly not an increase in replacement rates.
Median and quartile replacement rates for newly entitled disabled-worker beneficiaries based on lifetime indexed earnings (AIME), 1979–2000
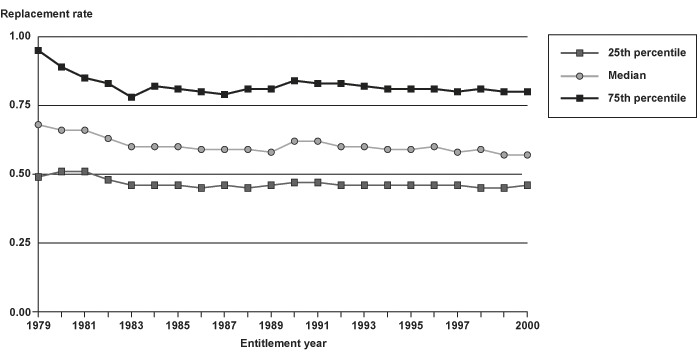
| Entitlement year | 25th percentile |
Median | 75th percentile |
|---|---|---|---|
| 1979 | 0.49 | 0.68 | 0.95 |
| 1980 | 0.51 | 0.66 | 0.89 |
| 1981 | 0.51 | 0.66 | 0.85 |
| 1982 | 0.48 | 0.63 | 0.83 |
| 1983 | 0.46 | 0.60 | 0.78 |
| 1984 | 0.46 | 0.60 | 0.82 |
| 1985 | 0.46 | 0.60 | 0.81 |
| 1986 | 0.45 | 0.59 | 0.80 |
| 1987 | 0.46 | 0.59 | 0.79 |
| 1988 | 0.45 | 0.59 | 0.81 |
| 1989 | 0.46 | 0.58 | 0.81 |
| 1990 | 0.47 | 0.62 | 0.84 |
| 1991 | 0.47 | 0.62 | 0.83 |
| 1992 | 0.46 | 0.60 | 0.83 |
| 1993 | 0.46 | 0.60 | 0.82 |
| 1994 | 0.46 | 0.59 | 0.81 |
| 1995 | 0.46 | 0.59 | 0.81 |
| 1996 | 0.46 | 0.60 | 0.81 |
| 1997 | 0.46 | 0.58 | 0.80 |
| 1998 | 0.45 | 0.59 | 0.81 |
| 1999 | 0.45 | 0.57 | 0.80 |
| 2000 | 0.46 | 0.57 | 0.80 |
Autor and Duggan suggest that the value of benefits is increasing relative to current earnings due to the widening distribution of income, but comparing benefits to life-cycle earnings may understate this effect. Chart 2 shows replacement rates based on the new beneficiaries' most recent earnings, specifically the last year of nonzero earnings prior to the onset of disability established by SSA. Replacement rates based on this measure decline until 1981 or 1982, likely in response to phasing in changes from the 1977 amendments for individuals entitled after 1978, but whose onset of disability occurred prior to 1978. After that, the patterns differ from those observed for the AIME formulation. Replacement rates fluctuate after 1985, primarily increasing until 1995 and then generally dropping. There are small increases in the replacement rates for persons entitled to disability in 2000 relative to entitlements in the early 1980s. However, the increases only occur for the median and the highest quartile. The rates vary considerably over time and there is no continuous increase. This evidence could be consistent with a structural rise in replacement rates, but is clearly not persuasive.
Median and quartile replacement rates for newly entitled disabled-worker beneficiaries based on last year of nonzero earnings (indexed to CPI), 1979–2000
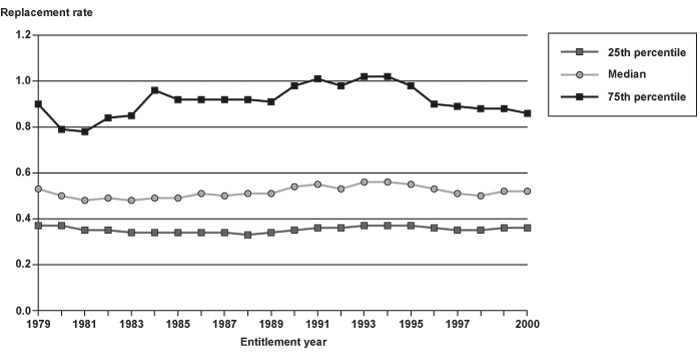
| Entitlement year | 25th percentile |
Median | 75th percentile |
|---|---|---|---|
| 1979 | 0.37 | 0.53 | 0.90 |
| 1980 | 0.37 | 0.50 | 0.79 |
| 1981 | 0.35 | 0.48 | 0.78 |
| 1982 | 0.35 | 0.49 | 0.84 |
| 1983 | 0.34 | 0.48 | 0.85 |
| 1984 | 0.34 | 0.49 | 0.96 |
| 1985 | 0.34 | 0.49 | 0.92 |
| 1986 | 0.34 | 0.51 | 0.92 |
| 1987 | 0.34 | 0.50 | 0.92 |
| 1988 | 0.33 | 0.51 | 0.92 |
| 1989 | 0.34 | 0.51 | 0.91 |
| 1990 | 0.35 | 0.54 | 0.98 |
| 1991 | 0.36 | 0.55 | 1.01 |
| 1992 | 0.36 | 0.53 | 0.98 |
| 1993 | 0.37 | 0.56 | 1.02 |
| 1994 | 0.37 | 0.56 | 1.02 |
| 1995 | 0.37 | 0.55 | 0.98 |
| 1996 | 0.36 | 0.53 | 0.90 |
| 1997 | 0.35 | 0.51 | 0.89 |
| 1998 | 0.35 | 0.50 | 0.88 |
| 1999 | 0.36 | 0.52 | 0.88 |
| 2000 | 0.36 | 0.52 | 0.86 |
So why do the replacement rates for successive cohorts of disability entitlements not demonstrate the increase in replacement rates hypothesized by Autor and Duggan? Other factors such as economic climate or program could also play a role. There are two components to the change in actual replacement rates:
- Structural change—involving changes in SSA's benefit formulation; and
- Behavioral change—involving changes in the beneficiary population caused by various factors, including changes in incentives to apply, in demographics, and in the criteria SSA use to determine disability (for example, the change in mental impairments listings implemented in 1986).14
It is difficult to disaggregate the effects of structural and behavioral change in actual experience. For example: as replacement rates rise, those with high replacement rates have more incentive to apply so, all other things being equal, we would expect to see higher rates as the result of both the structural increase and a behavioral response. The behavioral response reflects the possibility that high–replacement rate applicants could seek and receive benefits, thus raising the observed replacement rates. However, after these high–replacement rate individuals are absorbed by the program, we could see replacement rates for new entitlements begin to decline.
Furthermore, the indexing formula itself may mask the true structural change in replacement rates as the numerator (PIA) and denominator (AIME) are both based on wage-indexed values, hence the increases tend to offset one another and the ratio remains stable (that is, using the AWI to index both the numerator and denominator may, in itself, result in the stability of AIME replacement rates over time as both the numerator and denominator tend to rise by roughly the same proportion).
Estimating the hypothetical replacement rates of those not actually entering the disability rolls may provide a better idea of what is occurring to replacement rates in the absence of program effects associated with screening and other factors.
Methodology
This article examines the effect of indexing using the AWI on Social Security benefits. Two distinct methods of assessing the change in replacement rates over time are applied to those who are insured for disability benefits and could apply. Both methods are used to test the Autor and Duggan hypothesis, and one is also used to quantify the earnings history and bracket effects.
Using the Continuous Work History Sample (CWHS), the distribution of annual earnings is assessed to determine whether there is a widening of the income distribution for those insured for disability benefits and whether low earners are receiving smaller wage increases than others. This will confirm whether the effect hypothesized by Autor and Duggan actually exists. The article also assesses the changes in the proportion of working-age individuals (aged 18–64) who have positive earnings in a given year, to assess the potential effect that excluding nonearners may have on the AWI.
Two methods are used to assess changes in replacement rates over time. Both methods are based on simulations of benefits for disability-insured workers using their actual earnings histories and the benefit formulas in effect in each year over the period 1979–2004.15 The first method, called "hypothetical replacement rates," calculates the actual benefit levels and replacement rates that disability-insured workers would receive if they became disabled over the period 1979 to 2004 to see if these are, in fact, rising. Hypothetical replacement rates are calculated using three alternative earnings measures: lifetime earnings, most recent year of nonzero earnings, and average earnings over the prior 3 years indexed to the CPI.16 The Autor/Duggan hypothesis suggests that replacement rates are increasing relative to workers' present or expected earnings, so the recent earnings measures are key to this analysis.
The second method employs an alternate index that is more representative of the earnings growth of nearly all workers. Analysis of CWHS earnings shows that earnings growth is flat for the lowest 80 percent of earners, and that only the top decile or two produce the widening distribution of earnings. Using this information, a more representative index based on the median earnings growth is used to create a counterfactual for each worker, representing what would happen to the individual's disability benefit if the widening distribution of earnings did not affect the index. This approach also permits one to quantify the "earnings history effect," the "bracket effect," and the combined effect on benefits and replacement rates by decomposing the changes in benefits based on the alternate lifetime earnings calculation and PIA formulation.
Direct comparisons are made between the results from this research using actual earnings histories of disability-insured workers with the hypothetical cases created by Autor and Duggan based on age-specific earnings percentiles generated from historical Current Population Survey data.
The Data
The data employed in this study come from several sources. The indices used in this study come from published sources. The AWI series developed by the Office of the Chief Actuary (OCACT) is used as a measure of mean earnings (SSA 2006a, Table 2.A8). The Consumer Price Index series for Urban Wage Earners and Clerical Workers (CPI-W) is the COLA series used by OCACT to adjust Social Security benefits annually for the change in the cost of living.17 Median earnings data were taken from the historical series of the Annual Statistical Supplement to the Social Security Bulletin (2006a, Table 4.B6). Other series for mean and median earnings were examined and yielded similar results, but limitations on the length of the series led to the above choices for this analysis.
The CWHS is an administrative data file containing a 1 percent sample of all Social Security numbers ever issued. It contains full earnings records enabling the calculation of hypothetical AIMEs and PIAs. It also has information on beneficiary status, allowing the removal of individuals at the time they receive disability benefits. There are two components to the CWHS: the active file and the inactive file. The active file includes all individuals who have ever had earnings or received a benefit. There is also an inactive file for individuals who have never had any activity with SSA. All data used in this article come from the active file. There are three exclusions from the analysis. Workers who actually become disability beneficiaries are dropped from the analysis in the year prior to the year of disability onset. Similarly, workers for whom a date of death appears on the CWHS are dropped from the analysis in the year prior to the year of death.18 Finally, the analysis of replacement rates includes only workers who are insured for disability and are aged 18–61. The age 61 cutoff was used because the majority of workers retire at age 62 and would not have earnings after that age.
Changes in the Earnings Distribution
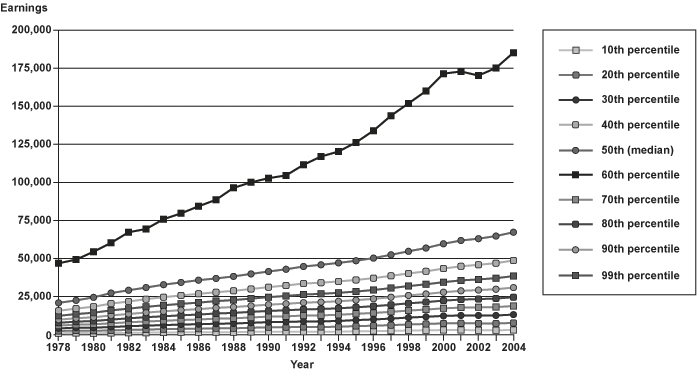
Using the CWHS active file, the earnings distribution was examined for 1978–2004, for individuals aged 18–64 with positive earnings reported during a given year. Chart 3 shows the growth in nominal earnings for each decile and the 99th percentile. There was growth in nominal earnings over the period for each decile. The increasing slope of the earnings line, clearly evident for the 99th percentile and highest decile, suggests greater nominal earnings growth among the highest earners.
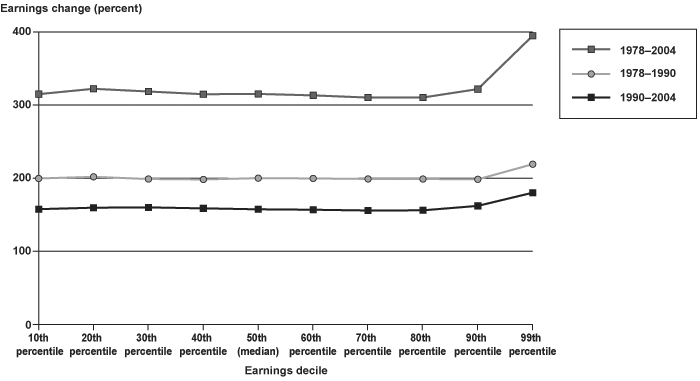
The growth (percentage change) in nominal earnings by decile and 99th percentile is shown in Chart 4 for the entire period (1978–2004) and for two subperiods (1978–1990 and 1990–2004). This chart clearly shows that nominal earnings growth has been relatively equal over the period for deciles up to the 80th percentile, above which high earners (particularly those in the 99th percentile) have had greater earnings growth. The same pattern was present over the two subperiods, indicating that this phenomenon has been occurring for at least a couple of decades. The similarity of growth in nominal earnings across the lowest 80 percent is somewhat surprising as the wage rate has been reported to be declining, at least in real terms, for the lowest earners. However, the CWHS provides only annual earnings, and it is possible that the lowest earners are keeping up by working additional hours or multiple jobs, which would not be reflected in hourly wages.
The CWHS data suggest that the Autor and Duggan hypothesis may be correct, but that the effect is observed for perhaps 80 percent of workers, rather than only the lowest earners.19 Since the growth in nominal earnings over time is relatively constant for all but the highest earners, indexing by average wages could raise the implicit replacement rate for virtually all future beneficiaries. Moreover, the growth in median earnings seems more representative of the "average" worker's earnings growth than the mean. This will be exploited later in the article to quantify the increase in replacement rates.
Average Wage, Median Earnings, and Price Increases
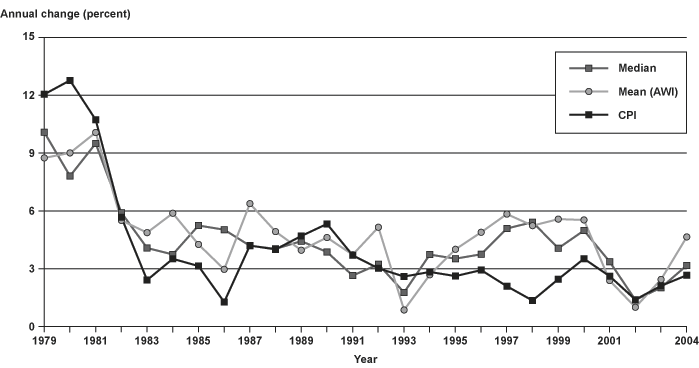
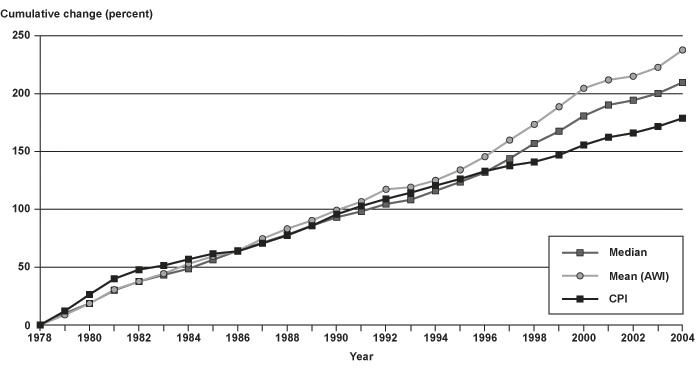
This section makes direct comparisons between the changes over time in measures of average earnings using OCACT's AWI, median earnings from the Annual Statistical Supplement to the Social Security Bulletin (SSA 2006a), and prices using SSA's specific calculation of the CPI.20 Chart 5 shows that the pattern of annual percentage changes in mean and median earnings and prices is not consistent. In some years, the increase in median earnings exceeds the increase in mean wages, but generally the mean wages show the largest increase, followed by median earnings and then prices. Chart 6 shows the cumulative change in the three measures from 1978 through 2004. Over time, generally larger increases in mean wages have led to widening gaps between the mean and median measures. Both earnings measures have increased substantially more than prices over the period, although not in all years.
The Impact of Nonearners on the Mean and Median Earnings Measures
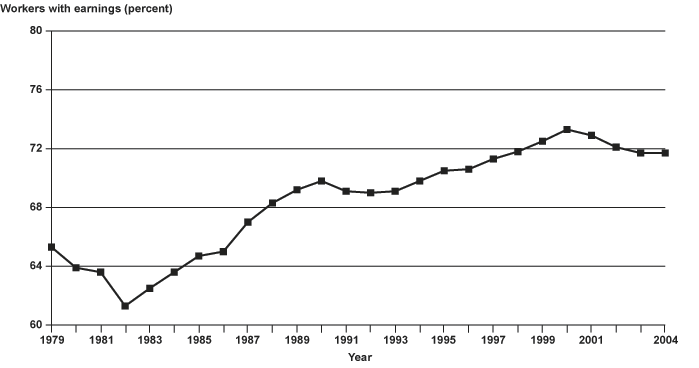
As discussed earlier, the mean and median earnings measures may be biased because nonearners (either due to unemployment or withdrawal from the labor force for a year or longer, or to trends in labor force participation) are excluded from the calculation. Chart 7 shows the percentage of working-aged persons (aged 18–64 in each year) included in the CWHS active file that had positive earnings. The chart shows that the percentage with earnings has been generally trending upward over time. In addition, there are declines in the percentage with positive earnings during periods of recession (the early 1980s, early 1990s, and after 2000). The decline in the percentage with earnings during recessions varies, from only 1 percentage point between 1990 and 1992, to nearly 4 percentage points between 1979 and 1982. The increase in the number of persons without earnings in the year, if included in the calculation, would serve to reduce both the average and the median earnings.21 Thus, excluding individuals who have no earnings in a given year impacts the average wage calculation. Given the upward trend in the proportion of persons with positive earnings over much of the period, it would be difficult to pinpoint the actual number of nonearners to include in the mean and median earnings calculation to establish an alternative population base for calculating the wage index. It also raises questions about how much one would want poor (or good) economic conditions to influence benefit calculations.
Hypothetical Replacement Rates for Disability-Insured Workers
In this section, the CWHS is used to estimate hypothetical replacement rates for disability-insured workers, that is, the replacement rate that would be obtained if a disability-insured nonbeneficiary were to seek benefits. These replacement rates are not susceptible to some of the problems associated with those for new entitlements, such as the effect of changes in SSA screening criteria on new entrants. The measure is, however, subject to the following limitations:
- Absorption onto the disability rolls—if increasing replacement rates induce individuals to leave the labor force for the disability rolls, the replacement rates for nonbeneficiary workers will decline over time.
- Economic cycles—replacement rates based on recent earnings are influenced by economic cycles, though the overall effect is unknown. Low earnings in economic downturns raise replacement rates, and dropping individuals who have no earnings tends to reduce replacement rates, as higher earners generally have more stable employment.
- Underlying demographic shifts over time, such as more women working, women's earnings rising relative to those for men, an aging workforce, and a shift in the age of peak earnings influence the trends in the distribution of replacement rates for cohorts of insured workers.
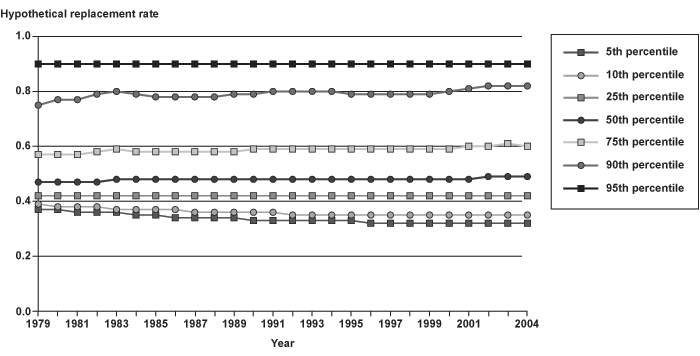
Three measures of hypothetical replacement rates were calculated for each disability-insured worker aged 18–61 in each year 1979–2004. Replacement rates were calculated by dividing the estimated PIA by each of three earnings measures: average lifetime earnings (SSA's AIME), last year of nonzero earnings, and the average of the last 3 years of earnings (CPI indexed).22 Charts 8–10 show replacement rates at selected percentiles (5th, 10th, 25th, 50th, 75th, 90th, and 95th) for the three earnings measures. In Appendix A, Charts A-1 through A-28 show the percentile replacement rates by age.
Chart 8 shows the replacement rate trends for the AIME measure. Hypothetical replacement rates decline for the lowest (5th and 10th) percentiles, and increase for those from the median to the 90th percentile. Appendix Charts A-1 through A-7, which show replacement rates by age, show that AIME replacement rates are dropping for the lowest percentiles, except for those in the youngest age categories. For much of the mid percentiles, replacement rates are fairly stable, as intended by the 1977 legislation, although the younger age groups again show rising replacement rates. In the highest percentiles (90th and 95th), the replacement rates rise for the younger age groups, but tend to decline for the older age groups. The reduction in replacement rates for all but the youngest age group in the 5th and 10th percentiles might be expected because earnings for this high-earning group have been increasing faster than for other groups. Replacement rates for those under age 30 show substantial increases over time at nearly every percentile.23 There is also a slight increase in replacement rates for those aged 30–39. This suggests that either entry-level earnings are declining (because earnings generally are inversely related to replacement rates), individuals are entering the labor force at older ages (after age 22, resulting in additional years with no earnings in the AIME calculation), or individuals are working less.
The relatively small increases in replacement rates for some, and the modest increase for many, suggest that the AIME formulation of replacement rates may support the existence of the Autor/Duggan effect, at least for those with lower lifetime earnings and for some age groups. However, as Autor and Duggan contend that benefits represent a larger portion of current earnings of workers and thus provide incentives to seek disability benefits, formulations of replacement rates based on recent earnings may provide a more accurate picture.
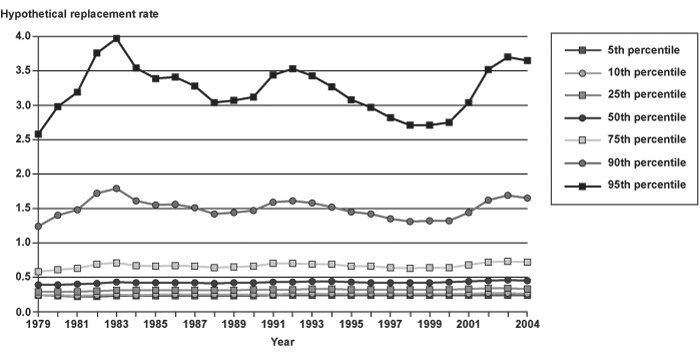
Chart 9 shows the replacement rate trends based on the last year of nonzero earnings. For instance, the estimated PIA for 1980 would be divided by the earnings reported for 1980, or by 1979 earnings if there were none in 1980. The graphs appear relatively stable for the lower percentiles of replacement rates (higher earners) and seem to cycle over time for those with higher replacement rates. When this is broken out by age (Charts A-8 through A-14 in Appendix A), there is a general trend upward in replacement rates, as was suggested by Autor and Duggan, except for those with the highest replacement rates (lowest earnings). Replacement rates based on the last year of earnings rise for the lower replacement rate (high earner) individuals (5th through 75th percentiles). For the lowest earners with high (90th and 95th percentile) replacement rates, it seems that for most age groups the replacement rates seem to rise and fall over time, with a pattern of high replacement rates in periods of poor economic performance (for example, during the recessions of the early 1980s, early 1990s, and after 2000). The one major exception within the 90th and 95th percentiles is the 60–61 age group, which has a definite upward trend in replacement rates. It is interesting that replacement rates for the oldest workers (aged 55–59 and 60–61) increase over the period for most levels, including the highest percentiles. Appendix Charts A-15 through A-21 show the trend graphs for each age group, rather than for percentiles, and more clearly show the increase in replacement rates among the older groups.
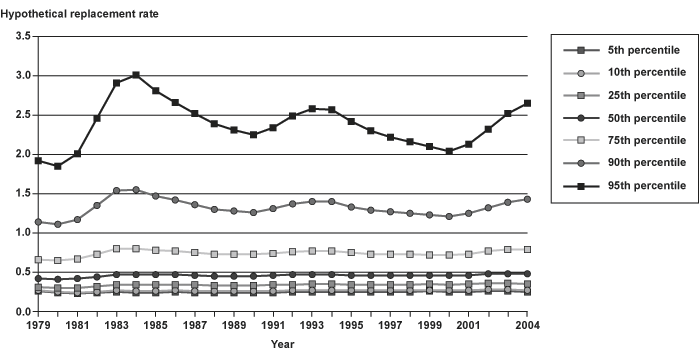
In Charts 10 and A-22 through A-28, replacement rates are based on a measure of recent earnings representing the average earnings of the prior 3 years, price indexed to the year under study. This formulation determines whether examining only 1 year of earnings creates anomalous results. In fact, the trends in replacement rates are nearly identical to those in Chart 9, albeit at a slightly higher rate of replacement. The trends with respect to hypothetical replacement rates for workers are robust, regardless of the measure of recent earnings, and there is some evidence to support the increase in replacement rates that was hypothesized by Autor and Duggan, although it appears to be less prevalent among the lowest earners than they suggest.
How can the results for those with the highest replacement rates (lowest earnings) be explained? First, the lowest earners may fall below the first bend point. With predisability earnings replaced at a constant 90 percent, they would not benefit from the increasing bend points. Also, as noted above, there are serious limitations to an approach using hypothetical replacement rates. If Autor and Duggan are correct and low earners (high replacement rates) are being induced to seek disability benefits as a result of the increase in the value of benefits relative to work earnings, these high–replacement rate individuals could be absorbed into the program over time and no longer be in the base for calculating hypothetical replacement rates, thereby depressing replacement rates over time.24 Demographic shifts may also explain some of the effect. Higher earnings for women should depress replacement rates over time, but other changes such as entering the workforce entry at older ages (Compson 2008) and reaching peak earnings at younger ages could result in higher replacement rates.
Assessing the Autor and Duggan Effect by Exploiting the Stability of Median Earnings
As shown earlier in Chart 4, nominal earnings growth from 1978 to 2004 was constant across at least the lowest 80 percent of earners. This suggests that if the wage index reflected this level of earnings growth, the replacement rate increases associated with the widening earnings distribution would be minimized, although those with earnings in the top 20 percent would suffer replacement rate cuts. In this section, the consistency in earnings growth for the lower 80 percent of workers is exploited in order to quantify the increase in replacement rates and to decompose the increase into the "earnings history" and "bracket" effects identified by Autor and Duggan.
This is accomplished by constructing a median earnings index (MEI),25 which is arguably more representative of the earnings growth for the population as it represents the average earnings growth for over 80 percent of earners and tends to eliminate the effect of the widening distribution of earnings. While there are still individual differences in earnings or wage growth from any index, the median earnings index eliminates the "average" effect of the earnings growth differential from the widening distribution of earnings for the population as a whole. Using each individual as his or her own control, or counterfactual, the worker's replacement rate is calculated using the current AWI formula and a revised formula using the MEI to calculate the AIME and PIA.
The decomposition into changes in replacement rates works as follows:
Total effect = (PIAmei (AIMEmei) – PIAawi (AIMEawi)) / AIMEawi
Bracket effect = (PIAmei (AIMEawi) – PIAawi (AIMEawi)) / AIMEawi
Earnings history effect = (PIAawi (AIMEmei) – PIAawi (AIMEawi)) / AIMEawi
Where:
PIAawi (AIMEawi) is the current law PIA calculated from current-law AIME;
PIAmei (AIMEmei) is the alternate index PIA calculated from the alternate-index AIME;
PIAmei (AIMEawi) is the alternate index PIA calculated from the current-law AIME;
PIAawi (AIMEmei) is the current law PIA calculated from the alternate-index AIME; and
AIMEawi is the current-law AIME and the replacement rate denominator.
The difference in the two formulations is the "total effect" on replacement rates associated with the widening of the distribution of earnings. By using the AWI in the calculation of the AIME, and using the AWI and MEI to calculate the bend points for the PIA, the difference between current-law replacement rates and this formulation is a measure of the "bracket" effect identified by Autor and Duggan. Finally, by using the MEI and AWI to compute the AIME and the AWI in the calculation of the PIA, one obtains an estimate of the "earnings history" effect on replacement rates. It is interesting to note that in nearly all cases (97 percent), the total effect as measured by the difference in the AWI and MEI calculations is equal to the earnings history effect plus the bracket effect. There are very few cases in which the changes interact and there is a discrepancy between the sum of the bracket and earnings history effects and the total effect, and these "errors" are very small.
This approach is not without its weaknesses. As in the hypothetical replacement rate calculation, there is an absorption effect as the high–replacement rate individuals are induced onto the disability rolls and leave the pool of workers in the analysis. However, this approach minimizes demographic shifts in that each case acts as its own control, or counterfactual. Because the measurements are based on lifetime earnings, the impact of economic cycles is also minimized as the replacement rate denominator is less volatile for all but the youngest workers.
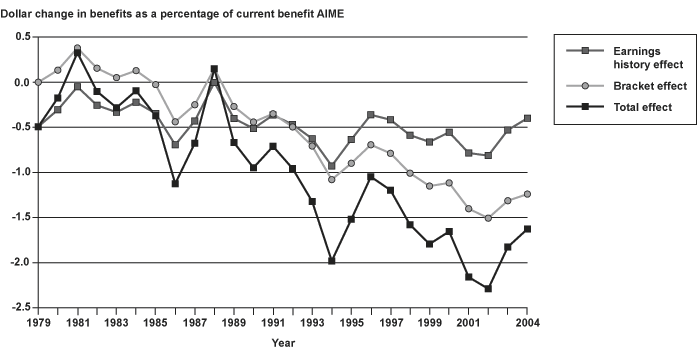
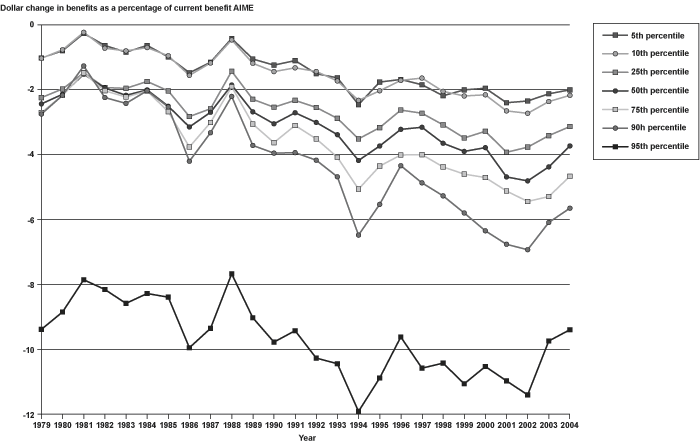
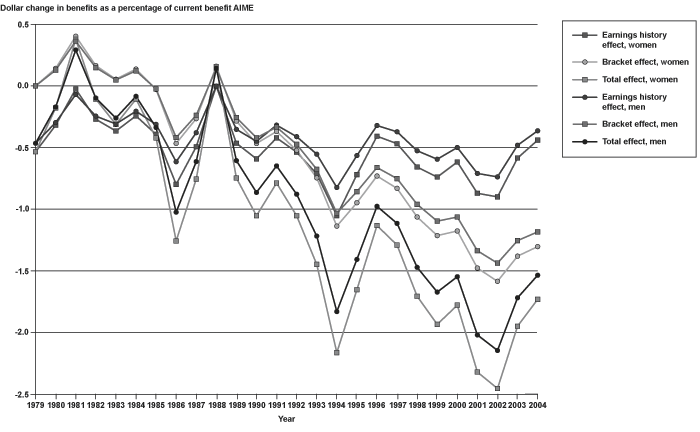
The average effects of the indexing change on replacement rates for the total population are shown in Chart 11. The chart shows a general trend toward greater reductions in replacement rates when using the MEI as a more representative index. The average change is rather small, reaching a maximum reduction in replacement rates of about 2.25 percent of AIME in 2002. The chart also shows that the bracket effect has been the larger contributor to the reduction since the early 1990s, although before then the earnings history effect was larger (and in many years the bracket effect actually resulted in benefit increases).
Total, bracket, and earnings history effects of using alternate indexing to calculate benefits: Mean change in benefits as a percentage of current benefit, 1979–2004
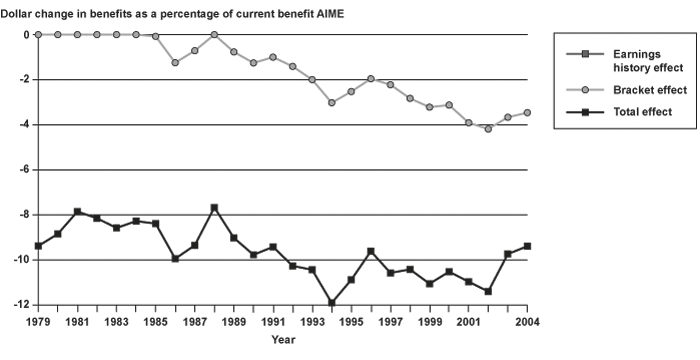
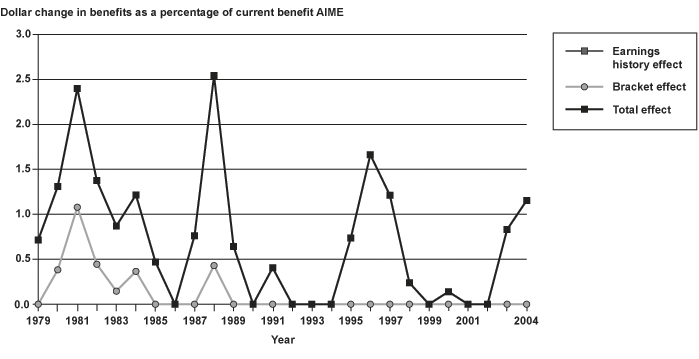
Chart 12 shows the maximum percentage-point reductions in replacement rates resulting from using MEI over the period. These reductions varied from a low of about 8 percent in 1981 and 1988 to a high of about 12 percent in 1994, and the trend is generally toward larger maximum reductions over time. The largest reductions were attributable to the earnings history effect. The maximum increases in replacement rates (Chart 13) were smaller, ranging from no increase to an increase of about 2.5 percent, and showed no distinct trend. In Charts 12 and 13, note that the maximum total effect and the maximum earnings history effect are identical and overlay one another because those with the largest total increases and decreases in replacement rates have the lowest earnings and fall under the first PIA formula bend point and thus cannot have a bracket effect.26
Total, bracket, and earnings history effects of using alternate indexing to calculate benefits: Maximum reductions in benefits as a percentage of current benefit, 1979–2004
Total, bracket, and earnings history effects of using alternate indexing to calculate benefits: Maximum increases in benefits as a percentage of current benefit, 1979–2004
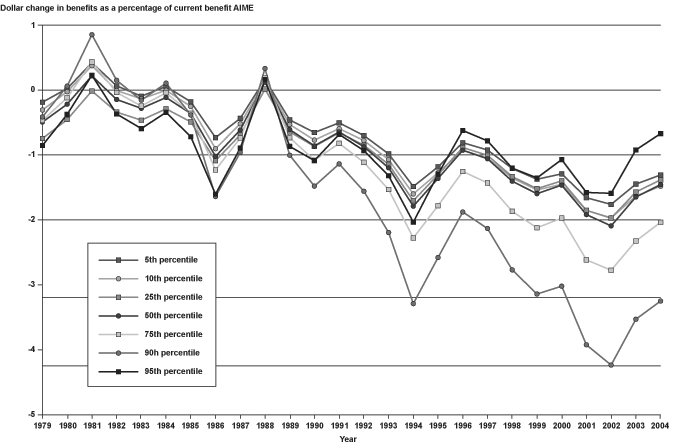
Autor and Duggan hypothesize that implicit replacement rates have increased more for lower earners. This is supported if replacement rates indexed to a more representative measure of earnings growth (in this case, MEI) show decreases from those calculated under the current formula, particularly for lower earners. Chart 11 clearly shows that replacement rates calculated using MEI are lower than current-law rates based on AWI. Chart 14 shows the percentage change from current benefit formulation attributable to using the MEI, by percentile of current-law replacement rates based on the AIME. There is only a slight trend toward larger reductions in replacement rates over time for the very lowest earners (95th replacement rate percentile) and, on average, the 95th percentile had the smallest reductions in average replacement rates in the latter years. However, as Chart 15 shows, the 95th percentile included individuals with the largest maximum reductions in replacement rates, varying between 8 percentage points and 12 percentage points over the period. Clearly the very lowest earners are an anomaly. This may be because many of these individuals have benefits that are below the first bend point in the PIA formula and thus are unaffected by the "bracket effect."
Total effect of using alternate indexing to calculate benefits: Mean change in benefits as a percentage of current benefit, for selected current replacement rate percentiles, 1979–2004
Total effect of using alternate indexing to calculate benefits: Maximum reduction in benefits as a percentage of current benefit, for selected current replacement rate percentiles, 1979–2004
Excepting the results for those at the 95th percentile, the average reduction in replacement rates shown in Chart 14 was generally larger for those in the higher replacement rate categories (lower earnings), and all percentiles show strong trends toward lower replacement rates over time under the alternate indexing formula. The average reductions in replacement rates were largest for those in the 90th replacement rate percentile, and the size of the reductions tended to increase over time. There were smaller average reductions for lower replacement rate percentiles. Interestingly, unlike the prior analysis, the peaks in replacement rates do not coincide with economic recessions.27
This analysis of alternative replacement rate formulations does not seem to provide strong support for Autor and Duggan's hypothesis that wage indexing has a greater effect on the lowest earners. The earlier approach, analyzing hypothetical replacement rates based on recent earnings, led to a similar finding. However, examining the maximum reduction in replacement rates by percentile (Chart 15) reveals that the largest reductions for individuals occur in the highest replacement rate category—that is, for the lowest earners. This indicates that the incentives created by increased replacement rates may be greatest for some of the lowest earners. Moreover, the maximum reductions in replacement rates decline as the level of replacement rates falls (that is, they are smaller for those with higher earnings).
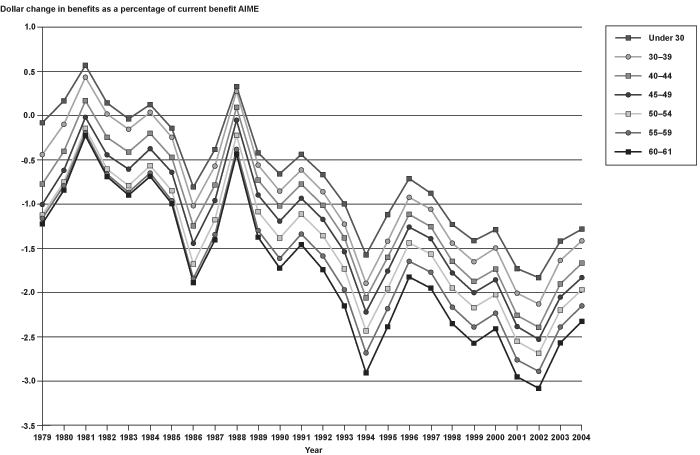
The alternate replacement rate formulation was also examined to assess differences by age. The first approach, hypothetical replacement rates, showed increased replacement rates for all age groups, with a particularly large increase for lower earners aged 60–61. This is confirmed by the alternate indexing approach (Chart 16). Recall that a decline in MEI replacement rates relative to AWI indicates an implicit rise in current-law rates. Those aged 60–61 had the largest reduction in replacement rates under the alternate formulation, but the difference between this and the other age groups was considerably smaller than that found when using the hypothetical replacement rate approach. The latter result may be due to changes over time in the age of peak earnings for successive cohorts, which the alternate indexing approach minimizes.
Total effect of using alternate indexing to calculate benefits: Mean change in benefits as a percentage of current benefit, by age group, 1979–2004
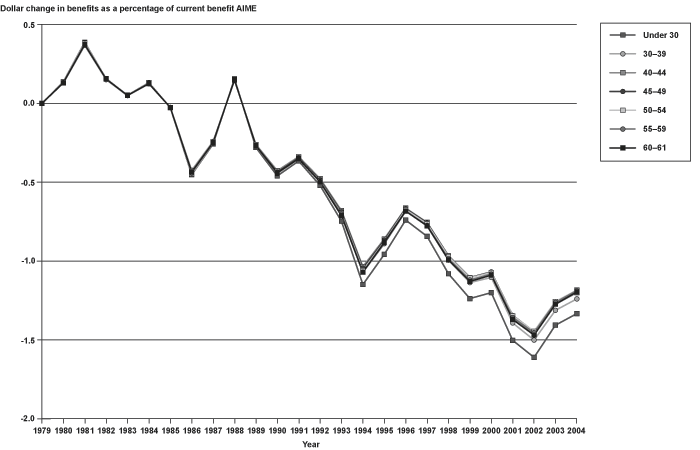
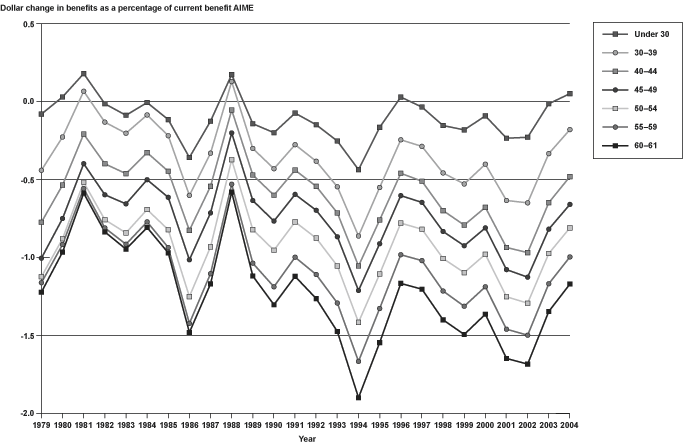
In decomposing the total effect into the bracket and earnings history effects, the analysis shows that the trend toward higher replacement rates is produced by the bracket effect (Chart 17), while the larger reductions for older workers (larger increase in replacement rates under current law) is attributable to the earnings history effect (Chart 18). Moreover, there is very little trend to the earnings history effect; it seems to cycle, but not synchronously with economic cycles.
Bracket effect of using alternate indexing to calculate benefits: Mean change in benefits as a percentage of current benefit, by age group, 1979–2004
Earnings history effect of using alternate indexing to calculate benefits: Mean change in benefits as a percentage of current benefit, by age group, 1979–2004
The changes in replacement rates for men and women are shown in Chart 19. Women have larger reductions in replacement rates under the alternate MEI formula, and hence have been benefiting more from the implicit increase in replacement rates. This is likely because women tend to have lower earnings and thus higher replacement rates than men, and those with higher replacement rates tend to have larger reductions.
Total, bracket and earnings history effects of using alternate index to calculate benefits: Mean change in benefits as a percentage of current benefit, by sex, 1979–2004
Comparisons to Autor and Duggan Results
In Table 2 of their "Crisis" article, Autor and Duggan (2006) provide estimates of replacement rate changes for men between 1984 and 2002 based on the overall distribution of earnings. Table 1 below provides similar estimates based on the calculations in this article. As with Autor and Duggan (2006), which bases its estimates on age-specific percentiles of earnings, the calculations in Table 1 are based on replacement rates for individuals by age-specific percentiles of lifetime earnings (AIME). Because the replacement rates based on recent earnings are so volatile,28 the median replacement rate for individuals whose AIME is within 5 percent (plus or minus) of the percentile value of AIME was used (see the data table appendix available in the online version of this article for a more detailed data presentation).
| Calculation | Replacement rates (percent) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10th percentile | 50th percentile | 90th percentile | |||||||
| 1984 | 2002 | Change | 1984 | 2002 | Change | 1984 | 2002 | Change | |
| Ages 30–39 | |||||||||
| Autor and Duggan | 48.4 | 59.4 | 11.0 | 36.2 | 41.9 | 5.7 | 24.1 | 26.1 | 2.0 |
| Hypothetical rates, last year earnings a | 59.0 | 63.0 | 4.0 | 37.0 | 41.0 | 4.0 | 25.0 | 28.0 | 3.0 |
| Hypothetical rates, last 3 years earnings b | 69.0 | 65.0 | -4.0 | 39.0 | 42.0 | 3.0 | 27.0 | 29.0 | 2.0 |
| Hypothetical rates, lifetime earnings c | 55.0 | 64.0 | 9.0 | 43.0 | 46.0 | 3.0 | 34.0 | 35.0 | 1.0 |
| Alternate index | … | … | 3.0 | … | … | 1.6 | … | … | 1.8 |
| Ages 40–49 | |||||||||
| Autor and Duggan | 51.1 | 55.1 | 4.0 | 33.5 | 43.3 | 9.8 | 19.4 | 24.8 | 5.4 |
| Hypothetical rates, last year earnings a | 50.0 | 56.0 | 6.0 | 34.0 | 42.0 | 8.0 | 24.0 | 26.0 | 2.0 |
| Hypothetical rates, last 3 years earnings b | 56.0 | 58.0 | 2.0 | 36.0 | 42.0 | 6.0 | 25.0 | 27.0 | 2.0 |
| Hypothetical rates, lifetime earnings c | 50.0 | 57.0 | 7.0 | 41.0 | 43.0 | 2.0 | 35.0 | 31.0 | -4.0 |
| Alternate index | … | … | 2.6 | … | … | 1.8 | … | … | 1.7 |
| Ages 50–61 | |||||||||
| Autor and Duggan | 55.2 | 64.0 | 8.8 | 34.7 | 45.9 | 11.2 | 19.0 | 23.7 | 4.7 |
| Hypothetical rates, last year earnings a | 50.0 | 55.0 | 5.0 | 36.0 | 44.0 | 8.0 | 23.0 | 26.0 | 3.0 |
| Hypothetical rates, last 3 years earnings b | 56.0 | 57.0 | 1.0 | 37.0 | 44.0 | 7.0 | 24.0 | 27.0 | 3.0 |
| Hypothetical rates, lifetime earnings c | 51.0 | 54.0 | 3.0 | 42.0 | 40.0 | -2.0 | 38.0 | 31.0 | -7.0 |
| Alternate index | … | … | 2.5 | … | … | 1.9 | … | … | 1.7 |
| SOURCES: Autor and Duggan (2006) and author's calculations based on Continuous Work History Sample data. | |||||||||
| NOTE: … = not applicable. | |||||||||
| a. Replacement rates based on CPI-indexed last year of nonzero earnings. | |||||||||
| b. Replacement rates based on CPI-indexed average of last 3 years of earnings. | |||||||||
| c. Replacement rates based on lifetime earnings (average indexed monthly earnings). | |||||||||
This article uses actual earnings histories of disability-insured workers to compute replacement rates based on recent earnings. Table 1 shows that the results of this approach are generally consistent with Autor and Duggan's use of historical percentiles of earnings, although the effects estimated here are generally somewhat smaller than those estimated by Autor and Duggan, at least in the two older age groups.29 Replacement rates based on lifetime earnings (AIME) are also shown and, despite the congressional intent to stabilize replacement rates, the youngest group (aged 30–39) and lowest earners (10th percentile of age-specific AIME) see replacement rates increase over time. The result for men aged 30–39 is consistent with earlier analysis; however, the AIME replacement rates for the 10th percentile of AIME (the high replacement rate percentiles) seem to be fairly stable overall in the earlier analysis (Chart 8), perhaps indicating a difference between men and women.
The alternate index does not produce directly analogous results to those generated by Autor and Duggan, but change over time can be estimated using a difference-in-differences approach using the estimates of the "total effect" on replacement rates for 1984 and 2004. This measure also shows replacement rates rising over time, although with very small differences by age. Interestingly, using this approach, the lowest earners (10th percentile) receive greater increases than those in the 50th and 90th percentiles, which was not the case with hypothetical replacement rates for recent earnings. The use of lifetime earnings as the basis for this measure may have helped stabilize replacement rates both for individuals who were dropped from the calculation of the last year of earnings because of intermittent labor force participation and years with no earnings, and for persons whose last year of earnings may have produced extreme replacement rate values.
Conclusions
Hypothetical replacement rates and an alternate indexing formulation (MEI) both seem to show that using the AWI has led to increases in replacement rates for a large portion of workers. Hypothetical replacement rates based upon recent earnings show replacement rate increases that are generally somewhat larger for those in the middle of the earnings distribution. Using the alternate index approach, lower earners tend to have slightly larger increases in replacement rates than middle and upper earners. Both methods support Autor and Duggan's hypothesis that there has been an implicit increase in replacement rates due to the widening distribution of earnings, and this analysis suggests that replacement rates have risen for large portions of the workforce. The lowest 5 percent of earners have relatively small increases—an expected result, as the lowest earners may fall below the first bend point in the PIA formula, benefiting from the "earnings history" effect but not from the "bracket" effect.
Based on the alternate indexing method, the increases in replacement rates over this extended period of analysis have been relatively small, averaging about 2 percentage points of AIME in recent years. Benefits themselves have increased about 6 percent over what they would have been had a more representative index, or a more equal distribution of earnings prevailed. Hypothetical replacement rates based on recent earnings suggest larger increases than other measures, especially for moderate earners. The decomposition suggests that the "bracket" effect produces the trend toward lower replacement rates, although the "earnings history" effect reduces replacement rates for all cohorts.
This analysis strongly suggests the effects on replacement rates are smaller than those estimated by Autor and Duggan. In fact, the impact over time on replacement rates for those of advanced age (that is, aged 60–61) seems to be as large, or perhaps larger, than the impact of the change in the earnings distribution. The increase in replacement rates for the lowest earners (highest replacement rate percentiles) seems to be smaller than that observed for some other levels of earnings. Overall, the magnitude of the increases in replacement rates, on average, does not seem to offer large incentives to leave work for disability benefits, although results show there are some individuals for whom the increases are much larger (as measured by the maximum changes to replacement rates). The impact of advanced age, as mentioned above, does suggest the effect identified by Autor and Duggan may induce more individuals to retire early and take reduced retirement benefits.
The extent to which this trend toward higher implicit replacement rates continues depends on a number of factors, including a continued widening of the distribution of earnings. Another potential factor is the amount of income that is considered in the average wage index and median earnings calculations. Recent changes have excluded health insurance premiums and money paid into pretax spending accounts for medical and child care expenditures. These changes could result in a narrowing or a widening of the distribution of earnings, depending on the behavioral response at various levels of earned income.
Implications for Policy
The foregoing analysis suggests that Autor and Duggan are correct in their hypothesis that replacement rates are rising due to the widening distribution of income, although the increase may not be as great as their estimates suggested. This finding is important for a number of reasons, perhaps most importantly because it has implications for solvency and policy proposals that have been made to address Social Security's future. It is necessary to consider the impact of wage indexing both from a program cost perspective and from a behavioral perspective where individual incentives could be further distorted. This section will discuss some of the implications of the current AWI indexing and the increase in replacement rates in the context of solvency and policy proposals.
A number of solvency proposals have focused on altering the indexing of earnings in the benefit formula. One proposes replacing the AWI with the CPI to index earnings, which would achieve solvency but would also result in falling replacement rates over time. Progressive indexing has also been proposed, under which earnings below a threshold level are wage indexed, and earnings above that threshold are price indexed. Progressive wage indexing would continue the implicit replacement rate creep identified by Autor and Duggan for those low earners subject to wage indexing. This could continue to increase incentives for these low earners to seek disability benefits (or to retire at earlier ages).
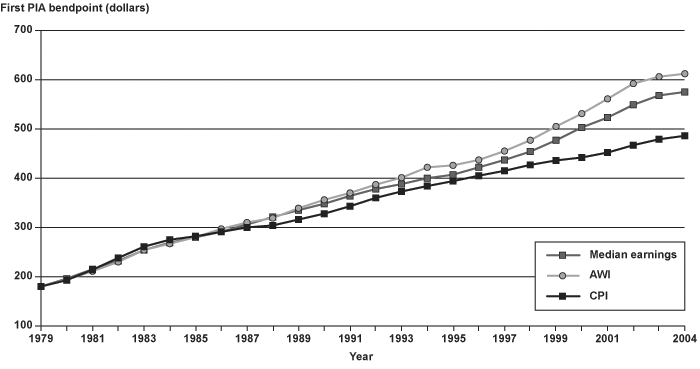
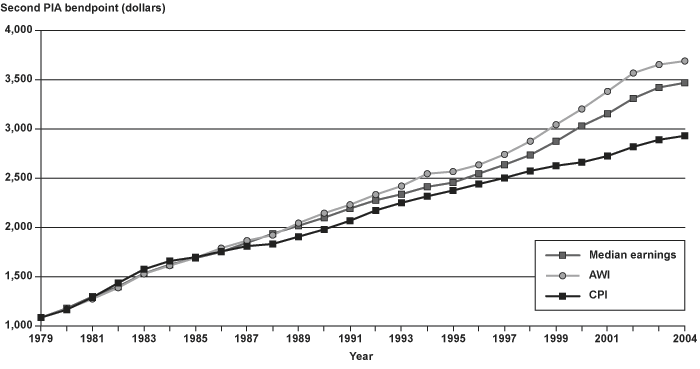
Charts 20 and 21 show the first and second bend points in SSA's wage-indexed values30 of the formula to calculate the primary insurance amount (PIA), the base benefit for disabled and retired workers, for 1979–2004. In addition to those based on the AWI, bend points based on the CPI and on median earnings are also calculated. The charts clearly show that the bend points increase more rapidly under average wage indexing than they would if they were price indexed. Indexing the bend points to the growth in median earnings would slow the increase in the bend points and help to reduce the implicit increase in replacement rates identified by Autor and Duggan.
Table 2 summarizes changes to the bend points for the PIA calculation over the period 1979–2004. Bend points indexed to median earnings would be 6 percent lower in 2004 than the current AWI bend points. Benefits at the first bend point based on a MEI would be about 5 percent lower than those under current law, and benefits at the second bend point would be about 2.5 percent lower. The reduction in bend points based on median earnings is about 30 percent of the bend point reduction that would result from using the CPI.
| Indexing formula | First bend point (dollars) | Second bend point (dollars) | Percentage reduction b in bend point | Benefit reduction b for earnings up to first bend point (dollars) | Benefit reduction b for earnings up to second bend point (dollars) |
|---|---|---|---|---|---|
| Current (AWI) | 612 | 3689 | … | … | … |
| Median earnings | 575 | 3468 | 6 | 33.30 | 92.18 |
| CPI | 486 | 2930 | 20.6 | 113.40 | 315.96 |
| SOURCE: Author's calculations using historical series from SSA (2008). | |||||
| NOTES: … = not applicable; PIA = primary insurance amount; AWI = average wage index; CPI = consumer price index. | |||||
| a. Bend point calculations for alternate indexing formulas assume those formulas would have been in effect for the period 1979–2004. These bend points would apply to 2006 entitlements. | |||||
| b. Relative to AWI. | |||||
The foregoing analysis suggests that the AWI tends to overcompensate most workers relative to their actual earnings gains and results in higher replacements rates for successive cohorts. The growth in median earnings has been more representative of earnings growth over the past 2 decades for 80 percent (or more) of earners, and indexing by median earnings growth would modestly reduce replacement rates for virtually all workers. The analysis suggests that employing a MEI could help stabilize replacement rates, reduce incentives to seek disability benefits and early retirement benefits, and lower the long-term funding deficit. A byproduct of changing from the AWI to a slower growing index such as median earnings would be a corresponding reduction in the increases to the taxable maximum. Thus the effect of reducing benefits could be somewhat offset by smaller tax receipts from the highest earners. This effect could be reduced or eliminated in several ways. For example, some Social Security reform proposals have suggested changing the taxable maximum to establish a set percentage of the wage base to be taxed. One proposal seeks to return the percentage of the wage base subject to taxation to the level that was in place at program inception. At that time, as well as after the 1983 reforms, 90 percent of the wage base was taxed for Social Security purposes, while only 85 percent of the wage base is taxed today (Reno and Lavery 2005). If 90 percent of the wage base were taxable, the estimated taxable maximum for 2006 would have been around $150,000, rather than the $94,200 maximum under current law.
Changing to an alternate indexing formulation could help long-term financing issues without some of the problems associated with other proposed solutions. For example, using CPI to index the benefit formula and the earnings history would reduce replacement rates for successive cohorts of entitlements (as long as earnings grow faster than prices). Progressive indexing, which would index a portion of earnings to wages and the remaining earnings to CPI, would serve to perpetuate the implicit replacement rate creep as discussed above. (Progressive indexing based on the MEI and CPI, rather than the AWI and CPI, would help overcome this problem.) Using the MEI would retain current equity in benefits across earnings levels, have only a small impact on adequacy (successive cohorts would still benefit, at least partially, from higher living standards), and address issues of the incentives associated with increasing replacement rates.
Future Research
Additional research could examine recent disability benefit applicants or awardees to assess whether individuals with larger replacement rate increases (or who would have had larger reductions in benefits from the alternate calculation) were more likely to apply than others in their cohort. This could help clarify the behavioral effect of higher implicit replacement rates on increases in applications and awards, which are the source of the "crisis" suggested by Autor and Duggan. This research would also help assess the impact of the absorption of persons with high replacement rates on the foregoing analysis.
Another obvious extension of this work is to examine the changing incentives for those eligible for early retirement at age 62. The results are expected to be comparable to those obtained in this article for workers aged 60–61, which had a striking trend toward higher disability replacement rates over time. The analysis revealed trends for this age group that were consistent with the Autor and Duggan hypothesis, and of greater magnitude than for other age groups. The results suggest that changing the indexing method for retirees would reduce benefits, increasing incentives to continue in the labor force rather than seek early retirement. This would improve long-term solvency.
SSA may want to monitor the effects of average wage indexing on the benefit formula and the taxable maximum. Further work could also assess the impact of recent changes, such as the exclusion of health insurance premiums and money paid into pretax spending accounts for medical and child care expenditures, on earnings at various earnings percentiles, and to determine the effects on replacement rates. SSA does not currently receive information about earnings reductions due to the pretax payments under these plans, but this information may become available in the future.
Notes
1 The switch from the old method of calculating benefits to the new decoupled benefit created the infamous "notch baby" problem.
2 For additional discussion of the AWI and decoupling see Donkar (1981).
3 The replacement rate is the ratio of the Social Security disability benefit to a measure of predisability earnings and represents the share of predisability earnings replaced by Social Security benefits.
4 See, for example, U.S. Senate Committee on Finance (1977, 176). John C. Danforth discusses his preference for CPI indexing of earnings to avoid increases over time in the real benefits paid to cohorts of retirees and points out that "while wage indexing only cuts the long-range deficit in half, price indexing reduces the deficit totally, placing the system in long-range actuarial balance."
5 The wage index measures earnings of workers who are employed by others, and excludes the self-employed. The earnings index includes both categories of workers.
6 The year of eligibility is the year of attainment of age 62 for retirement benefits, the year of disability entitlement for disability benefits, or the year of death for survivor's benefits.
7 For more specific information on the National Average Wage Index see http://www.socialsecurity.gov/OACT/COLA/AWI.html.
8 The worker may have benefits recalculated if subsequent earnings result in a higher benefit amount, although the base year of wage indexing is left unchanged.
9 There is a special formula for computing the maximum benefits payable to the family of a disabled worker. The family maximum for a family of a disabled worker is 85 percent of the worker's AIME. However, it cannot be less than the worker's PIA nor more than 150 percent of the PIA.
10 These are considered to be "near-current" wage levels because the base year for wage indexing is 2 years prior to the date of eligibility.
11 The effect may be attenuated for disabled workers due to their shorter earning history and generally lower earnings.
12 Similarly, for older low earners, the higher implicit replacement rates may encourage earlier retirement.
13 This effect will create year-to-year differences in implicit replacement rates, but may also influence the trend over time if there is a long-term trend in labor force participation that is correlated with earnings, such as the increase in labor force participation by women over this period.
14 For additional discussion of changes influencing the disability rolls, see SSA (2006b).
15 This was based strictly on the calculation of the worker's AIME and PIA. The $122 minimum benefit in effect from 1979–1981 was not included, nor was the special minimum. Neither minimum benefit affected many beneficiaries and their effects diminished over the period under study. Thus, including these alternative benefit amounts would likely overstate the impact indexing had on replacement rates.
16 For the last year of earnings measure, if the earnings in the last year prior to the hypothetical onset were zero, the year prior was used. If the last year of nonzero earnings was more than 2 years before disability onset, the observation was dropped. For the average of the last 3 years of earnings, zeroes were included in the calculation, unless earnings in all 3 years were zero, in which case the observation was dropped. In all, only 5.7 percent of the observations were dropped for the last year of nonzero earnings measure, and 3.5 percent were dropped from the last 3 years of earnings measure. This small number of reductions for the lack of recent earnings likely reflects the prior exclusion of cases for not meeting the requirement of being insured for disability in each observational year.
17 For a description of COLA calculation, see http://www.socialsecurity.gov/OACT/COLA/latestCOLA.html. For the COLA Series, see http://www.socialsecurity.gov/OACT/COLA/colaseries.html.
18 The CWHS is linked to SSA death records, and while nearly all deaths are reported to SSA, not all are and there may be a small number of deaths that could not be excluded from this analysis. Due to the fact that to be insured for disability one must have 10 quarters of coverage during the prior 20 quarters, these individuals will not remain in the analysis for more than 5 years.
19 In their first paper, Autor and Duggan looked at data for the lowest decile of earnings to support their contention. In their latter paper there was a wider focus, which considered the 10th, 50th, and 90th percentiles of earnings. Direct comparisons are made later in this article.
20 When making cost-of-living adjustments, SSA uses a specific formulation based on BLS's CPI using the year-over-year change in the average of the 3 months of the 3rd calendar quarter. For specifics of SSA's COLA calculation see http://www.socialsecurity.gov/OACT/COLA/latestCOLA.html.
21 On the other hand, the reentry of marginal workers during better economic times could tend to hold down the increase in mean and median earnings.
22 For the last year of earnings measure, if there are no earnings in the prior 2 years, the observation is dropped. For the average of the last 3 years of earnings, if earnings in all 3 years were zero, the observation was dropped.
23 Replacement rates are flat in the 90th and 95th percentiles for those under 30 because the benefit formulation caps replacement rates for low AIME workers at 90 percent.
24 On the other hand, Figure 1 shows little evidence of successively higher replacement rates for cohorts of entitlements over this period.
25 The median earning measure was chosen due to the availability of a published series going back to 1937 (SSA 2008, Table 4.B6). A median wage index could be employed instead and a limited series of median wages (net compensation) is available from the Office of the Chief Actuary (http://www.socialsecurity.gov/OACT/COLA/central.html). A sensitivity analysis was done with the more limited time frame (1990–2004) and there was little difference in the indexing results based on median earnings (used in this article) and median wages.
26 See, for example, Chart 15, which shows the 95th percentile of AIME replacement rates have the largest reductions. See also Chart 8: there, note that the 95th percentile of AIME replacement rates consistently has a replacement rate of .9, indicating that these individuals are below the first bend point and cannot have a bracket effect.
27 The fact that replacement rates do not cycle with economic conditions is likely because this analysis does not rely solely on recent earnings levels (which are influenced greatly by economic cycles) and the approach does not suffer from certain limitations associated with the hypothetical replacement rate analysis.
28 See Appendix B, Table B-15, in the online version of this article at http://www.socialsecurity.gov/policy/docs/ssb/v68n3/v68n3p1_app.html.
29 The use of hypothetical earnings histories assuming that an individual remains in the same earnings percentile for a lifetime likely results in an upward bias. Since wages generally grow over the individual's lifecycle, the higher earnings will result in lower replacement rates.
30 Note that the bend points are indexed to 2 years prior to age 62 for retirees and 2 years prior to entitlement for disabled persons. Thus the bend points based on 2004 would apply to 2006 disability entitlements.
References
Autor, David H., and Mark G. Duggan. 2003. The rise in the disability rolls and the decline in unemployment. Quarterly Journal of Economics 118(1): 157–205.
———. 2006. The growth in the Social Security disability rolls: A fiscal crisis unfolding. Journal of Economic Perspectives 20(3): 71–96.
Compson, Michael. 2008. Estimating the first instance of substantive covered earnings in the labor market. Research and Statistics Note No. 3008-04. Available at http://www.socialsecurity.gov/policy/docs/rsnotes/rsn2008-04.pdf.
Donkar, Eli. 1981. Average wages for indexing under the Social Security Act and the automatic determinations for 1979–1981. Actuarial Note No. 103. Washington, DC: SSA.
Muller, L. Scott, and Jennifer Lee. 2004. Actual replacement rates for newly entitled disabled worker beneficiaries first entitlements to disability: 1970–2000. SSA unpublished manuscript.
Reno, Virginia, and Joni Lavery. 2005. Options to balance Social Security funds over the next 75 years. Social Security Brief No. 18. Washington, DC: National Academy of Social Insurance.
[SSA] Social Security Administration. 2006a. Annual statistical supplement to the Social Security Bulletin, 2005. Washington DC: Office of Policy, Office of Research, Evaluation, and Statistics.
———. 2006b. Trends in the Social Security and Supplemental Security Income disability programs. Washington DC: Office of Policy, Office of Research, Evaluation, and Statistics.
———. 2007. Measures of central tendency for wage data. Baltimore, MD: Office of the Chief Actuary. Available at http://www.socialsecurity.gov/OACT/COLA/central.html.
———. 2008. Annual statistical supplement to the Social Security Bulletin, 2007. Washington DC: Office of Retirement and Disability Policy, Office of Research, Evaluation, and Statistics.
U.S. Congress. Senate Committee on Finance. 1977. Report on H.R. 5322 Social Security Amendments of 1977. Report No. 95-572.
Bibliography
Biggs, Andrew G., Jeffrey R. Brown, and Glenn R. Springstead. "Alternative Methods of Price Indexing Social Security: Implications for Benefits and System Financing." National Tax Journal 58, no. 3 (2005): 483–504.
Congressional Research Service. Indexation of Federal Programs. Report prepared for the Senate Committee on the Budget. Washington, DC: Government Printing Office, 1981.
Government Accountability Office. Social Security Reform: Implications of Different Indexing Choices. Report No. GAO–06–804. Washington, DC: GAO, 2006.
Gottschalk, Peter, and Sheldon Danziger. Inequality of Wage Rates, Earnings, and Family Income in the United States, 1975–2002. Population Studies Center Report No. 04-568. Ann Arbor, MI: Institute for Social Research, University of Michigan, 2004.
Kestenbaum, Bert. Primary Insurance Amount for an Average Male Worker. Actuarial Note No. 121. Washington, DC: Department of Health and Human Services, Social Security Administration, Office of the Actuary, 1984.
Kopczuk, Wojciech, Emmanuel Saez, and Jae Song. Uncovering the American Dream: Inequality and Mobility in Social Security Earnings Data since 1937. NBER Working Paper No. 13345. Cambridge, MA: National Bureau of Economic Research, 2007. Also available online at http://www.nber.org/papers/w13345.
Leimer, Dean R. The Role of the Replacement Rate in the Design of the Social Security Benefit Structure. Staff Paper No. 36. Washington, DC: Department of Health, Education, and Welfare, Social Security Administration, Office of Policy, Office of Research and Statistics, 1979.
Levy, Frank, and R. J. Murnane. "U.S. Earnings Levels and Earnings Inequality: A Review of Recent Trends and Proposed Explanations." Journal of Economic Literature 30, no. 3 (1992): 1333–1381.
Munnell, Alicia, and Mauricio Soto. What Does Price Indexing Mean for Social Security Benefits? Just the Facts on Retirement Issues No. 14. Boston, MA: Center for Retirement Research, Boston College, 2005.
Social Security Administration. Provisions that Could Change the Social Security Program. Baltimore, MD: Office of the Chief Actuary, 2008. http://www.socialsecurity.gov/OACT/solvency/provisions/index.html.
U.S. Congress. House. Committee on Ways and Means. Social Security Amendments of 1977. 95th Congress, 1st session, 1977. H. Rep. 837.
U.S. Congress. Senate. Committee on Finance. Social Security Amendments of 1977. 95th Congress, 1st session, 1977. S. Rep. 612.