Literature Review of Long-Term Mortality Projections
Social Security Bulletin, Vol. 66, No. 1, 2005
The Board of Trustees of the Federal Old-Age and Survivors Insurance and Disability Insurance (OASDI) Trust Funds reports on the current and projected future financial status of the trust funds annually. The Trustees project trust fund finances 75 years into the future. Mortality is one key demographic assumption that feeds into these long-range projections. This article reviews a range of predictions about long-term mortality improvement and assesses where the Trustees' 75-year mortality projection falls within this range. In general, the predictions of future mortality declines in the 2004 Social Security Trustees Report tend to be in the mainstream of professional actuarial and international official government opinion and to be lower than the majority of the small group of demographers who produce comparable estimates.
Hilary Waldron is with the Division of Economic Research, Office of Research, Evaluation, and Statistics, Office of Policy, Social Security Administration.
Acknowledgments: Thanks to Edward DeMarco, Paul Hewitt, Joyce Manchester, Paul Van de Water and Alice Wade for helpful comments and suggestions on various versions of this paper. The author also wishes to thank John Wilmoth for generously providing an early draft of his working paper in advance of its publication.
The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Overview
Predicting life expectancy 75 years into the future today is equivalent to having a forecaster in 1929 predict life expectancy for 2004. The most accurate prediction about such a forecast is probably that it will be wrong. Each forecast in this review involves assumptions about the extent to which the past will represent the future and the appropriate definition of the relevant past. Most demographers who produce forecasts prefer to fit a trend line to historical data, treating fluctuations in gains in life expectancy as random fluctuations around an upwardly trending mean. Most actuaries prefer to adjust past trends based on their interpretations of the causes of these past trends and the likelihood of these past events being repeated in the future. In addition, some experts in the field of aging believe that the pace of mortality decline will slow down because of the biological limits of the human body; others believe that science can overcome current limits to life expectancy. Some experts believe that changes in lifestyle and the adoption of healthier behaviors could increase life expectancy significantly, even without further medical breakthroughs.
This literature review compares the 2004 forecasts of the Board of Trustees of the Old-Age and Survivors Insurance and Disability Insurance (Social Security) Trust Funds with the recommendations of the 1999 and 2003 Technical Panels on Assumptions and Methods, both of whom use age-specific extrapolation techniques to recommend faster mortality improvement. The review then examines the recommendations of researchers who use life-expectancy extrapolation techniques to forecast convergence in life expectancies among developed nations. These researchers recommend even faster mortality improvements for the United States than do the two most recent technical panels. Finally, the review provides an overview of arguments in favor of a forecast that incorporates a theoretical maximum achievable life expectancy. These arguments generally imply a slowdown in the rate of mortality decline as the theoretical maximum life expectancy is reached. Studies by these experts are not directly comparable, but they are relevant to the extent that they contradict the assumptions of demographers, actuaries, and other forecasters who do not force their models to project only up to a theoretical maximum life span. Because the views of biomedical researchers who predict extremely large mortality declines are more speculative in that their predictions rely on large future medical breakthroughs to be achieved, they are not examined in this review.
A determination of where the Social Security Trustees' mortality forecast lies within the range of opinions about future gains in life expectancy largely depends on which opinions are included in the range. Philosophically, those who predict the least amount of future gains in mortality reduction are probably those who believe that the biological limits of the human body (or senescence) will cause average life expectancy to eventually run into a maximum limit (Fries [1980] 2002, Olshansky and Carnes 2001). Some official forecasters in countries belonging to the Organization for Economic Cooperation and Development (OECD) are also on this end of the spectrum.
Other official forecasters in the OECD believe that the speed of mortality decline will not be quite as rapid as in the past, but that there will still be a nonzero decline throughout the forecast period. This group includes the 2004 Social Security Trustees.
Demographers who extrapolate age-specific rates in mortality decline tend to believe that the speed of mortality decline will not slow down, relative to past performance (Lee and Carter 1992; Wilmoth 1998; Tuljapurkar, Li, and Boe 2000). (There are some exceptions, however; for example, the 1999 and 2003 Technical Panels slowed mortality decline at younger ages more than has occurred in the past. The 2003 Panel also set the ultimate rate of mortality decline to zero in 2200. The panel's use of a zero rate reflected an unwillingness to forecast farther into the future than the length of the observable past rather than a belief in a biological limit.)
Some forecasters predict even faster gains in life expectancy. Demographers who extrapolate linear increases in life expectancy tend to predict faster gains, in part because they rely more heavily on international trends to determine the U.S. forecast (White 2002, Oeppen and Vaupel 2002). Demographers who study healthy subpopulations believe that fairly large advances in life expectancy are achievable through modifications in behavior (Manton, Stallard, and Tolley 1991). Finally, researchers who believe that large medical breakthroughs are on the horizon forecast extremely large increases in life expectancy, relative to the predictions of other experts.
Introduction
The Social Security Trustees are responsible for projecting the finances of the Old-Age, Survivors, and Disability Insurance (OASDI) Trust Funds 75 years into the future. Mortality is one key demographic assumption that feeds into these long-range projections. The uncertainty that surrounds a 75-year mortality forecast is reflected in the fact that opinions about the appropriate speed of future mortality improvement vary in the literature.
Table 1 reflects the variance in opinion by providing a summary of period life expectancies at birth predicted by various experts in comparison with those of the Social Security Trustees' 2004 forecast.1 The estimates of maximum average and maximum achievable life expectancy are not directly comparable with the other forecasts in the table, but they are informative to the extent that they are or are not exceeded by the other forecasts.
| Expert | Forecasting technique | Period life expectancy at birth in calendar year |
Unisex | Male | Female |
|---|---|---|---|---|---|
| 2004 Social Security Trustees | Cause- and age-specific extrapolation | 2070 | 82.7 | 80.8 | 84.6 |
| 1999 Technical Panel (Lee) | Age-specific extrapolation | 2070 | 85.2 | . . . | . . . |
| 2003 Technical Panel (Wilmoth) | Age-specific extrapolation | 2070 | 84.4 | . . . | . . . |
| Lee and Miller (2001) | Age-specific extrapolation | 2075 | 86.2 | . . . | . . . |
| Lee and Carter (1992) | Age-specific extrapolation | 2065 | 86.05 | . . . | . . . |
| Oeppen and Vaupel (2002) | Linear convergence of life expectancies | 2070 | . . . | . . . | 92.5–101.5 |
| Fries (2003) | Maximum average life expectancy | 2076 | 87.8 | . . . | . . . |
| 2004 Social Security Trustees | Cause- and age-specific extrapolation | 2050 | 81.2 | 79.2 | 83.3 |
| Tuljapurkar, Li, and Boe (2000) | Age-specific extrapolation | 2050 | 82.91 | . . . | . . . |
| U.S. Census Bureau (2000) | Lee and Tuljapurkar stochastic model for 2065 combined with interpolation and targeting | 2050 | . . . | 81.2 | 86.7 |
| 2004 Social Security Trustees | Cause- and age-specific extrapolation | 2030 | 79.5 | 77.4 | 81.7 |
| White (2002) | Linear convergence of life expectancies | 2030 | 83.3 | . . . | . . . |
| Manton, Stallard, and Tolley (1991) | Maximum achievable life expectancy (optimal risk-factor interventions) | . . . | 95–100 | . . . | . . . |
| Olshansky and Carnes (2001) | Maximum average life expectancy | . . . | 85.0 | 81.2 | 88.0 |
| Fries (1980) | Maximum average life expectancy | . . . | 85.0 | . . . | . . . |
| SOURCE: Author's compilation. | |||||
| NOTES: The estimates of maximum achievable and maximum average life expectancy are not directly comparable with the other forecasts in the table. They are included so that readers can determine the extent to which the other year-specific forecasts do or do not exceed these estimates.
. . . = not applicable.
|
|||||
This review organizes the views of the experts presented in the table by
- comparing the Social Security Trustees' 2004 forecasts with the recommendations of the 1999 and 2003 Technical Panels on Assumptions and Methods,2
- examining the recommendations of researchers who use life-expectancy extrapolation techniques to forecast convergence in life expectancies among developed nations, and
- providing an overview of arguments in favor of a forecast that incorporates a theoretical maximum achievable life expectancy.
Comparison of the Trustees' Forecasts and the Technical Panels' Recommendations
The recommendations of the 1999 and 2003 Technical Panels were made by demographers Ron Lee and John Wilmoth, respectively. Both the Social Security Trustees and the two technical panels use a forecasting technique that involves the extrapolation of past trends. The technical panels project historical trends in age-specific mortality rates into the future using judgment to select the historical time period over which they make those projections. Judgment is also used in adopting the assumption that past trends in mortality by age will continue into the future (Van Hoorn and De Beer 2001, 218). In contrast, the Trustees project cause- and age-specific trends into the future using their judgment to adjust these trends to reflect a reasonable path of future mortality improvement. In this sense, the Trustees and the technical panels differ most fundamentally in the degree to which they believe that past mortality trends will continue unchanged into the long-term future and in their definitions of the relevant past.
Cause-Specific Forecasting
The 1999 Technical Panel stated in its report that "given our current state of knowledge, the best guides we have to the future are past trends and international experience" (p. 67). The panel pointed out that although there has been a major change in the structure of cause of death in the United States over the past century, the rate of mortality decline has been remarkably steady (p. 66).
The 2003 Panel made this view more explicit by recommending that the Trustees simplify their model by "dropping separate projections by cause of death and stating assumptions in terms of age-specific rates of decline for all-cause mortality" (p. 34). The panel asserted that projecting rates of mortality decline by cause of death is "unlikely to produce more accurate results, and there is little empirical basis for current assumptions" (p. 35). Citing Wilmoth (1995), the panel also notes that "over time categories that are assumed to decline the most slowly account for an increasing proportion of deaths" (p. 36), resulting in a deceleration in rates of mortality decline over the projection period. In contrast to the 2004 Trustees' assumption of a slow and steady deceleration continuing throughout the 75-year projection period and beyond, the 2003 Technical Panel assumed higher rates of mortality decline earlier in the projection period, reverting to a more pronounced deceleration from 2077 to a zero rate of decline in 2200 (Office of the Chief Actuary (OCACT) staff, Social Security Administration, personal communication, August 27, 2004).
Concerns about cause-specific death projections are not new. One concern is that such a technique assumes independence among causes of death, when in reality several causes often contribute simultaneously to death, particularly at older ages. In addition, historically, rates of decline for specific causes of death have varied more than have rates of decline for all-cause mortality (Technical Panel 2003, 38). Empirically, data on mortality by cause only begins in 1979—too short a time period for an indefinite ultimate forecast, according to the 2003 Panel (p. 38). Tabeau and others (2001) argue that the underlying cause of death is more difficult to identify at approximately ages 90 and older (p. 185) and suggest that a cause-of-death methodology is most useful for short-term forecasting and more risky for long-term forecasts (p. 186).
Note, however, that past Trustees have used their cause-of-death methodology to guide their projections rather than to determine them. The methodology serves as an important basis for analysis relative to past trends and for assessing the reasonableness of future assumptions, but it is not the sole factor used in setting mortality assumptions (OCACT staff, personal communication, August 27, 2004).
Trustees' Forecast in the Context of Other Official National Forecasts
The method used in the 2004 Trustees Report appears to fall within the mainstream of that used by official national forecasters in countries belonging to the Organization for Economic Cooperation and Development. The majority of these countries employ some combination of extrapolating past trends and using expert judgment in forecasting future mortality decline. The United Kingdom, Denmark, Finland, Ireland, and Spain apply a combination of extrapolation and targeting. The target is decided by expert opinion and best judgment, and rates are interpolated backward from the target (Cruijsen and Eding 2001, 242). Austria, Germany, the Netherlands, and Sweden tend to rely more heavily on setting feasible targets (Cruijsen and Eding 2001, 242) than the preceding group of countries, which use a heavier dose of extrapolation. Belgium, France, and Luxembourg extrapolate death rates using age-specific mathematical functions that best describe past changes but then correct them to avoid "non-plausible future age patterns or unrealistically low levels" (Cruijsen and Eding 2001, 242). Note that although France, Ireland, Italy, the Netherlands, and the United Kingdom all conduct fairly extensive reviews of their mortality assumptions (Cruijsen and Eding 2001, 241), the techniques they choose to adopt are not identical.
What unites these countries' techniques is that they all project "further improvements in life expectancy at birth but at a lower rate than that observed during the 1970s and 1980s" (Cruijsen and Eding 2001, 243).3 Thus, the Trustees lie within the mainstream of official forecasters in that "all [European] forecasters . . . use the basic assumption that improvements in survival rates will become increasingly difficult as life expectancy progresses" (Cruijsen and Eding 2001, 240).
In addition, several countries predict less mortality improvement than do the Trustees. Denmark and Finland assume that the trend in increasing life expectancy will stop in 2010 (Cruijsen and Eding 2001, 243). In addition, Denmark assumes that everyone dies by age 109; Germany assumes that all people who reach age 98 do not survive in the next calendar year (Cruijsen and Eding 2001, 230). The Netherlands performs an age-specific extrapolation in the short term but in the long term assumes that the survival curve will become more rectangular, that is, mortality rates at ages in midlife will decline more than mortality rates at the oldest ages, and therefore more people will become old but not even older (Van Hoorn and De Beer 2001, 219). This assumption is essentially a variation of the notion of a theoretical maximum average life expectancy.
The Government Actuary's Department of the United Kingdom recently conducted an extensive review of its mortality projection methodology. This review included testing its current method of historical extrapolation and targeting against various other methods of mortality projection, including a variant of the Lee–Carter method (the type of method used by the 1993 and 2003 Technical Panels). The Government Actuary's Department of the United Kingdom found that their current method outperformed the Lee–Carter method; specifically, they were better able to incorporate cohort differences using their method. (In the United Kingdom, historical data show that birth cohorts 1925 through 1945 have experienced greater levels of mortality decline than those born on either side of this period, but it is not known why these cohort effects have occurred (Gallop and Thompson 2003, 5).)
A review of mortality projections leads one to conclude that differences of opinion correspond to some extent to the area of professional training. For example, when the Society of Actuaries conducted a survey of 79 experts from Canada, Mexico, and the United States, actuaries and economists tended on average to project lower rates of mortality decline than did demographers, and demographers tended to have a greater spread (standard deviation) between their opinions (see Table 2).
| Profession | Number | Median | Mean | Standard deviation |
|---|---|---|---|---|
| Male | ||||
| Actuary | 29 | 0.60 | 0.64 | 0.24 |
| Demographer | 4 | 0.70 | 0.82 | 0.62 |
| Economist | 5 | 0.65 | 0.60 | 0.19 |
| Other | 3 | 0.70 | 0.80 | 0.17 |
| Female | ||||
| Actuary | 29 | 0.60 | 0.64 | 0.25 |
| Demographer | 4 | 0.80 | 0.93 | 0.70 |
| Economist | 5 | 0.65 | 0.60 | 0.19 |
| Other | 3 | 0.90 | 0.87 | 0.15 |
| SOURCE: Marjorie Rosenberg and Warren Luckner, "Summary of Results of Survey of Seminar Attendees," North American Actuarial Journal 2(4) (October): 75, Table 5 (1998). | ||||
Accuracy of the Trustees' Forecasts Over Time
Although the majority of official forecasters adjust their extrapolations by using expert judgment, this approach is not without its critics. A common critique of official forecasts is that the historical time period chosen to inform the long-term forecasts is frequently too short. For example, Wilmoth (1998) discusses the tendency for forecasters to react to short-term fluctuations in mortality rates. When the rate of mortality decline slowed in the 1950s and 1960s, many forecasters predicted that the rise in life expectancy was over (Wilmoth 1998, 395–396). When mortality declined rapidly after 1968, many predicted that rapid declines would continue indefinitely (p. 396). (Note that this general rule does not seem to apply to European forecasters who are slowing down their rates of mortality improvement in the future despite current rapid declines in mortality.)
Olshansky (1988) examined the accuracy of the Trustees' forecasts over time and came to a similar conclusion. He states that the Trustees underestimated the pace of mortality decline in the 1970s because they were extrapolating the slow pace of mortality decline of the 1950s and 1960s. He adds that in the first half of the 1980s, the Trustees overestimated the pace of mortality decline (particularly for females) because they were extrapolating the fast pace of mortality improvement of the 1970s. However, unlike Wilmoth, Olshansky concludes that this highlights a flaw in the use of extrapolation models rather than a flaw in the length of the time periods selected for extrapolation.
Lee and Miller (2001) compared the performance of the forecasts of the Lee–Carter age-extrapolation model with that of the Trustees' past forecasts. Beginning with 1945 as a jump-off year, they found that the Lee–Carter model tended to underpredict gains in life expectancy but always predicted a life-expectancy value for 1998 that was within 2 years of the actual life-expectancy value for 1998 (Lee and Miller 2001, 547).4 By comparing the divergence from actual values in their forecast starting in 1950 with the Trustees' forecasts starting in 1950, Lee and Miller conclude that "Social Security projections also have systematically underpredicted future gains in [life expectancy at birth] since 1950" (p. 547) but that the Trustees' divergence from actual life expectancy was greater than that of the Lee–Carter model.
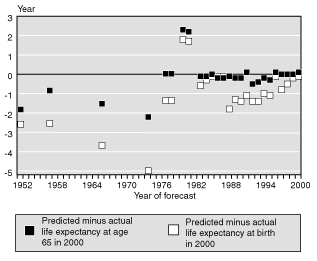
Lee and Miller (2001, 545) find systematic underprediction of gains in life expectancy by the Trustees when they give each decade since 1950 an equal weight; however, since 1980, the Trustees' forecasts have diverged much less from the actual value in 2000 than they did before 1980 (Chart 1). They have also not been consistently below the actual value since 1980. This situation can be seen in Chart 1, which shows the difference between past Trustees' forecasts of life expectancy and actual life expectancy in 2000.
Difference between past Social Security Trustees' forecasts of life expectancy and actual life expectancy for males and females, 2000
| Year | Male | Female | ||
|---|---|---|---|---|
| At age 65 in 2000 | At birth in 2000 | At age 65 in 2000 | At birth in 2000 | |
| 1952 | -1.8 | -2.6 | -3.0 | -3.9 |
| 1953 | -- | -- | -- | -- |
| 1954 | -- | -- | -- | -- |
| 1955 | -- | -- | -- | -- |
| 1956 | -- | -- | -- | -- |
| 1957 | -0.8 | -2.6 | -1.4 | -2.3 |
| 1958 | -- | -- | -- | -- |
| 1959 | -- | -- | -- | -- |
| 1960 | -- | -- | -- | -- |
| 1961 | -- | -- | -- | -- |
| 1962 | -- | -- | -- | -- |
| 1963 | -- | -- | -- | -- |
| 1964 | -- | -- | -- | -- |
| 1965 | -- | -- | -- | -- |
| 1966 | -1.5 | -3.7 | -2.2 | -3.0 |
| 1967 | -- | -- | -- | -- |
| 1968 | -- | -- | -- | -- |
| 1969 | -- | -- | -- | -- |
| 1970 | -- | -- | -- | -- |
| 1971 | -- | -- | -- | -- |
| 1972 | -- | -- | -- | -- |
| 1973 | -- | -- | -- | -- |
| 1974 | -2.2 | -5.0 | -0.8 | -2.5 |
| 1975 | -- | -- | -- | -- |
| 1976 | -- | -- | -- | -- |
| 1977 | -1.2 | -3.7 | 0.0 | -1.4 |
| 1978 | -1.2 | -3.7 | 0.0 | -1.4 |
| 1980 | -0.3 | -1.2 | 2.3 | 1.8 |
| 1981 | 0.0 | -1.1 | 2.2 | 1.7 |
| 1983 | -0.1 | -0.6 | 1.9 | 1.6 |
| 1984 | -0.1 | -0.3 | 1.9 | 1.7 |
| 1985 | 0.0 | -0.1 | 1.8 | 1.8 |
| 1986 | -0.2 | -0.1 | 1.4 | 1.6 |
| 1987 | -0.2 | -0.1 | 1.2 | 1.4 |
| 1988 | -0.1 | -1.8 | 0.9 | 0.8 |
| 1989 | -0.2 | -1.3 | 0.7 | 0.7 |
| 1990 | -0.2 | -1.4 | 0.6 | 0.5 |
| 1991 | 0.1 | -1.1 | 0.7 | 0.5 |
| 1992 | -0.5 | -1.4 | 0.4 | 0.3 |
| 1993 | -0.4 | -1.4 | 0.5 | 0.3 |
| 1994 | -0.2 | -1.0 | 0.5 | 0.3 |
| 1995 | -0.3 | -1.1 | 0.4 | 0.3 |
| 1996 | 0.1 | -0.1 | 0.6 | 0.8 |
| 1997 | 0.0 | -0.8 | 0.4 | 0.3 |
| 1998 | 0.0 | -0.5 | 0.4 | 0.2 |
| 1999 | 0.0 | -0.2 | 0.3 | 0.2 |
| 2000 | 0.1 | -0.1 | 0.3 | 0.2 |
| NOTE: -- = not available. | ||||
As Lee and Miller (2001) point out, without weighting, the longer-horizon forecasts would count for less than the shorter-horizon forecasts. On the one hand, long-term horizons are both harder to predict and more relevant to the debate over the Trustees' ultimate rates of mortality decline. On the other hand, it is difficult to know how to compare a forecast made in 1952—based on state-of-the-art knowledge at the time—with a forecast made more than 40 years later. In addition, the Trustees' forecasts of life expectancy at birth have tended to be farther from actual values than have their forecasts of life expectancy at age 65. Because the majority of deaths occur after age 65, the age-65 measure could be judged to be more relevant for the Social Security Trustees Report; however, the literature reviewed for this article more commonly describes mortality improvements in terms of life expectancy at birth.
Choice of a Historical Time Period for Extrapolation
With regard to the appropriate use of historical rates of mortality decline, there appears to be an essential difference in philosophy between the Trustees and the two technical panels. Because rates of mortality improvement have not been constant in the past, the assumptions in the Trustees Report reflect the belief that "it is crucial to study not only the differing historical rates of decline for various periods, but also the conditions that contributed to these variations. Only after considering how future conditions will differ from the past can [one] speculate about future mortality improvement" (OCACT staff, personal communication, August 27, 2004). In contrast, the two technical panels view variations in rates of mortality decline as more akin to statistical fluctuations around a long-term mean. However, as described in the following discussion, the two technical panels occasionally depart from a pure mathematical extrapolation exercise. In this sense, all three forecasts use some form of expert judgment rather than make the future extrapolations a perfect mirror of the past.
Both technical panels agreed with the Trustees that rates of mortality decline should be lower at young ages than the historical average over either the 1900–2000 or 1950–2000 time period because of a shift in the age pattern of decline at these young ages in both the United States and in "countries with low mortality (such as Japan, Sweden, and France)" (Technical Panel 1999, 66). However, the 2003 Technical Panel explicitly stated that the Trustees' deceleration at young ages was still too large and therefore recommended slowing the rate of deceleration (or raising the rate of mortality decline) at ages 0–14 and 15–64.5 Differences in rates of mortality decline for ages 64 and younger affect forecasts of life expectancy at birth but not those at age 65. Because the majority of deaths occur after age 65, rates of mortality decline at younger ages do not have a huge impact on calculations of life expectancy at birth but instead create slight differences.
Both technical panels agreed that the average rates of decline from 1950 to the present should guide the projections for older ages. However, the 2003 Technical Panel went further, explicitly recommending changes in the Trustees' forecasting technique that resulted in a recommended life expectancy at birth of 84.4 years in 2070. In contrast, the 1999 Technical Panel advised the Trustees to increase their ultimate rates of reduction by enough to hit a targeted life expectancy at birth of 85.2 years in 2070.
Thus, the two technical panels take different approaches in their recommendations to the Trustees for modeling the age pattern of mortality declines at older ages. The 1999 Technical Panel recommends maintaining the age distribution in rates of decline used by the Trustees. (The Trustees "compress" the rates of decline so that the rates are fairly similar across adult ages.) The 2003 Technical Panel assumes constant rates of mortality decline for ages 20 through 74, followed by a reduction in rates of mortality improvement after age 75, ending at a zero rate of improvement at age 120. This assumption more closely matches the observed data from 1950–2000.
Because of these differences in modeling the age pattern of mortality decline at older ages, the Trustees and the 1999 Technical Panel assume higher rates of improvement above age 95 than does the 2003 Technical Panel (OCACT staff, personal communication, August 27, 2004). The 2003 Technical Panel also phases in the convergence to the 2027–2077 rates of mortality decline faster than the 1999 Technical Panel and the Trustees. The 2003 Technical Panel forces convergence in 10 years, while the 1999 Technical Panel recommends that the Trustees maintain their current practice of allowing the rates of mortality decline to converge over 25 years. In addition, the 2003 Panel assumes a linear reduction in rates of decline (toward zero) beginning at the end of the ultimate period (2077) and ending in 2200. The idea is to "not assume positive rates of mortality decline farther into the future than has been observed in the past" (Technical Panel 2003, 40). The 1999 Technical Panel does not make a specific recommendation past the 75-year forecast horizon. The 2004 Trustees have their ultimate rates continue indefinitely.
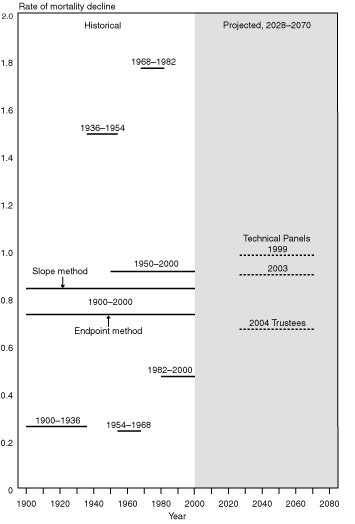
The result of these similarities and differences is that annual mortality reductions over the last 50 years of the projection period for ages 65 and older average 0.99 for the 1999 Technical Panel, 0.90 for the 2003 Technical Panel, and 0.68 for the 2004 Trustees (Technical Panel 2003, 37, Table 3). These reductions result in projected life expectancies at birth (in 2070) of 85.2, 84.4, and 82.7 years, respectively.6 Thus, the Trustees and the two technical panels project the annual percentage reduction in the mortality rate for ages 65 and older to increase from its 1982–2000 average of 0.47. The Trustees' forecast is fairly close to the 1900–2000 historical average but is still below it (see Chart 2 and Table 3). The 2003 Technical Panel's forecast matches the 1950–2000 historical average, and the 1999 Technical Panel's forecast is slightly above it. The greater height of the average for the 1950–2000 period compared with that of the 1900–2000 average in Chart 2 is partly explained by high rates of mortality improvement from 1968 through 1982.
Average annual reduction in unisex age-adjusted death rates for ages 65 and older, by historical and projected periods
| Time period | Unisex | Male | Female |
|---|---|---|---|
| Historical | |||
| 1900–1936 | 0.26 | 0.20 | 0.31 |
| 1936–1954 | 1.49 | 1.18 | 1.77 |
| 1954–1968 | 0.24 | -0.35 | 0.72 |
| 1968–1982 | 1.78 | 1.49 | 2.05 |
| 1982–2000 | 0.47 | 0.72 | 0.15 |
| 1950–2000 | 0.91 | . . . | . . . |
| 1900–2000 | . . . | 0.58 | 0.85 |
| 1900–2000, endpoint method | 0.73 | . . . | . . . |
| 1900–2000, slope method | 0.84 | . . . | . . . |
| Projected | |||
| 1999 Technical Panel (2023–2073) |
0.99 | . . . | . . . |
| 2003 Technical Panel (2027–2077) |
0.90 | . . . | . . . |
| 2004 Social Security Trustees (2028–2078) |
0.68 | 0.68 | 0.67 |
| SOURCES: Projected rates of the 1999 and 2003 Technical Panels and for the 1950–2000 series are from Technical Panel (2003, 37, Table 3). Wilmoth (2005) for the slope and endpoint methods, 1900–2000 series; and the Social Security Administration's Office of the Chief Actuary for all other historical and projected series. | |||
| NOTE: . . . = not applicable. | |||
Even a comparison of various forecasts with historical averages is not completely straightforward. The 2003 Technical Panel found that the mathematical method used to measure past rates of mortality decline can have a significant effect on the resulting historical average. For example, Wilmoth (2005) calculates the 1900–2000 unisex historical average using four different methods: the slope method results in an average of 0.84; the endpoint method, 0.73; an average of those two methods, 0.78; and the 5-slope average, 0.76. The slope and endpoint methods are highlighted in Chart 2 and Table 3 to allow a full comparison with the Trustees' 2004 forecast. In summary, the slope method fits a line to the historical data, while the endpoint method measures the decline between the beginning and the end of the time period (Technical Panel 2003, 37). Thus, the endpoint method results in a lower average because the end of the time period was one of relatively low rates of mortality decline. The 2003 Technical Panel chose to use an average of the slope and endpoint methods (0.78) for their forecasts.7
Note also that the unisex averages sometimes mask wide differences in rates of mortality decline between males and females, as seen in Table 3. The 2004 Trustees' ultimate rate is slightly closer to the average rate of mortality improvement for males than to the average rate for females over the 20th century. This ultimate rate represents the view implicit in the Trustees Report that average rates of mortality improvement for females will ultimately converge with those for males (OCACT staff, personal communication, August 27, 2004). In contrast, compared with historical data from the entire 20th century, the two technical panels could be said to have their rates of mortality decline for males converging towards those of females, in that their unisex rates of decline are closer to the average for females than to the average for males.8
Differing Interpretations of the Historical Data
Social Security's Office of the Chief Actuary treats both periods of high mortality improvement in the 20th century (the 1940s and the 1970s) as periods of structural change. It has concluded that 1936 through 1954 was a period in which "dramatic advances in the standard of living were achieved, and medical practice expanded, including the introduction of antibiotics" (OCACT staff, personal communication, August 27, 2004). From 1968 through 1982, "access to medical services was greatly expanded through Medicare and Medicaid for the old, frail, and disadvantaged, those who account for the vast majority of deaths in the population" (OCACT staff, personal communication, August 27, 2004). Lynch and Brown (2001, 93) call this a "unique period in U.S. history" and hypothesize that Medicare could have had a role in reducing mortality rates. Olshansky and Ault (1986, 360) note that "federal health care programs that began in the 1960s were targeted primarily at the elderly and poor segments of the population, and are thought to have contributed to mortality declines by reducing inequities in access to quality health care."9 In contrast, Wilmoth (1998, 395) views gains in longevity as a more steady stream of continuous progress as the "result of a complex array of changes (standards of living, public health, personal hygiene, medical care), with different factors playing major or minor roles in different time periods." He believes that "much of this decline can be attributed to the directed actions of individuals and institutions, whose conscious efforts to improve health and reduce mortality will continue in the future."
The question then becomes why the 1950–2000 period better represents expectations for the future than does the 1900–2000 period. The 2003 Technical Panel offers several justifications for their use of the second half of the 20th century. They note that the pace of mortality decline was more even across all ages over the 1950–2000 period than over the 1900–2000 period. They are also skeptical about the quality of mortality data, particularly at older ages, for the 1900–1950 period. Finally, both the 1999 and 2003 Technical Panels cite international comparisons as a guide to future mortality trends. Because the majority of developed countries have experienced more rapid mortality declines during the past 20 years, the panels believe that the United States is likely to recover from its slower rates, once the effects of female smoking on mortality work their way through the life table. White (2002) adds that infectious disease was an uncommon cause of death by 1950, while heart disease and cancer were the two most common causes, as they are today. This view seems to imply that the diseases affecting death rates from 1900 through 1950 are less applicable to expectations for the future than the dominant causes of death from 1950 through 2000.
On the other hand, official European forecasters appear to view the rapid mortality improvements of the past 20 years as a short-term fluctuation, because the majority forecast a slowdown in mortality improvement. Thus, what one views as a long-term trend versus a short-term fluctuation appears to be somewhat subjective. Is the rapid period of mortality improvement in the United States from 1968 through 1982 excessive, or is the rate of the 1982–2000 slowdown excessive? Similarly, is the rapid rate of mortality improvement from 1982 through 2000 for most of Europe excessive? For example, if one believes that expanded health care coverage contributed to mortality rate declines—as the Trustees implicitly assume in their mortality assumptions—then one might consider whether the more generous social welfare systems of European nations contributed to higher rates of mortality decline over the past 20 years. One might also consider whether such generosity is sustainable in the future, given the aging of Europe's population. This idea depends in part on the importance of significant cultural differences between the United States and Europe and Japan. Differences in immigration policies could also affect rates of mortality decline, depending on how influxes of immigrants affect average rates of mortality decline in various countries. There may also be differences in the inclusion of immigrants in national statistics across countries (that is, the guest worker phenomenon).
In addition, Himes (1994, 647–648) found that the age pattern of mortality for the white population of the United States was very different from that of Sweden and Japan because of higher mortality in the middle age range compared with the oldest age range. One explanation postulated for this difference is that the white population of the United States is more heterogeneous than that of other low-mortality populations because of wider differences in education, income, and access to health care; another explanation points to differences in ethnic composition between the older and younger populations. Both explanations could create a more "advantaged" group of old survivors in the United States than in the other low-mortality countries.
Convergence of Life Expectancies
Although the two technical panels used international mortality experience to guide their recommendations, some researchers have gone farther by incorporating international experience directly into their forecasts for the United States. In addition, in contrast to the two technical panels and the Trustees, these researchers extrapolate trends in life expectancy, rather than trends in age-specific death rates, into the future. Note, however, that the technique of extrapolating trends in life expectancy into the future does not by itself provide the details required to project the population, as is done in the Social Security Trustees Report, because population projections require death probabilities by age and sex. The life-expectancy projections reached by life-expectancy extrapolations could theoretically be achieved by numerous combinations of age and sex death probabilities, which in turn implies theoretically numerous population projections.
White (2002) compared the fit of linear changes in life expectancy at birth with age-specific (both logged and unlogged) linear changes in life expectancy and found that linear changes in life expectancy fit average changes in mortality over time better than age-specific death rates. He used mortality data from 1955 through 1991 for his research (because that was the time period available in his data set). He also found evidence for convergence to group-average life expectancy among a group of high-income countries over time. In general, the lower the starting level of life expectancy for an individual country, the faster the average change in life expectancy. A developed country's life expectancy relative to the group average at the time of prediction was an even more powerful statistical predictor.
Thus, White (2002, 67) favors extrapolating an individual country's life expectancy in the context of a model that measures convergence to average life expectancy among the group of high-income developed countries.10 He suggests that evidence of convergence among developed nations means that it may be dangerous to predict future life-expectancy trends for a specific country by only extrapolating from that country's own mortality experience. For example, he references Tuljapurkar, Li, and Boe's (2000) projections (using individual countries' mortality rates) in which the gap in life expectancy at birth between Japan and the United States widens to 8 years by 2050. White (pp. 67–68) believes that such a gap would be surprising, because it has not been observed since the 1950s in the seven leading industrial (G7) countries. The gap is also almost twice the size of the largest gap between G7 countries in the 1980s or 1990s. (In contrast, White's model predicts that the United States' rate of increase in life expectancy will speed up a little and that Japan's rate of increase will slow down.) In this way, White implicitly assumes that the United States' divergence from average life expectancy is a temporary stochastic fluctuation below the mean and that Japan's divergence is a temporary fluctuation above the mean.
Specifically, although noting that average life expectancy for the entire group of developed nations is more accurate in his model, White (2002, 69, 71) predicts that the rate of increase in U.S. life expectancy at birth will rise from 0.16 per year to 0.21 per year, for a life expectancy at birth of 83.3 in 2030. He notes that this result is about 1.5 years above the Lee–Carter (1992) forecast. White's forecast is also 3.75 years above the 2004 forecast of the Social Security Trustees.
Oeppen and Vaupel (2002) also extrapolate from a linear life-expectancy trend; however, they measure what they call "best practice life expectancy." The best-practice life-expectancy concept refers to the highest recorded average life expectancy at birth in the world (by sex) for each year from 1840 to the present. "The gap between the record [highest life expectancy] and the national level is a measure of how much better a country might do at current states of knowledge and demonstrated practice" (Oeppen and Vaupel 2002, 1029). Oeppen and Vaupel (p. 1031) find that record female life expectancy has increased linearly by about 2.5 years per decade for the past 150 years (or by 0.25 per year). If the trend continues, they predict that female record life expectancy will be 100 in about 60 years (that is, around 2060).
Oeppen and Vaupel then forecast U.S. female life expectancy by measuring the gap between U.S. life expectancy and record life expectancy. Because the gap ranged from 10 years in 1900 to less than a year in 1950 to 5 years in 2000, they forecast U.S. female life expectancy to be between 92.5 and 101.5 years in 2070. (Their forecast is from 7.9 to 16.9 years higher than that of the 2004 Trustees.)
Lee (2003) combines the ideas of White (2002) and Oeppen and Vaupel (2002) by using the Human Mortality Database to estimate convergence toward record life expectancy among 18 countries with low mortality. He finds that countries tend to converge toward the life-expectancy leader (p. 5) and to converge more than proportionately with the size of the gap between their life expectancy and record life expectancy (p. 6). This finding is similar to that of White (2002), who found that a lower starting level of life expectancy for an individual country resulted in a faster average change in life expectancy.11 Lee (2003, 7) also suggests an extension to the model that "takes into account the heterogeneity of international experience, by incorporating additional factors that influence the level toward which each country's [life expectancy at birth] converges, which may not be the best practice level." That type of model could include such variables as "per capita income, educational attainment, nutritional measures, dietary measures, smoking behavior, and geographic/climatic conditions" (p. 7). It would allow countries to converge to different levels of life expectancy, although presumably their rate of improvement should then proceed in parallel, at the same rate. Thus, in contrast to White's model, this model in the United States would not necessarily converge toward the average level of life expectancy for high-income, low-mortality countries.
Theoretical Fixed Limits to Longevity
The idea of a linear trend in life expectancy continuing into the future is perhaps most diametrically the opposite of the idea of morbidity and mortality compression proposed by Fries ([1980], 2002). Fries proposed that the average age of onset of morbidity (poor health) will increase more than the average age of death as health improvements compress against the fixed limits of the human life span or human senescence (that is, the biological limits of the human body). Extrapolation techniques that project constant percentage increases in life expectancy into the future implicitly assume the potential for life expectancy to be infinite (Fries 1989, 221–222). In other words, these models do not explicitly rule out immortality, by not placing an upper bound on increases in longevity.12 In contrast, Fries (2002) estimates a maximum average life expectancy, under the assumption that it is "highly unlikely" that a medical breakthrough will be able to slow the human aging process in "our lifetime."
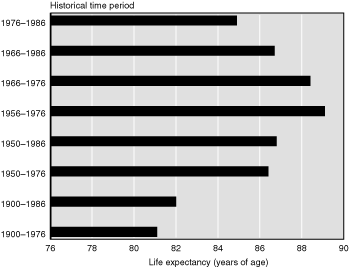
Fries (1989) calculates a maximum average life expectancy by estimating where the trend in average expected age of death from birth and the trend in average expected age of death at age 65 intersect. Fries calls the intersection the "point of paradox," because at the point of intersection there would be no deaths below age 65; that is, for life expectancy at birth to pass the intersection, there would have to be negative deaths, an impossibility. As Fries's sensitivity analysis shows (Chart 3), the point of intersection is dependent on the rate of mortality improvement at birth in relation to the rate at age 65. Thus, using historical data from 1900 through 1976 results in a lower maximum age (81.1), because the rate of improvement at birth is much faster than the rate of improvement at age 65. Using historical data from 1956 through 1976 results in a higher maximum age (89.1), because the rate of mortality improvement at birth has slowed down while the rate at age 65 has sped up (Chart 3). In this way, Fries faces the same decision as the two technical panels and the Trustees in deciding which time period is the most appropriate input for the projection. Fries's (1989, 221) interpretation of the rapid decreases in mortality rates of the 1970s appears more similar to that of the Trustees than to those of the two technical panels, in that he states:
It seems likely to this author, based on randomized controlled trial observations which suggest what might be possible as well as the current plateau in longevity gains, that we will never again see the rates of growth in life expectancy at advanced ages that occurred during the years of major decline in chronic vascular disease in the 1970s, except perhaps in certain disadvantaged subgroups.
Projections of maximum unisex average life expectancy, calculated using various historical time periods
| Historical time period | Life expectancy (years of age) |
|---|---|
| 1900–1976 | 81.1 |
| 1900–1986 | 82.0 |
| 1950–1976 | 86.4 |
| 1950–1986 | 86.8 |
| 1956–1976 | 89.1 |
| 1966–1976 | 88.4 |
| 1966–1986 | 86.7 |
| 1976–1986 | 84.9 |
Fries's (2003) most recent estimate of maximum average life expectancy at birth is 87.8 in 2076. Note that this represents a maximum and thus is a type of upper-bound estimate, not directly comparable with the projections discussed previously. Fries (1989) does not really believe that the rate of increase in life expectancy is perfectly linear, although he assumes linearity to calculate a maximum. Thus, he views his estimates as conservative, in that he suspects that the true maximum average life expectancy is below his estimate. However, Fries's estimate is informative to the extent that estimates of other researchers are higher. Only Oeppen and Vaupel's (2002) projection is higher, but it is limited to females whereas Fries's projection includes both males and females. Several more recent projections (Technical Panel 1999, Lee and Carter 1992, Lee and Miller 2001) exceed Fries's 1980 unisex estimate of 85 years of age, however.
Fries (1989, 2003) finds evidence for his compression theory in the results of randomized controlled trials in which preventive health interventions have reduced morbidity far more than they have reduced mortality and in the greater declines in disability rates than in mortality rates in the past 20 years. Others dispute that mortality is compressing toward a maximum average limit, primarily by measuring variability in age of death over time (Myers and Manton 1984, Wilmoth and Horiuchi 1999).
Manton, Stallard, and Tolley (1991) study natural populations with healthier-than-average lifestyles to determine whether there are natural populations whose life expectancies exceed those predicted by maximum average life-expectancy models like Fries's. This approach could be described as a calculation of a maximum achievable life expectancy—obviously these selective subgroups do not represent a nationwide average per se. Average life expectancy in these healthy subpopulations was as high as 97.4 at birth and 99.8 at age 65 for males and 98.1 at birth and 100 at age 65 for females. These high life expectancies are the result of standardized mortality ratios observed in healthy subpopulations that are much lower than those in the 1986 U.S. Census Bureau life table.
Manton, Stallard, and Tolley also calculate a theoretical limit to life expectancy, which assumes there is "optimal control" of risk factors, by running a simulation model that allows risk factors to vary over time and by age. (Note that, with the exception of smoking, the risk factors they model are physical factors like blood glucose and body mass index, not behavioral factors such as amount of exercise, nutrition, and physical activity, which apply to their study of natural populations. However, the risk factors they model are influenced by behaviors, although the extent of the influence could vary among individuals.) They apply their simulation model to the longitudinal (1950–1984) Framingham (Massachusetts) Heart Study and calculate a life expectancy limit at age 65 of 101.3 for males and 104 for females. Their estimate of unisex life expectancy at birth is from 95 to 100 years with a standard deviation of 10 years (Manton, Stallard, and Tolley 1991, 628). They believe that these estimates are "conservative" and that actual limits could be higher (p. 622).
Manton, Stallard, and Tolley are estimating a type of best achievable average life expectancy (without a projection date) rather than a predicted average life expectancy that could be used for cost estimates. Therefore, their estimates are not directly comparable with other projections. However, their estimates are informative to the extent that forecasters project over their maximum age limit. Although no 75-year forecast is currently above their maximum estimate, Oeppen and Vaupel's projection of female life expectancy at birth (92.5 to 101.5 in 2070) is close to the current maximum achievable average at birth for healthy natural female populations in the United States. This result might imply that the average U.S. lifestyle would have to become healthier for Oeppen and Vaupel's predictions to come true—barring an unforeseen medical breakthrough that could substitute for a shift to more healthy behaviors.
Olshansky and Carnes (2001) believe that using healthy populations to estimate maximum achievable life expectancy tends to overestimate likely maximums. They predict a maximum unisex average life expectancy at birth of age 85. They do not specify how they decide on age 85, but reading Olshansky and others (1990) suggests that the age is adopted from the work of Fries ([1980], 2002). Olshansky and Carnes (2001, 94–95) are skeptical of models based on healthy populations, because some studies find that healthy lifestyles reduce morbidity more than mortality and because Olshansky and Carnes believe that increases in life expectancy derived from lifestyle modification would not affect genetically unique individuals equally. Conceptually, this view could be equivalent to charging selection bias in models of maximum achievable average life expectancy—that is, healthy subpopulations may be genetically different from average. Selection bias would imply that even if the entire U.S. population adopted the lifestyle practices of the healthiest natural subpopulation group, their life expectancy would not necessarily increase to the subpopulation mean.13
Olshansky and Carnes also believe that age-specific extrapolation models tend to overestimate future gains in life expectancy by assuming that the future will resemble the past. Rather, Olshansky and Carnes believe that gains in life expectancy are harder to achieve at older ages than at younger ages because of the biological aging processes of the human body. Thus, they believe that the rapid gains of the past are unlikely to continue in the future. They also suggest that persons observed at ages 85 and older over the past 20 years are a "highly selected subgroup of hearty survivors" (Olshansky and Carnes 2001, 178). According to Olshansky and Carnes, because members of that subgroup survived major flu epidemics, the Great Depression, World Wars I and II, diseases like polio and diphtheria, poorer nutrition, and high rates of cigarette smoking, they may be selectively more robust than those of future cohorts, which will not have faced such weeding-out episodes. Olshansky and Carnes believe that it may be too risky to project from the experiences of such a select group.
For these reasons, Olshansky, Carnes, and Cassel (1990) believe that projections of life expectancy that exceed 85 years assume unrealistic declines in mortality. They calculate (using 1985 life tables) that mortality rates from all causes of death would have to decline by 55 percent at all ages and by 60 percent at ages 50 and older to achieve a life expectancy of age 85. Because they calculate that a 75 percent reduction in all-cause mortality would be equivalent to eliminating all deaths due to circulatory disease, cancer, and diabetes in 1985, they conclude that projections of life expectancy over age 85 do not meet the test of reasonableness. Other researchers such as Wilmoth (2001, 797) believe that such a judgment represents an implicit assumption of an absence of medical progress into the future and prefer to implicitly assume that medical progress will continue into the future in their projections.
Conclusion
As this literature review indicates, there are many different methods for projecting long-term mortality rates, none of which are universally accepted by all forecasters. Also evident is that the number of experts outside national governments who forecast time-specific mortality declines 75 years into the future is quite small. In general, the predictions of future mortality declines in the 2004 Social Security Trustees Report tend to be in the mainstream of professional actuarial and international official government opinion and to be lower than the majority of the small group of demographers who produce comparable estimates.
Notes
1. The Social Security Trustees' 2004 forecasts discussed in this review refer to forecasts based on their intermediate assumptions, which "reflect the Trustees' best estimates of future experience" (Board of Trustees 2004, 6). The Trustees also produce a low-cost and a high-cost set of assumptions to "provide a range of possible future experience" (p. 6). The low and high forecasts are not included in this review.
2. The 1999 and 2003 Technical Panels were appointed by the Social Security Advisory Board and were charged with reviewing the assumptions and methods used by the Social Security Trustees to project the future financial status of the Old-Age, Survivors, and Disability Insurance Trust Funds (Technical Panel on Assumptions and Methods 1999, 2003).
3. Both Statistics Canada and the U.S. Census Bureau are an exception to this general rule. For their long-term forecasts, they use some variant of the Lee–Carter model, which does not forecast a slowdown in age-specific rates of mortality decline. However, the national Canadian Pension Plan (CPP) adjusts its ultimate rates of mortality improvement to the projections of the Social Security Trustees (Government Actuary's Department 2001, 71–74).
4. The jump-off year refers to the year in which Lee and Miller begin extrapolating from historical data.
5. The 2003 Technical Panel recommended rates of mortality decline from 2027–2077 of 2.29 at ages 0–14 and 1.11 at ages 15–64, while the 2004 Trustees assumed rates of 1.55 and 0.78, respectively. The 1999 Technical Panel recommended rates of mortality decline from 2023–2077 of 2.23 at ages 0–14 and 1.13 at ages 15–64. The historical average from 1950–2000 was 2.90 at ages 0–14 and 1.22 at ages 15–64. Historical averages from 1900–1950 and 1900–2000 were higher (Technical Panel 2003, 37, Table 3).
6. Age-adjusted central death rates measure the number of deaths for a given population adjusted for the age composition of the given population. A rate of mortality decline measures the average annual decrease in the age-adjusted central death rate for a given age group. Thus, a higher annual rate of mortality reduction implies fewer deaths than a lower annual rate, and a negative rate of mortality reduction implies an increase in age-adjusted central death rates.
7. The 1950–2000 historical average in Chart 2 and Table 3 is an average of the slope and endpoint methods calculated by the 2003 Technical Panel (p. 37, Table 3).
8. Unisex averages for 1900–2000 in Chart 2 represent the slope and endpoint methods, calculated by the 2003 Technical Panel, whereas the male and female averages in Table 3 are calculated by the Social Security Administration's Office of the Chief Actuary. However, the difference between the slope and endpoint methods was 0.11, and the difference between the male and female averages was 0.27; that difference is large enough that this observation is unlikely to be reversed by any differences in calculation methods between the Office of the Chief Actuary and the 2003 Technical Panel.
9. In contrast, the 1999 and 2003 Technical Panels both assert that it is more likely that the United States is different from other countries in terms of levels of mortality rather than rates of mortality decline. Olshansky and Ault appear to be implying that inequalities in access to and quality of health care can affect average rates of mortality decline.
10. One might wonder about the selection criteria for the group of countries to include in the group average. White conducted sensitivity tests by excluding Greece, Ireland, Portugal, and Spain (countries whose gross domestic product at midperiod (1970) was less than half that of the wealthiest nation in 1970) without substantial differences in results. The full group of countries in his data set were Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany (West), Greece, Ireland, Italy, Japan, the Netherlands, New Zealand, Norway, Portugal, Spain, Sweden, Switzerland, the United Kingdom, and the United States.
11. As noted by White (2002), these findings could have implications for a country like Japan, whose official national forecasters predict slower gains in life expectancy than do forecasters extrapolating from Japan's age-specific rates of decline. Japan was more than 6 years below the life-expectancy leader (Norway) in 1955 (White 2002, Figure 3) and was the life-expectancy leader in 2000 (Oeppen and Vaupel 2002).
12. This criticism does not necessarily apply to the 2003 Technical Panel. Recall that the panel slows down rates of mortality decline to zero in 2200, although out of reluctance to project no farther into the future than the length of the observable historical time period rather than out of a conviction that there is a biological limit to human life expectancy.
13. Some of the healthy subpopulations that have been studied are better educated than the nationwide average. If socioeconomic status and inequality matters for mortality outcomes, raising the average level of life expectancy for the total population to that of these subpopulations could also require changes in the distribution of education and earnings among the total population. In addition, individuals in these studies who are of low socioeconomic status with healthy behaviors may be less representative of their subgroup means than are individuals of high socioeconomic status. As a result, controlling for socioeconomic status in these studies may not totally eliminate bias.
References
Board of Trustees of the Federal Old-Age and Survivors Insurance and Disability Insurance Trust Funds. 2004. 2004 Annual Report. Washington, DC.
Cruijsen, Harri, and Harold Eding. 2001. "The Latest Mortality Forecasts in the European Union." In Forecasting Mortality in Developed Countries: Insights from a Statistical, Demographic, and Epidemiological Perspective, edited by Ewa Tabeau, Anneke van den Berg Jeths, and Christopher Heathcote, 227–258. Boston: Kluwer Academic Publishers.
Fries, James F. 1980: "Aging, Natural Death, and the Compression of Morbidity." New England Journal of Medicine 303 (July 17): 130–135.
__________. 1989. "The Compression of Morbidity: Near or Far?" The Milbank Quarterly 67(2): 208–232.
__________. [1980] 2002. "Aging, Natural Death, and the Compression of Morbidity." Bulletin of the World Health Organization 80(3): 245–250 (WHO, Geneva, Switzerland).
__________. 2003. "Measuring and Monitoring Success in Compressing Morbidity." Annals of Internal Medicine 139 (5, pt. 2) (September): 455–459.
Gallop, Adrian, and James Thompson. 2003. "Mortality Measurement and Projections: Mortality Projections in the United Kingdom." International Social Security Association, Fourteenth International Conference of Social Security Actuaries and Statisticians, Mexico City (September).
Government Actuary's Department. 2001. "National Population Projections: Review of Methodology for Projecting Mortality." National Statistics Quality Review Series, No. 8.
Himes, Christine L. 1994. "Age Patterns of Mortality and Cause-of-Death Structures in Sweden, Japan, and the United States." Demography 31(4) (November): 633–650.
Lee, Ronald D. 2003. Mortality Forecasts and Linear Life Expectancy Trends. CEDA Papers. Berkeley: University of California, Center for the Economics and Demography of Aging. Available at http://repositories.cdlib.org/iber/ceda/papers/2003-0003CL.
Lee, Ronald D., and Lawrence R. Carter. 1992. "Modeling and Forecasting U.S. Mortality." Journal of the American Statistical Association 87(419) (September): 659–671.
Lee, Ronald D., and Timothy Miller. 2001. "Evaluating the Performance of the Lee–Carter Method for Forecasting Mortality." Demography 38(4) (November): 537–549.
Lynch, Scott M., and J. Scott Brown. 2001. "Reconsidering Mortality Compression and Deceleration: An Alternative Model of Mortality Rates." Demography 38(1) (February): 79–95.
Manton, Kenneth G., Eric Stallard, and H. Dennis Tolley. 1991. "Limits to Human Life Expectancy: Evidence, Prospects, and Implications." Population and Development Review 17(4) (December): 603–637.
Myers, George C., and Kenneth G. Manton. 1984. "Compression of Mortality: Myth or Reality?" The Gerontologist 24(4) (August): 346–353.
Olshansky, S. Jay. 1988. "On Forecasting Mortality." The Milbank Quarterly 66(3): 482–530.
Olshansky, S. Jay, and A. Brian Ault. 1986. "The Fourth Stage of the Epidemiologic Transition: The Age of the Delayed Degenerative Diseases." The Milbank Quarterly 64(3): 355–391.
Olshansky, S. Jay, Bruce A. Carnes, and Christine Cassel. 1990. "In Search of Methuselah: Estimating the Upper Limits to Human Longevity." Science 250(4981) (November): 634–640.
Olshansky, S. Jay, and Bruce A. Carnes. 2001. The Quest for Immortality. New York: W.W. Norton & Company.
Oeppen, Jim, and James W. Vaupel. 2002. "Broken Limits to Life Expectancy." Science 296 (May): 1029–1031.
Rosenberg, Marjorie, and Warren Luckner. 1998. "Summary of Results of Survey of Seminar Attendees." North American Actuarial Journal 2(4) (October): 64–82.
Tabeau, Ewa, Peter Ekampr, Corina Huisman, and Alinda Bosch. 2001. "Predicting Mortality from Period, Cohort or Cause-Specific Trends: A Study of Four European Countries." In Forecasting Mortality in Developed Countries: Insights from a Statistical, Demographic, and Epidemiological Perspective, edited by Ewa Tabeau, Anneke van den Berg Jeths, and Christopher Heathcote, 159–187. Boston: Kluwer Academic Publishers.
Technical Panel on Assumptions and Methods. 1999. Report to the Social Security Advisory Board. Washington, DC (November).
__________. 2003. Report to the Social Security Advisory Board. Washington, DC (October).
Tuljapurkar, Shripad, Nan Li, and Carl Boe. 2000. "A Universal Pattern of Mortality Decline in the G7 Countries." Nature 405 (June): 789–792.
U.S. Census Bureau. 2000. Methodology and Assumptions for the Population Projections of the United States: 1999 to 2100 (Working Paper No. 38), by Frederick W. Hollmann, Tammany J. Mulder, and Jeffrey E. Kallan. Washington, DC: Population Projections Branch, Population Division (January). Available at http://www.census.gov/population/www/documentation/twps0038.html.
Van Hoorn, Wim, and Joop de Beer. 2001. "Projecting Mortality in Population Forecasts in the Netherlands." In Forecasting Mortality in Developed Countries: Insights from a Statistical, Demographic, and Epidemiological Perspective, edited by Ewa Tabeau, Anneke van den Berg Jeths, and Christopher Heathcote, 205–226. Boston: Kluwer Academic Publishers.
White, Kevin M. 2002. "Longevity Advances in High-Income Countries, 1955–96." Population and Development Review 28(1) (March): 59–76.
Wilmoth, John R. 1995. "Are Mortality Projections Always More Pessimistic When Disaggregated by Cause of Death?" Mathematical Population Studies 5(4): 293–319, as cited in Technical Panel on Assumptions and Methods (2003), Report to the Social Security Advisory Board, Washington, DC (October).
__________. 1998. "The Future of Human Longevity: A Demographer's Perspective." Science 280 (April): 395–397.
__________. 2001. "How Long Can we Live? A Review Essay." Population and Development Review 27(4) (December): 719–800.
__________. 2005. "Overview and Discussion of the Social Security Mortality Projections." Working Paper, Social Security Advisory Board (May).
Wilmoth, John R., and Shiro Horiuchi. 1999. "Rectangularization Revisited: Variability of Age at Death Within Human Populations." Demography 36(4) (November): 475–495.